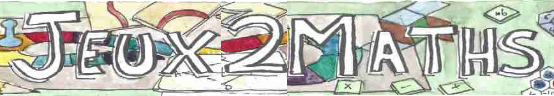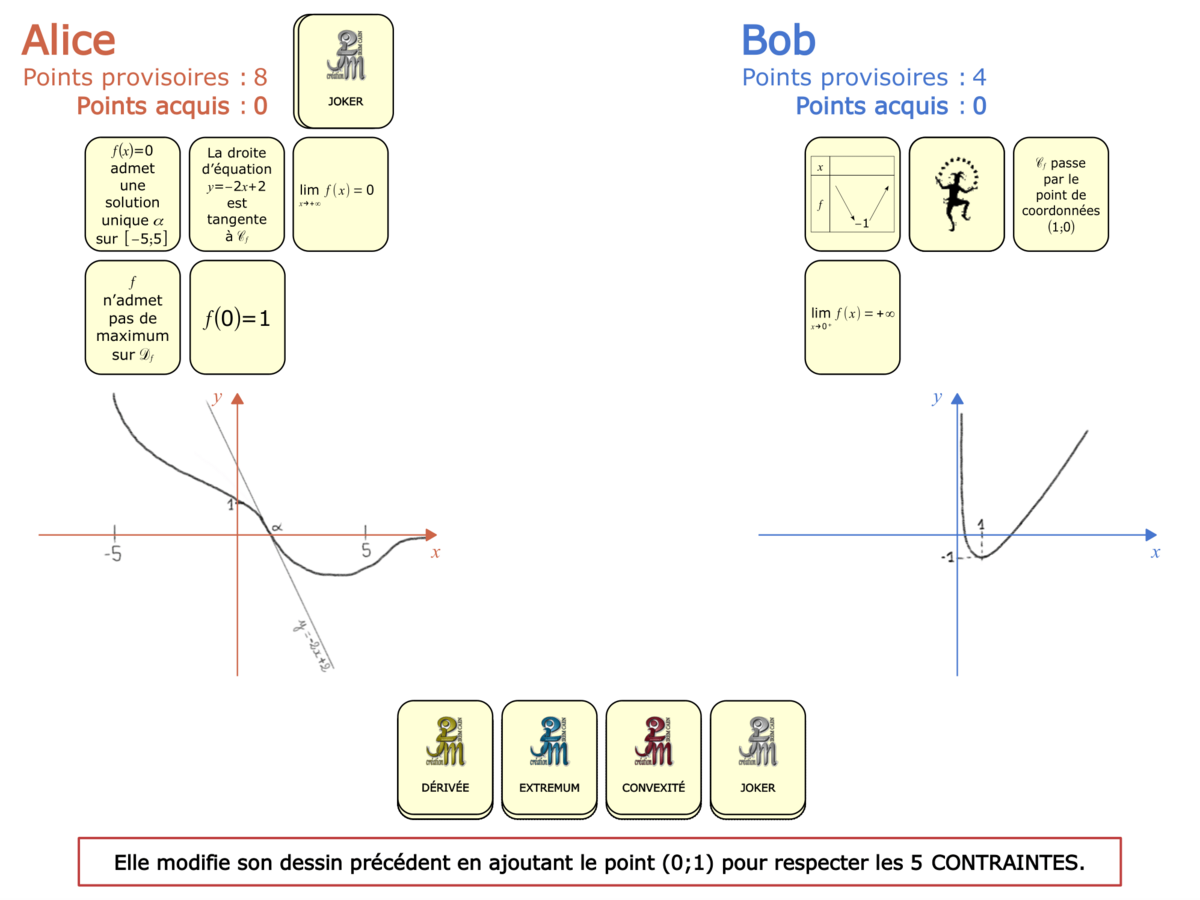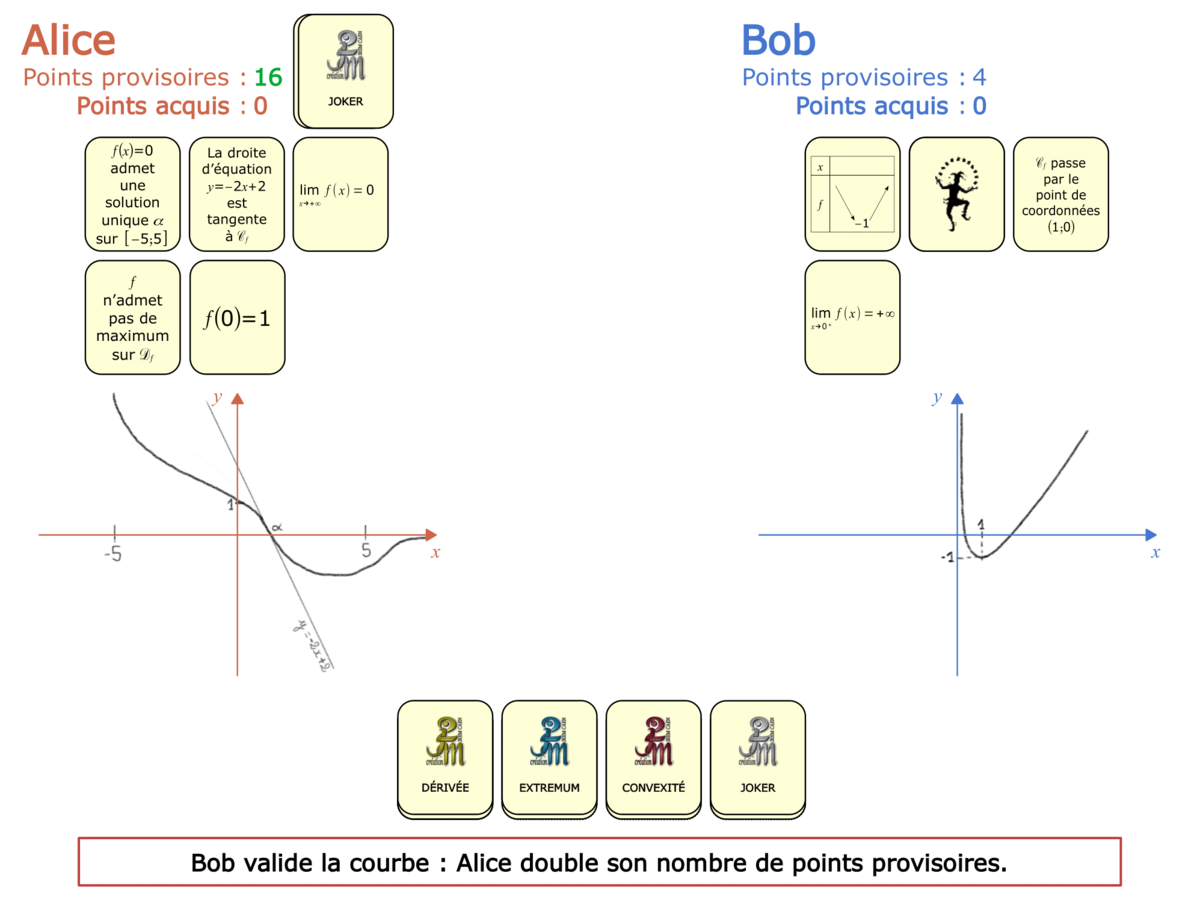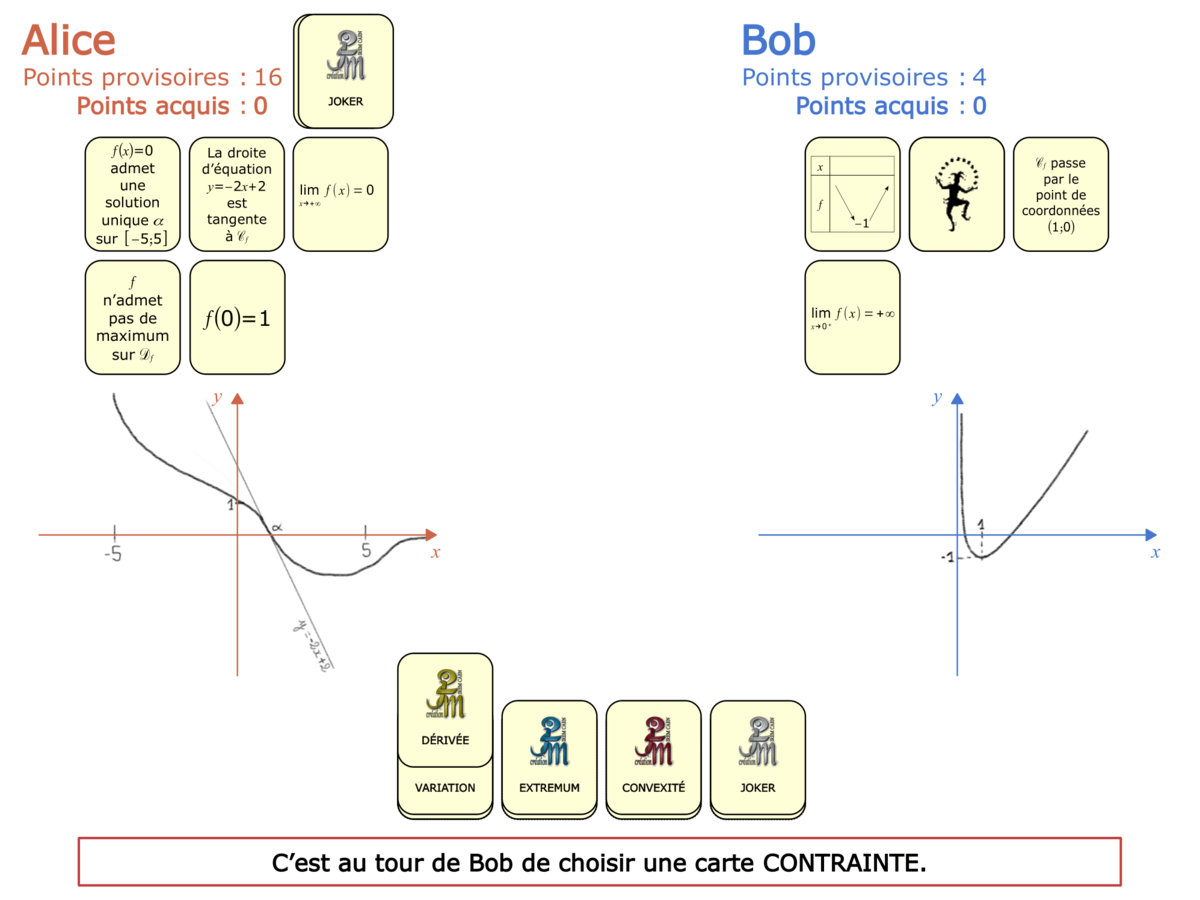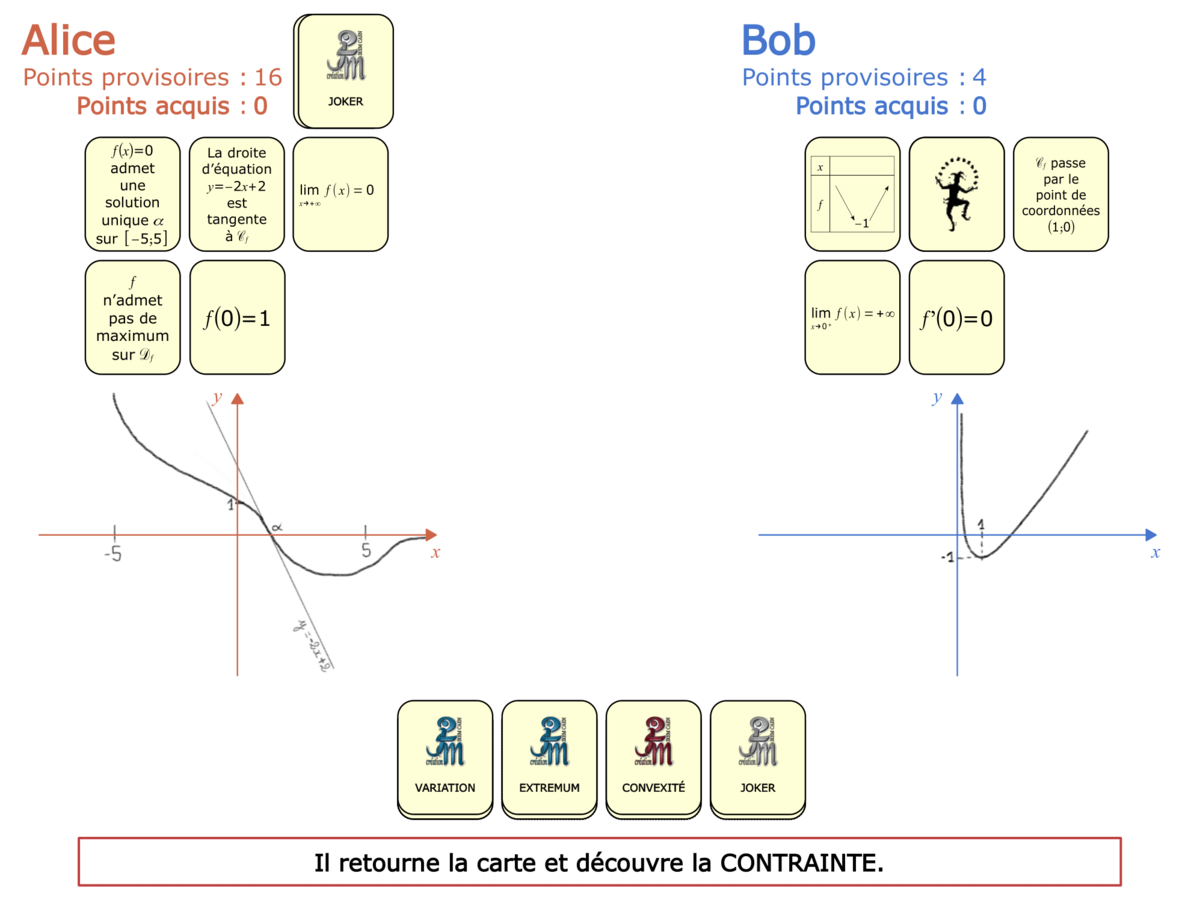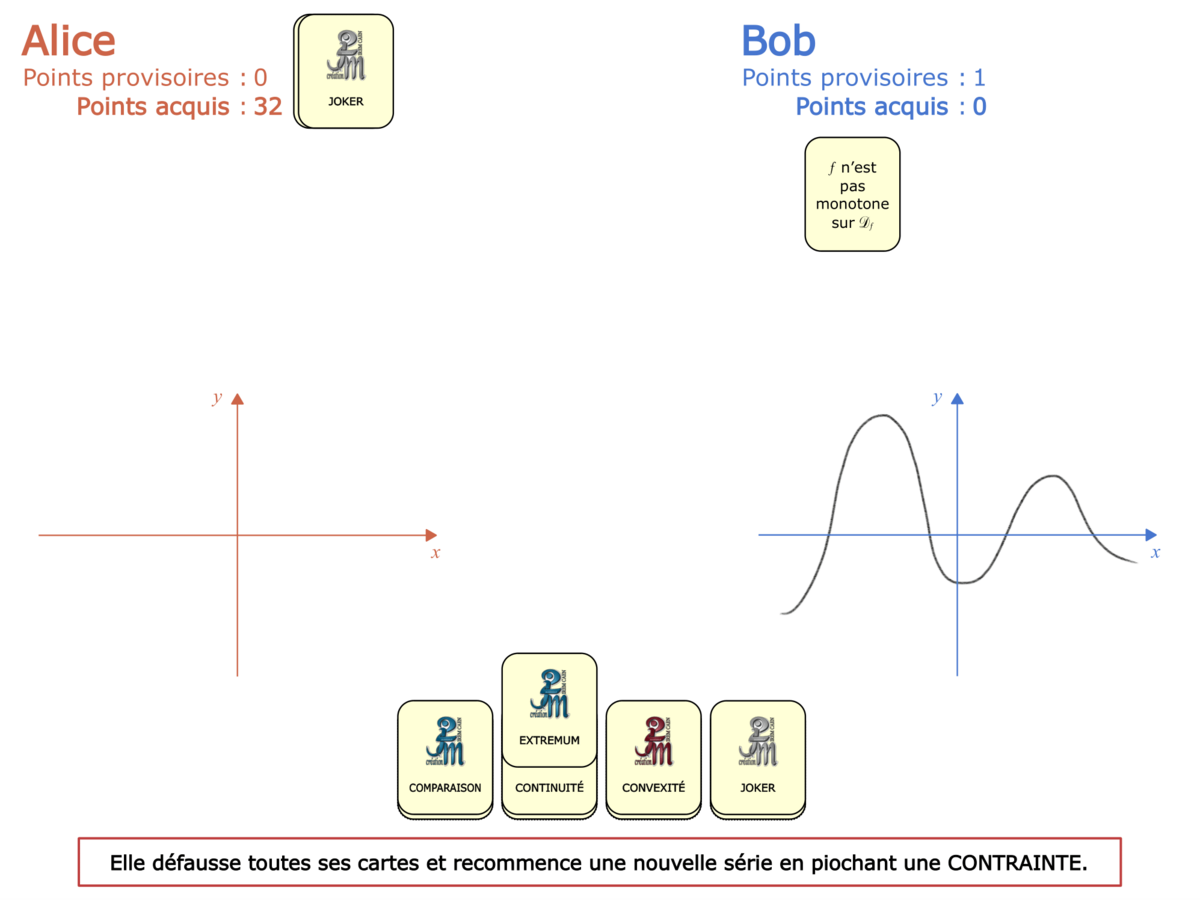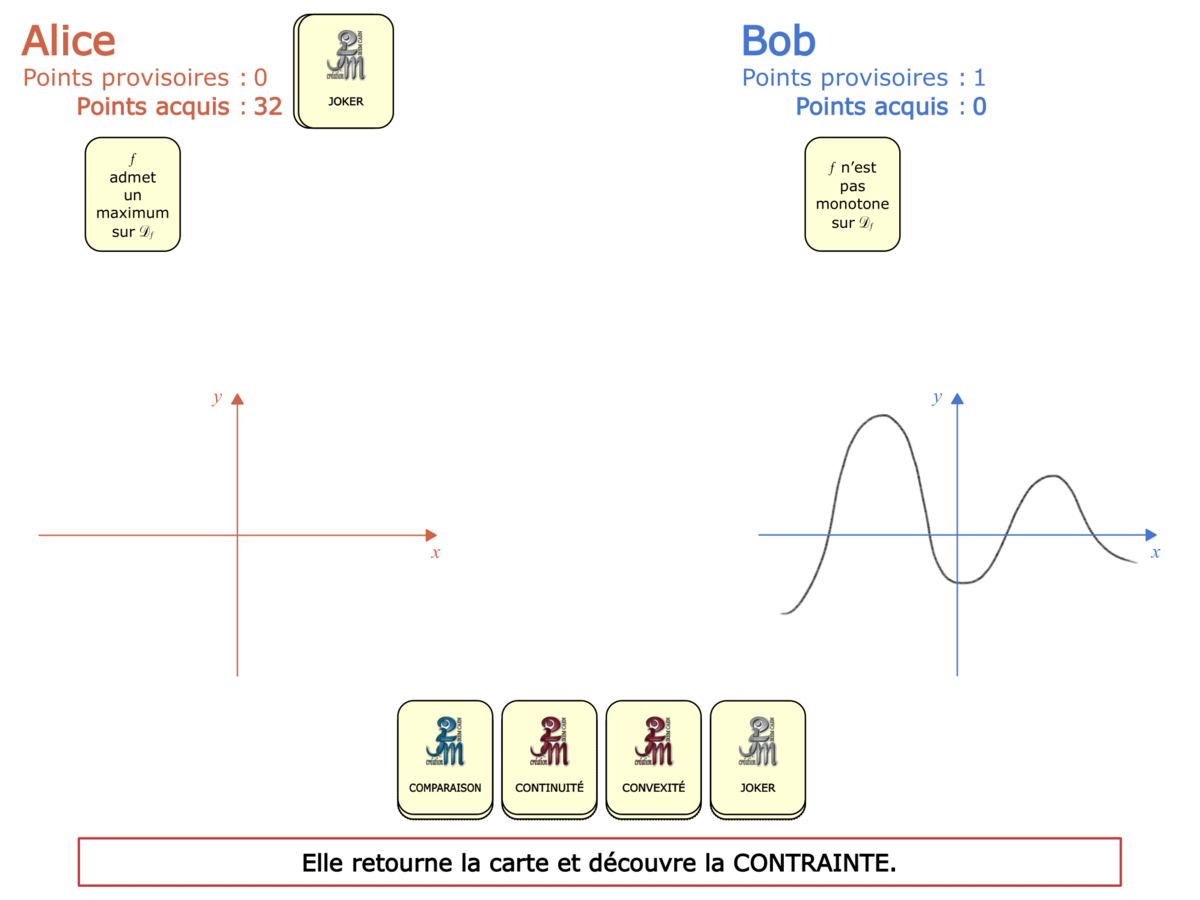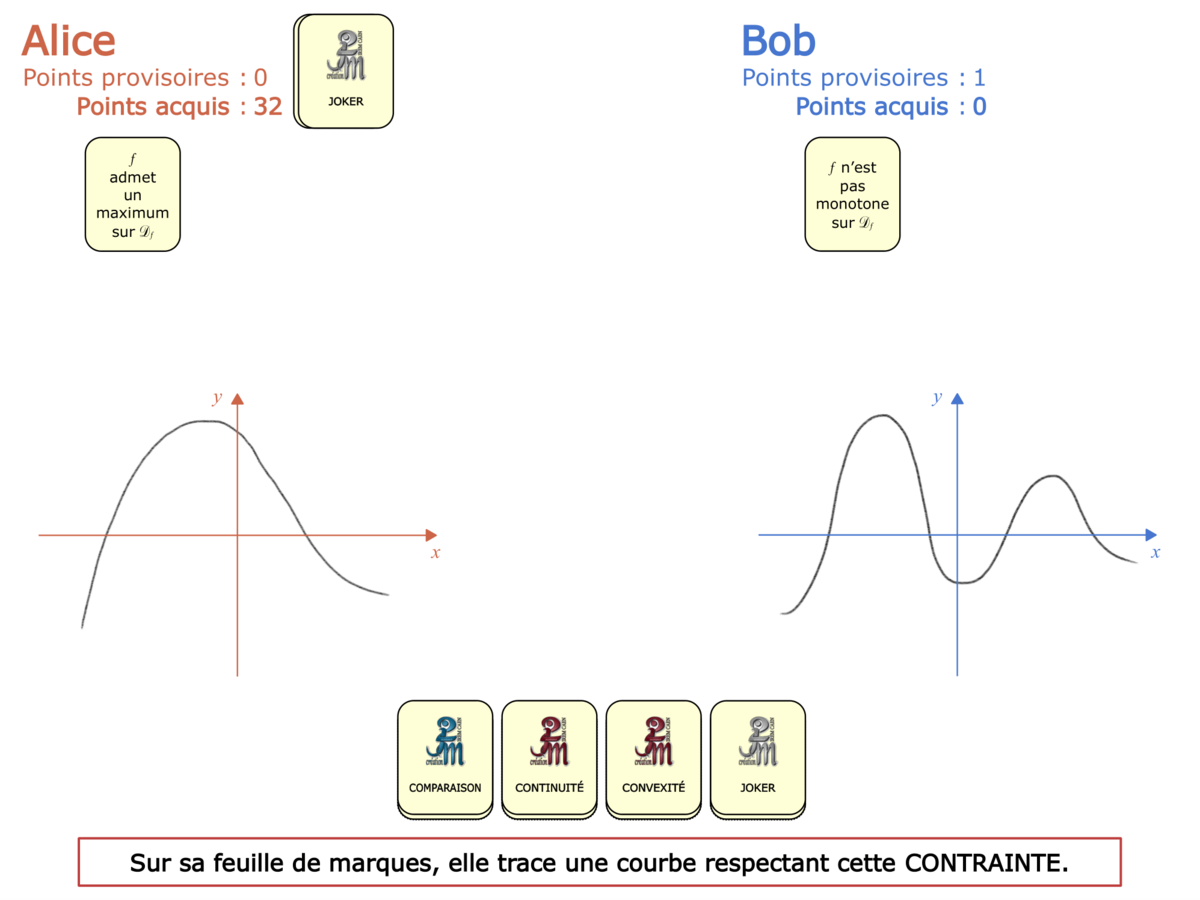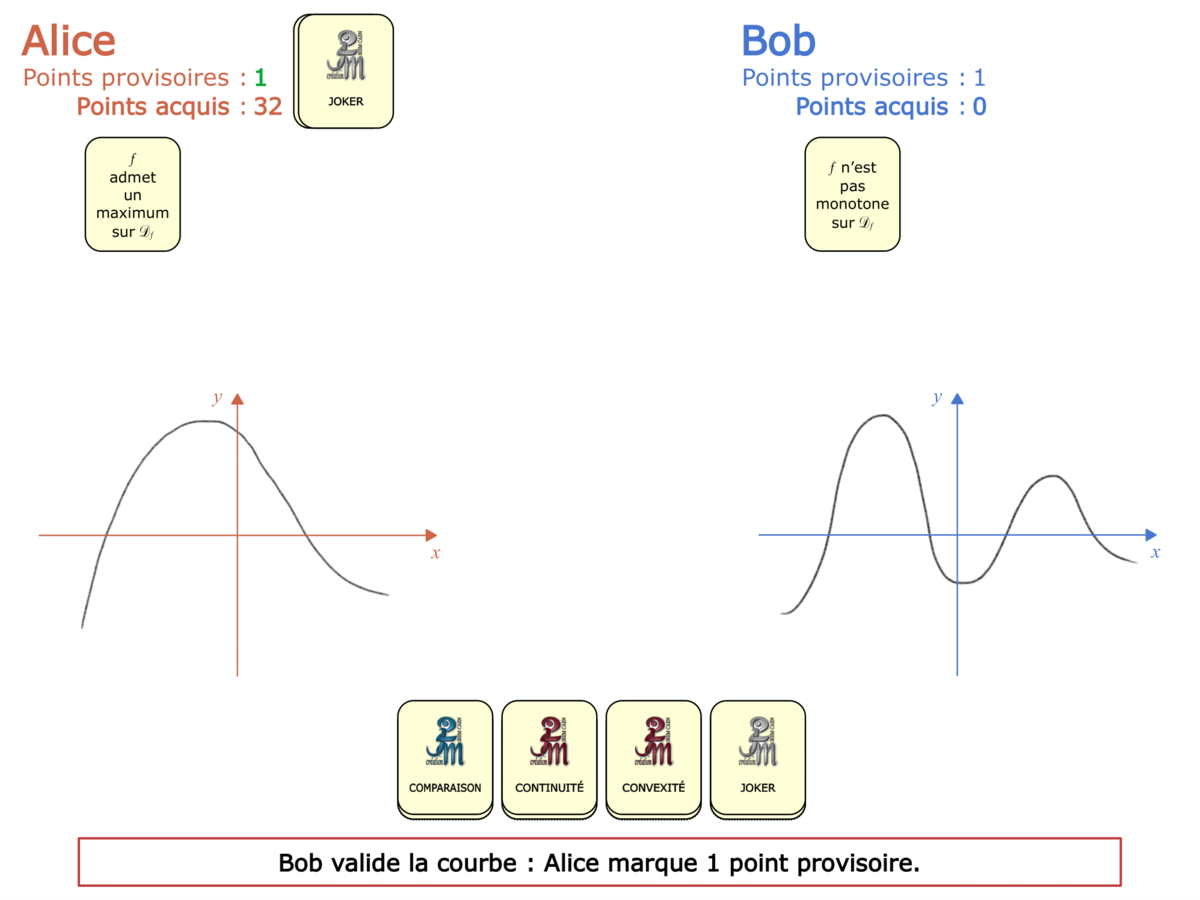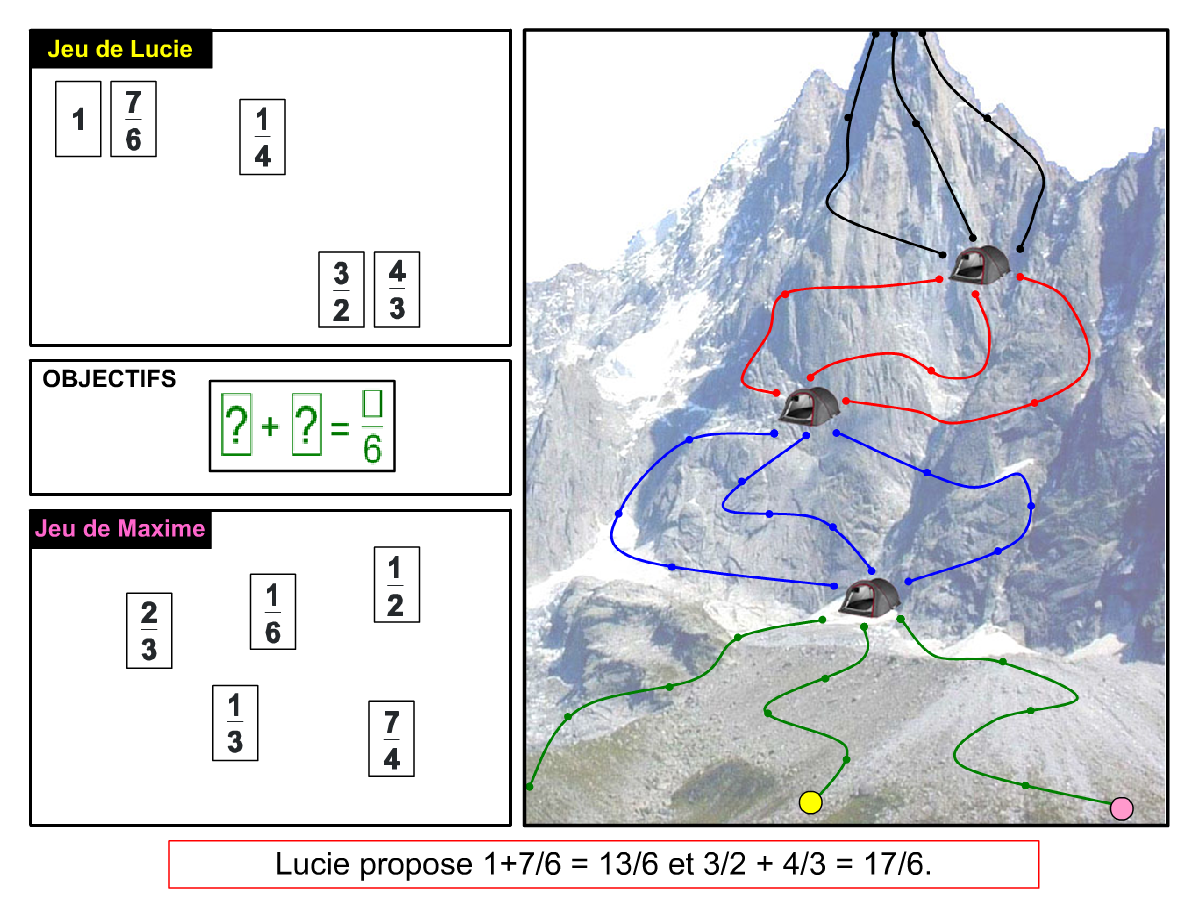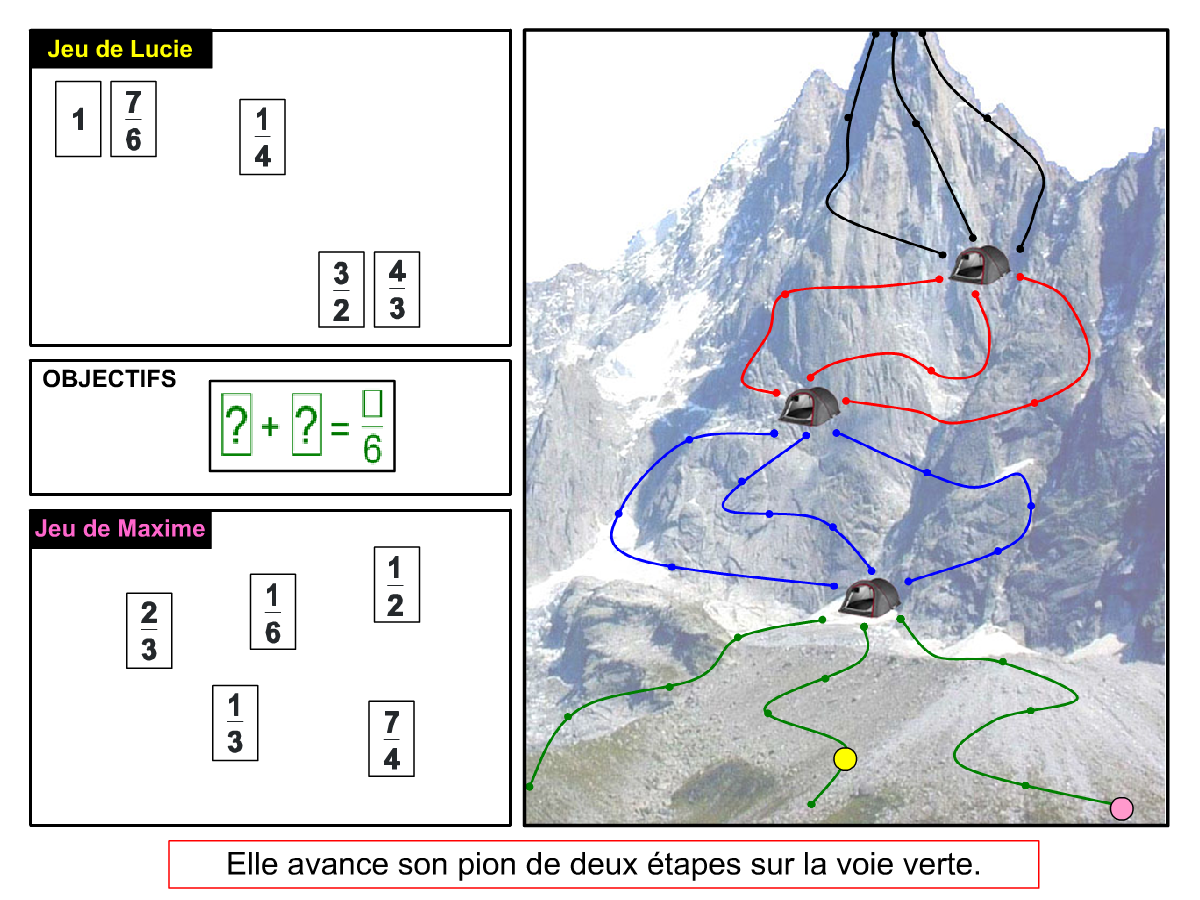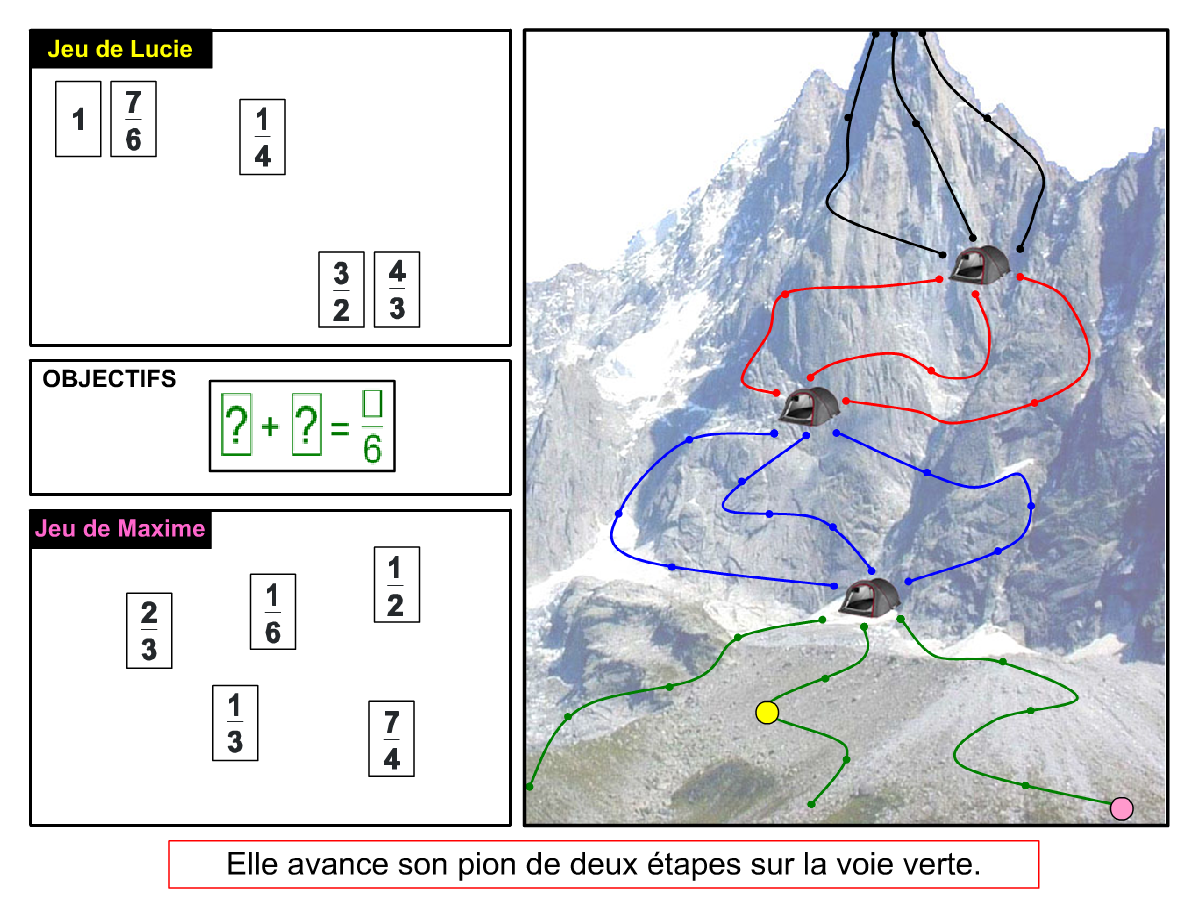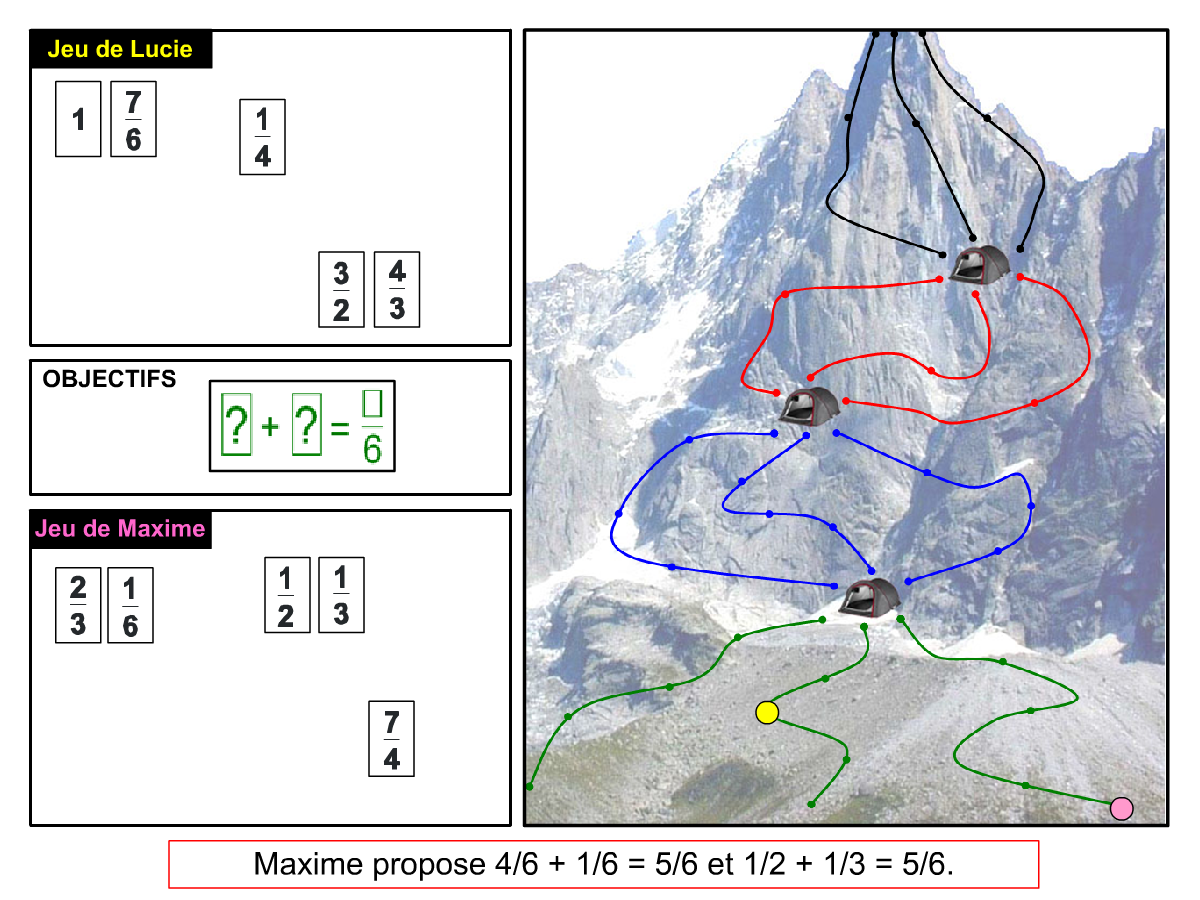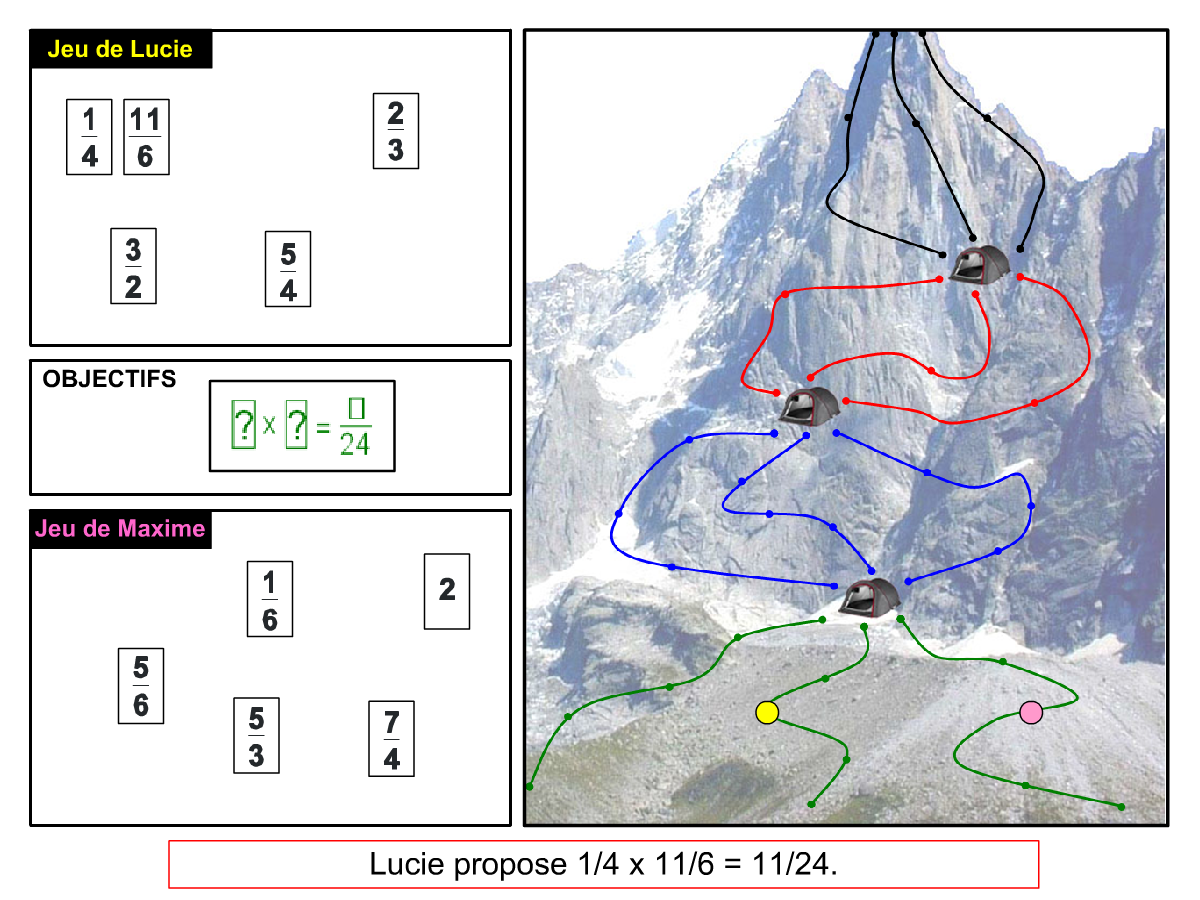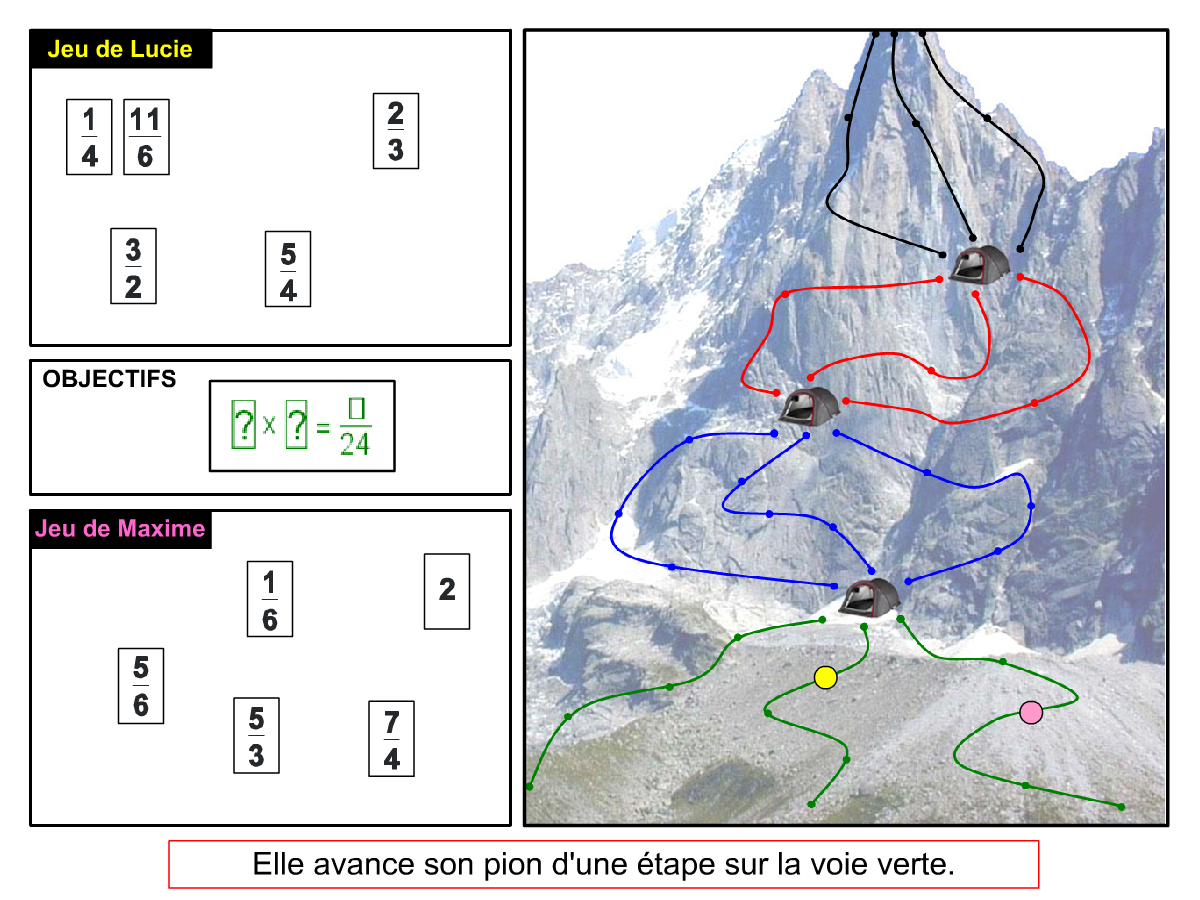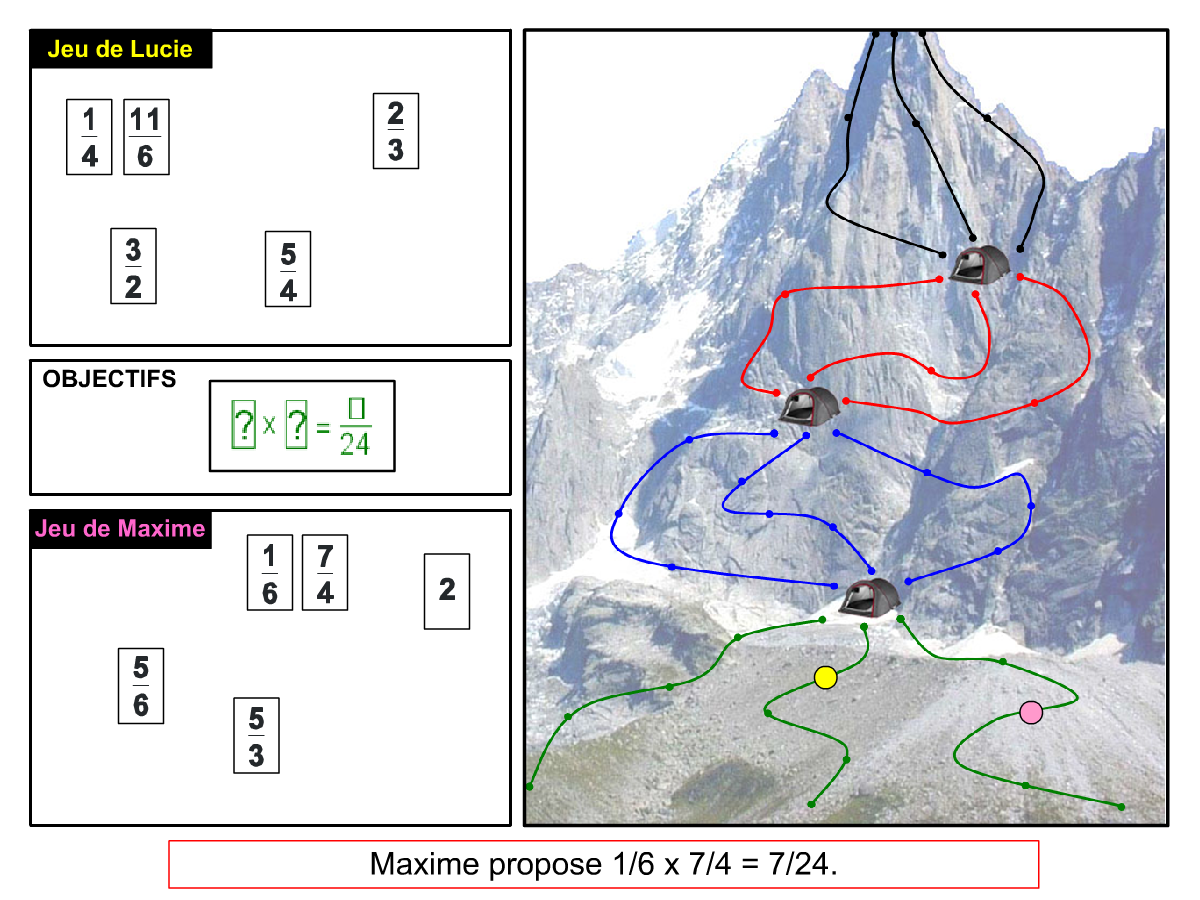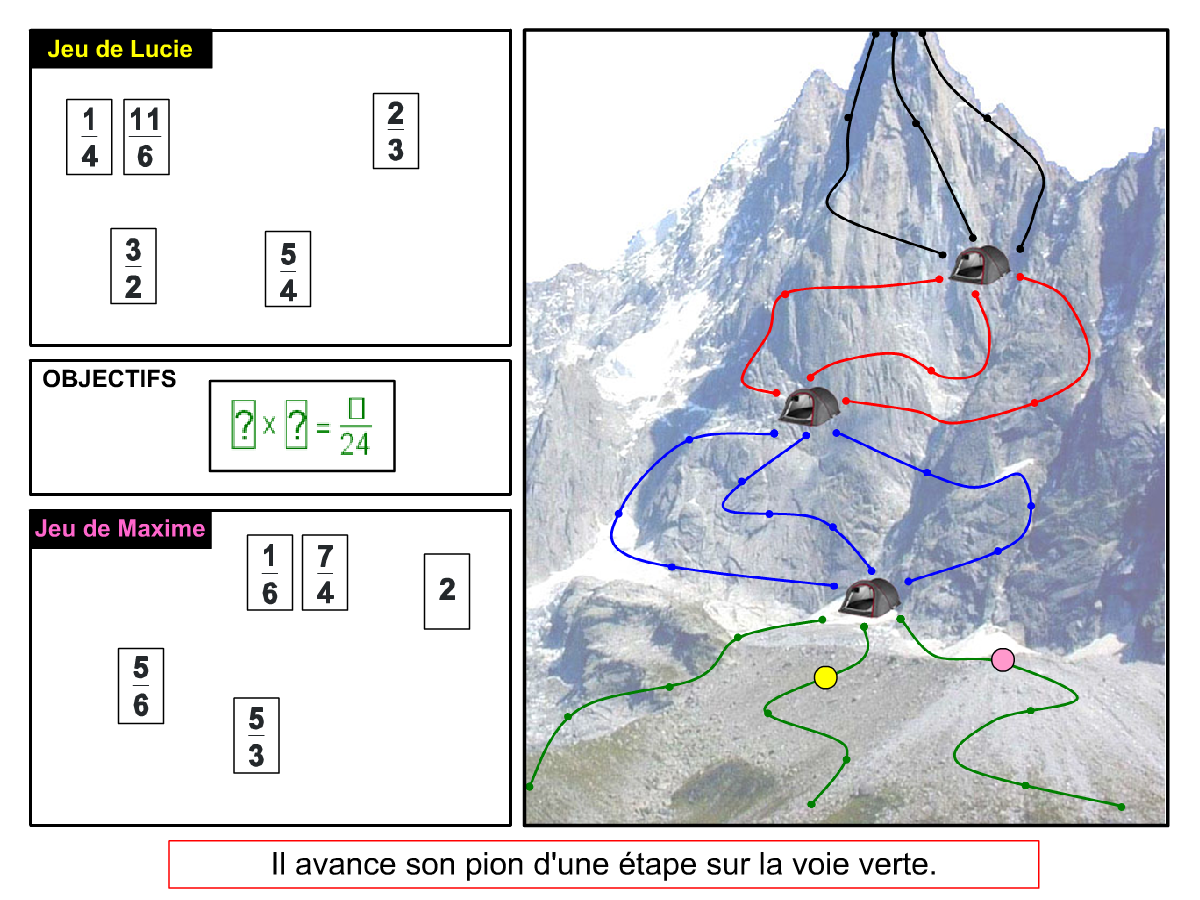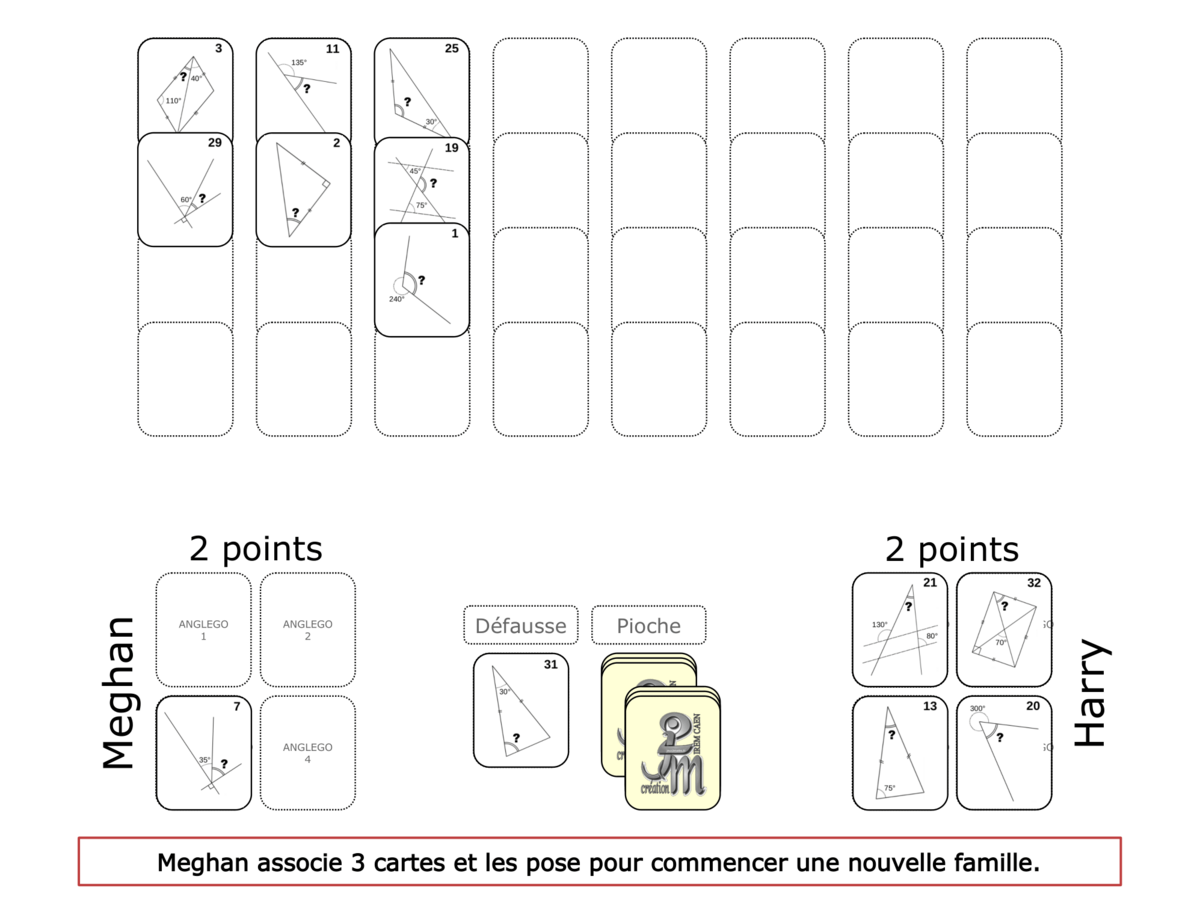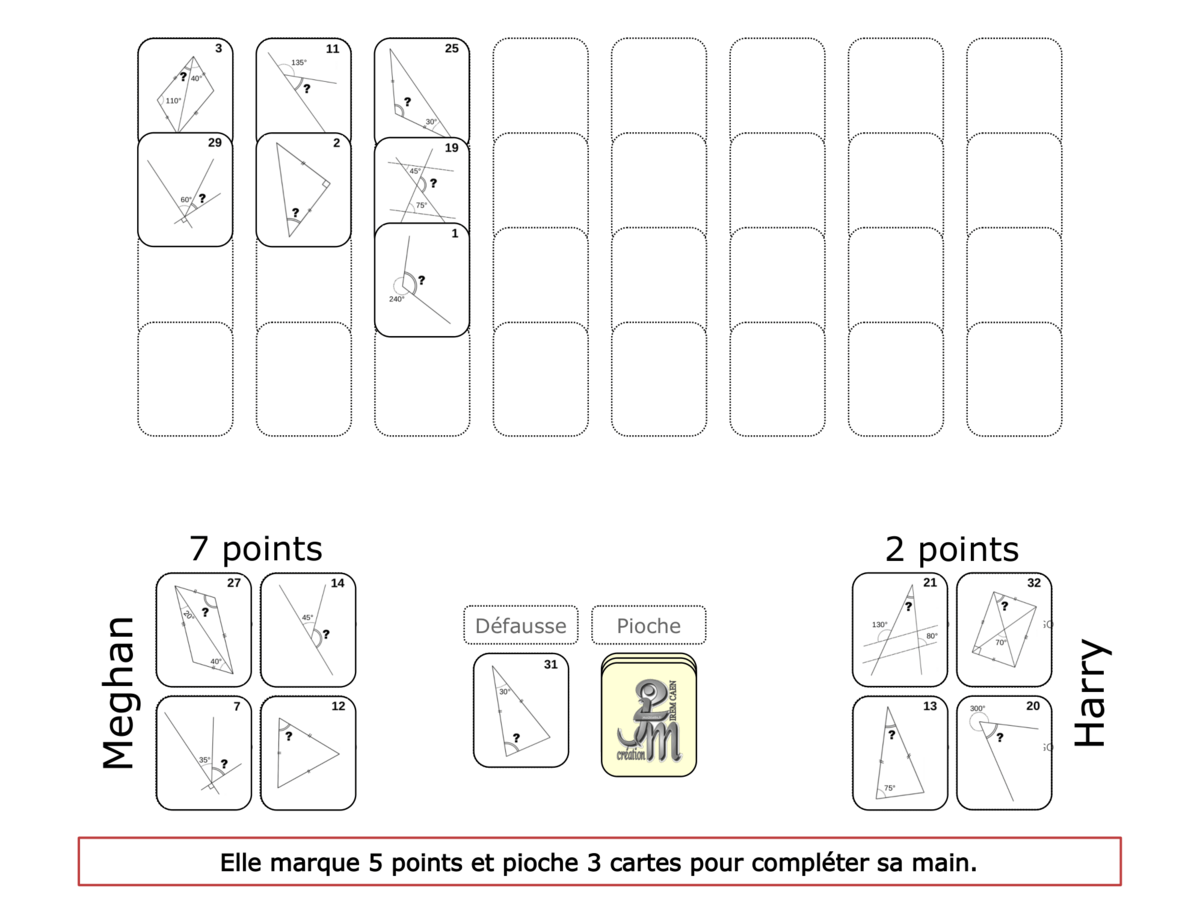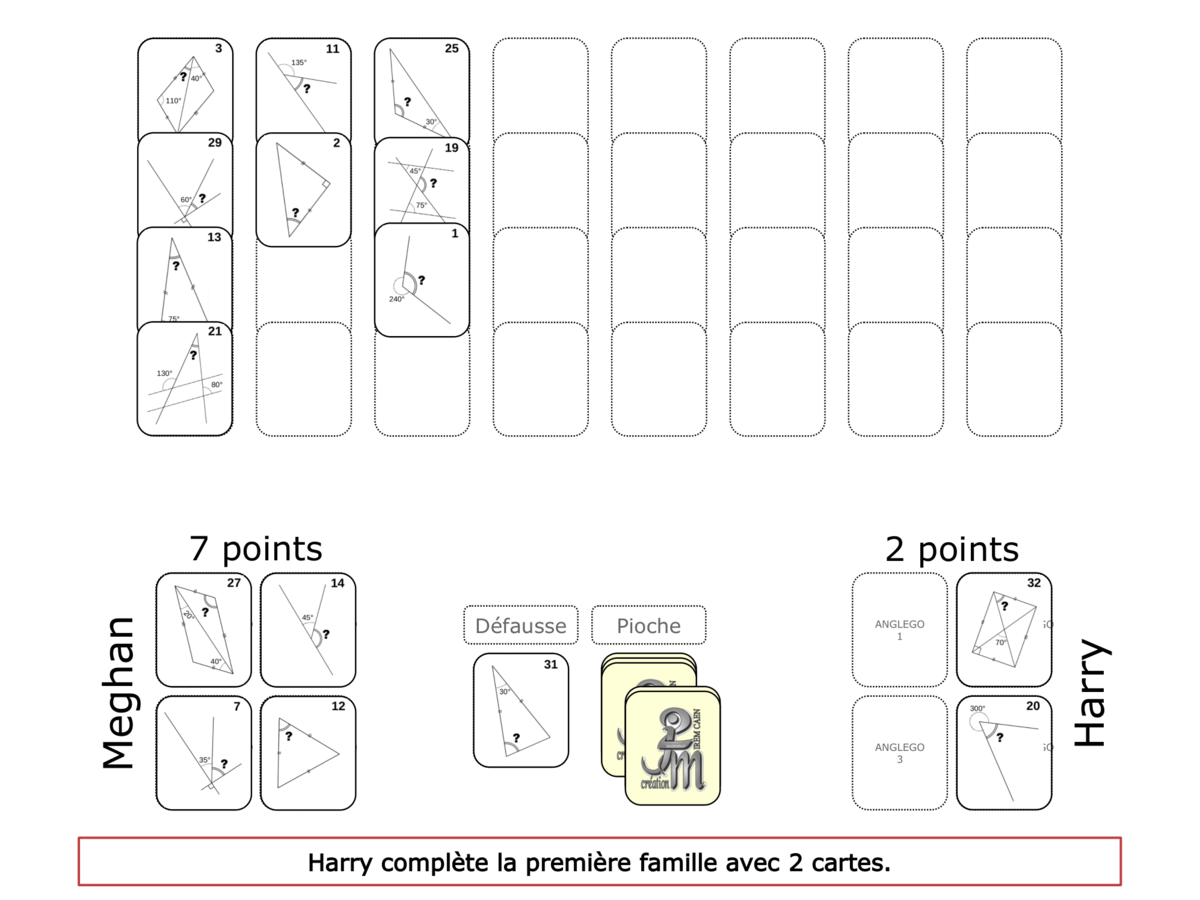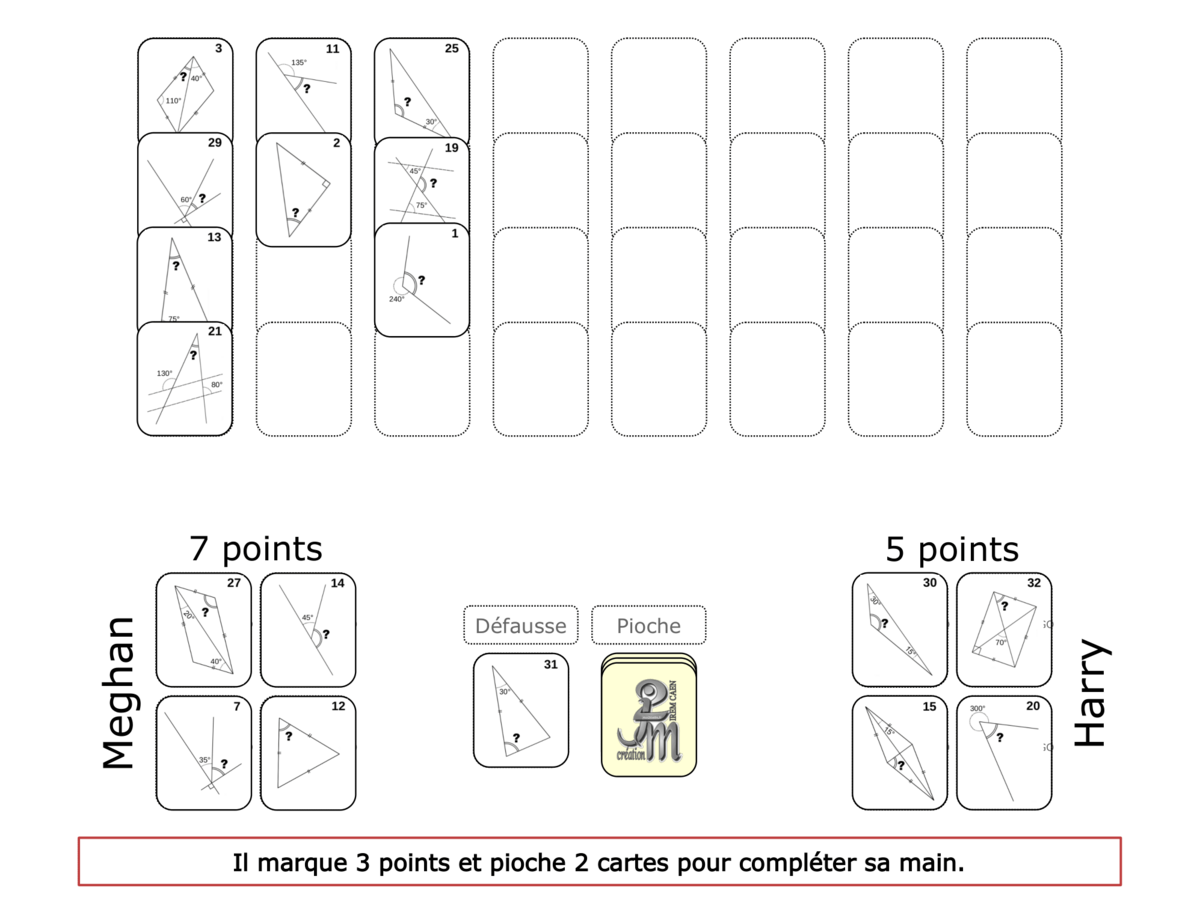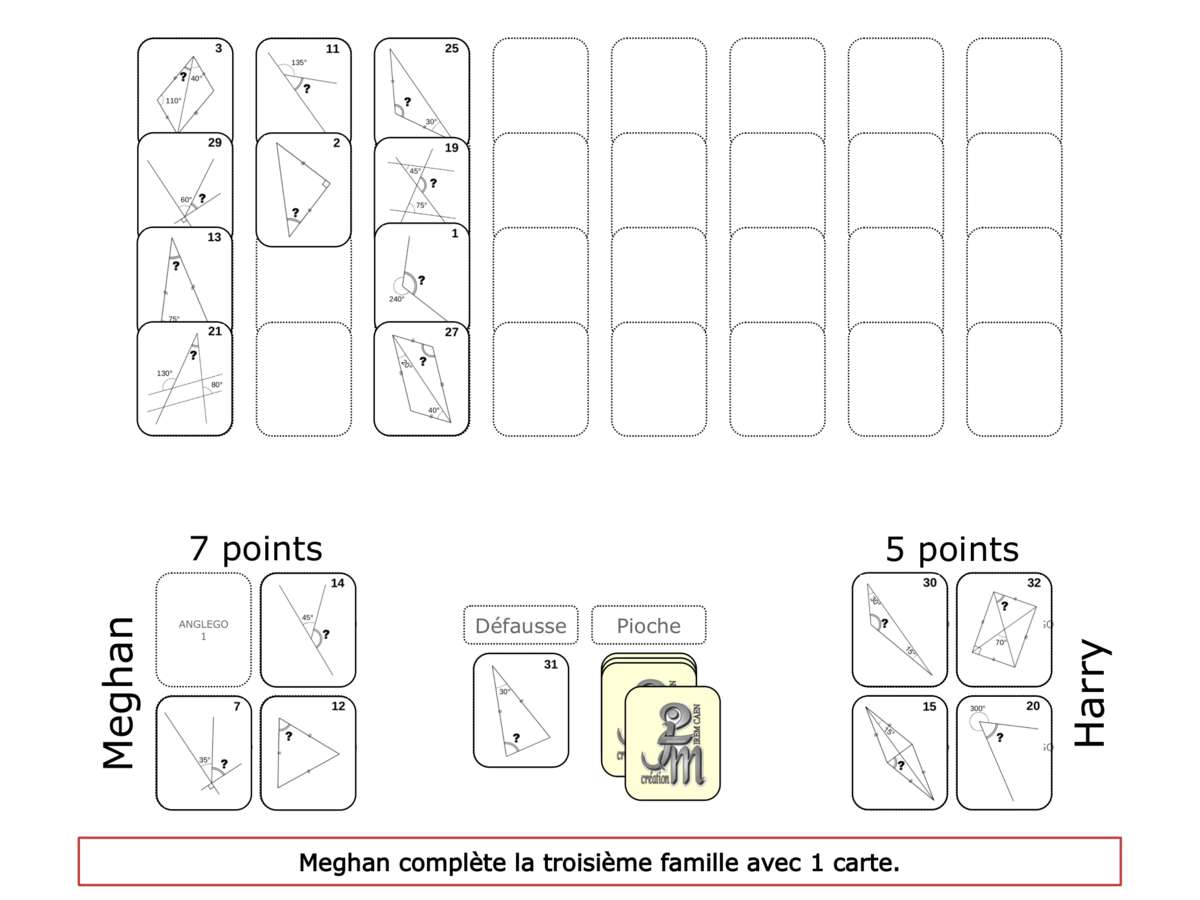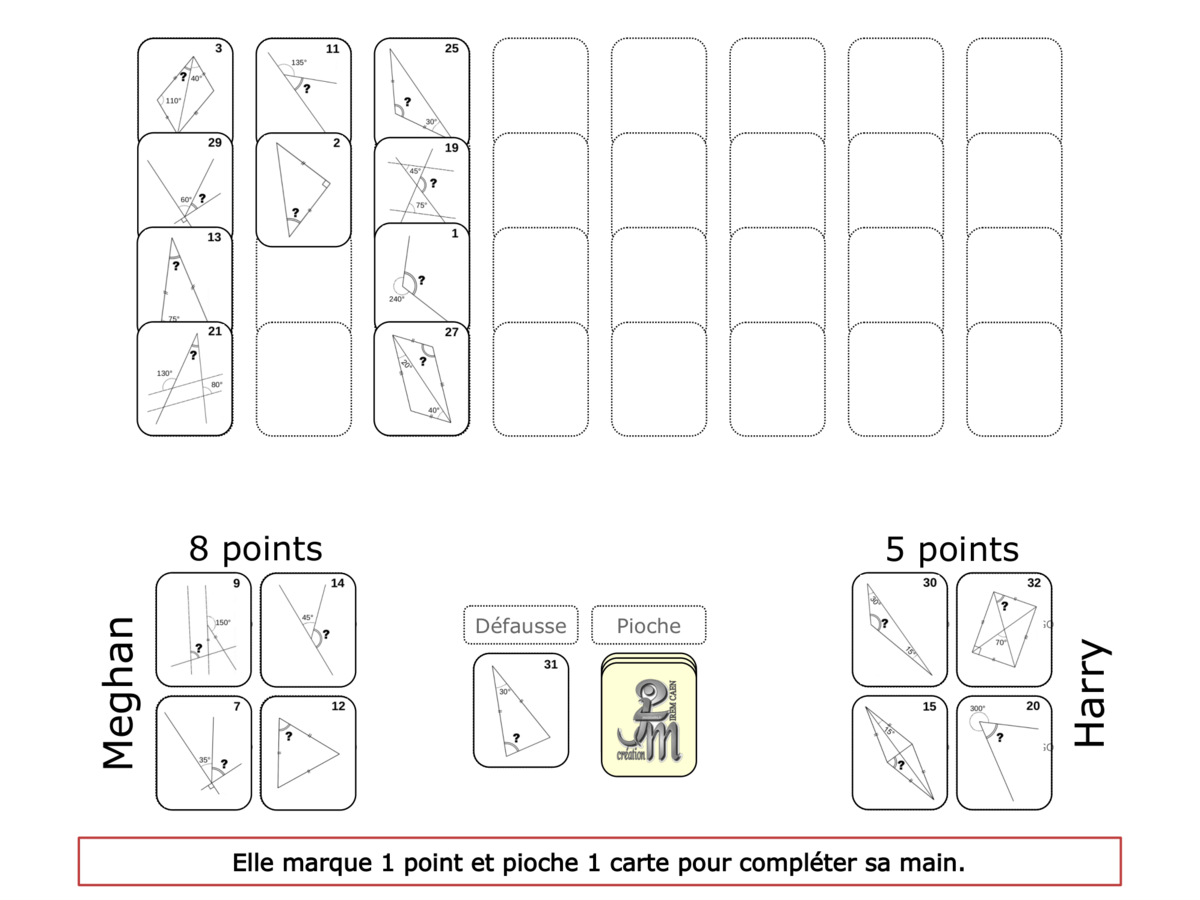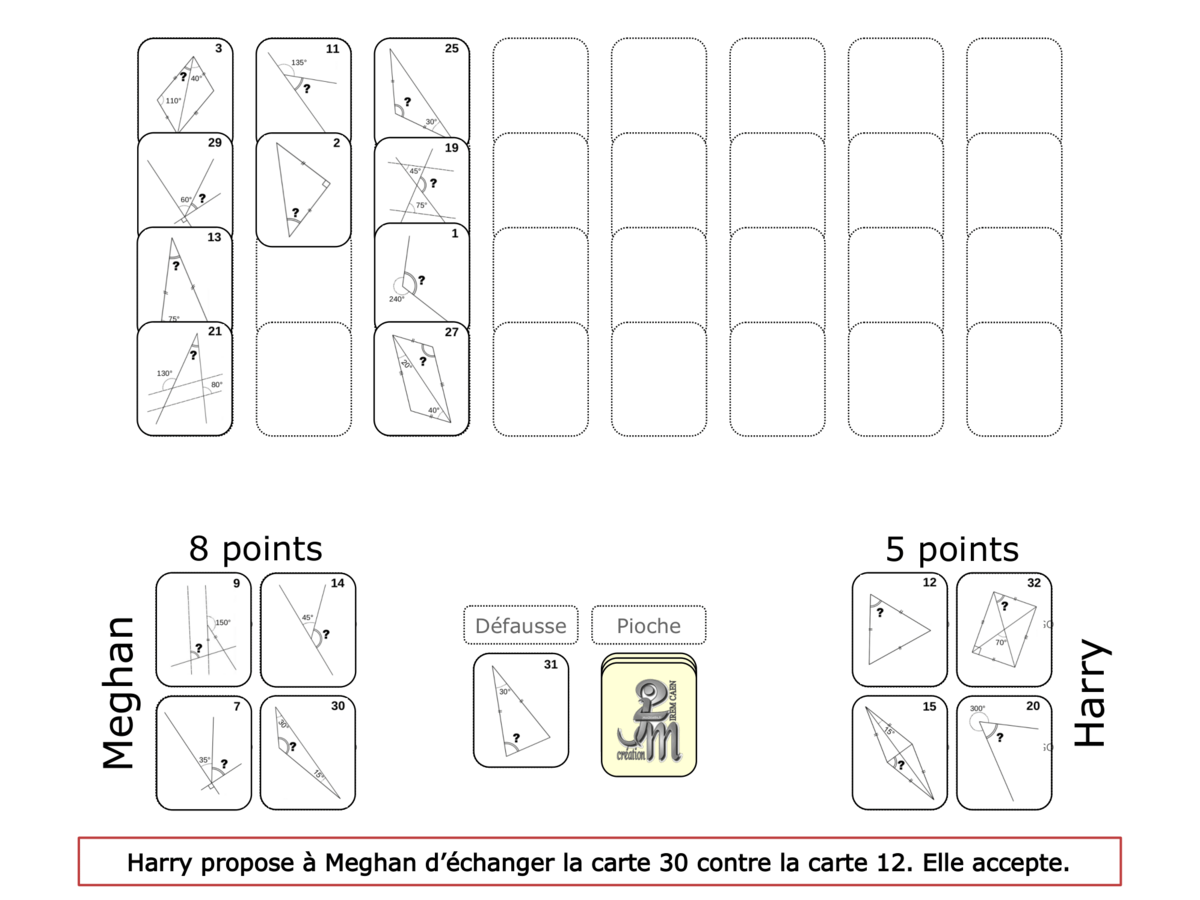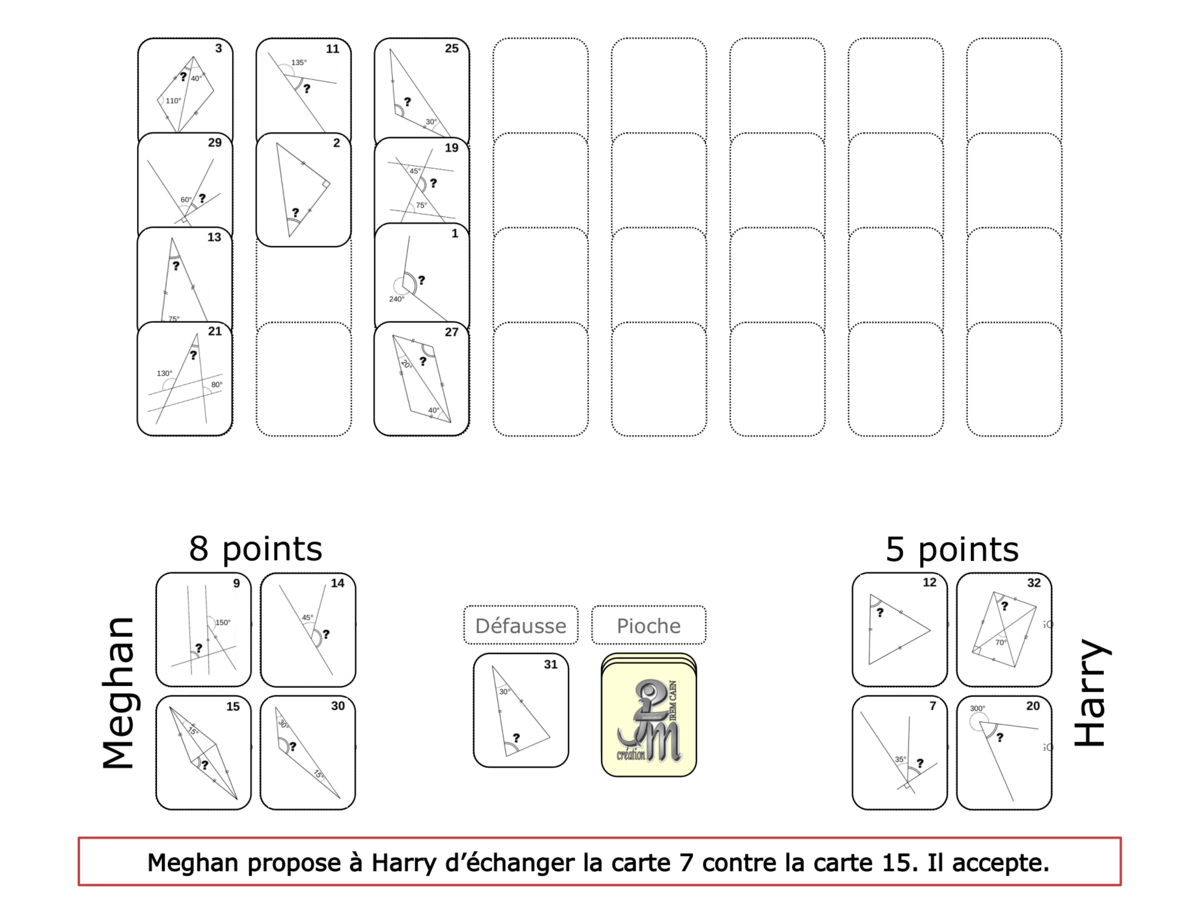

Convictions
Animateurs à l’IREM de Caen-Normandie, c’est à l’occasion d’une recherche d’activité concernant la somme des vecteurs que nous avons été amenés à créer un jeu : les «Vectominos». D’abord simple «ressort didactique» pour aborder une notion délicate de façon peu conventionnelle, il nous est apparu que nos élèves prenaient beaucoup de plaisir à y jouer et que la pratique du jeu améliorait sensiblement les performances globales. Dans le but de développer ce type d’activité, nous avons créé un nouveau groupe de recherche IREM, le groupe «Jeux2Maths».
Depuis 2001, notre travail a été de concevoir des jeux abordant différentes notions des programmes du collège et de les tester dans nos classes pour juger leur pertinence et leur impact sur les élèves. Si nous n’avons pas encore créé d’outils évaluant l’influence du jeu sur l’apprentissage, nous avons toujours constaté dans nos pratiques que la réaction des élèves était toujours très positive, qu’ils prenaient un plaisir évident à faire des maths, et que les situations de jeu influaient nettement sur leur implication et leur désir de réussite.
Les ateliers que nous avons animés lors des journées régionales de l’APMEP de Basse-Normandie et des journées nationales de l’APMEP de Rennes (2002) et de Caen (2005), notre participation aux groupes de travail et d’échange auprès des PLC2 de l’IUFM de Caen (depuis 2003) ainsi que les stages proposés au Plan Académique de Formation (depuis 2004) qui ont fait l’objet de beaucoup de candidatures, nous confortent dans l’idée que la pratique du jeu en classe suscite l’intérêt et la curiosité des collègues et nous engagent à donner plus d’écho à notre travail.
Vous ne trouverez aucun des jeux présentés dans ce site à la vente (à l’exception des Vectominos disponibles auprès de l’IREM de Caen). Il vous faudra mettre «la main à la pâte» avant de les proposer dans vos classes. Alors courage… à vos imprimantes, pots de colle, massicots, plastifieuses et autres feuilles cartonnées, le jeu en vaut la chandelle !
LES DOCUMENTS
Ils vous permettront d’obtenir toute information utile à la compréhension du jeu et à son utilisation en classe.
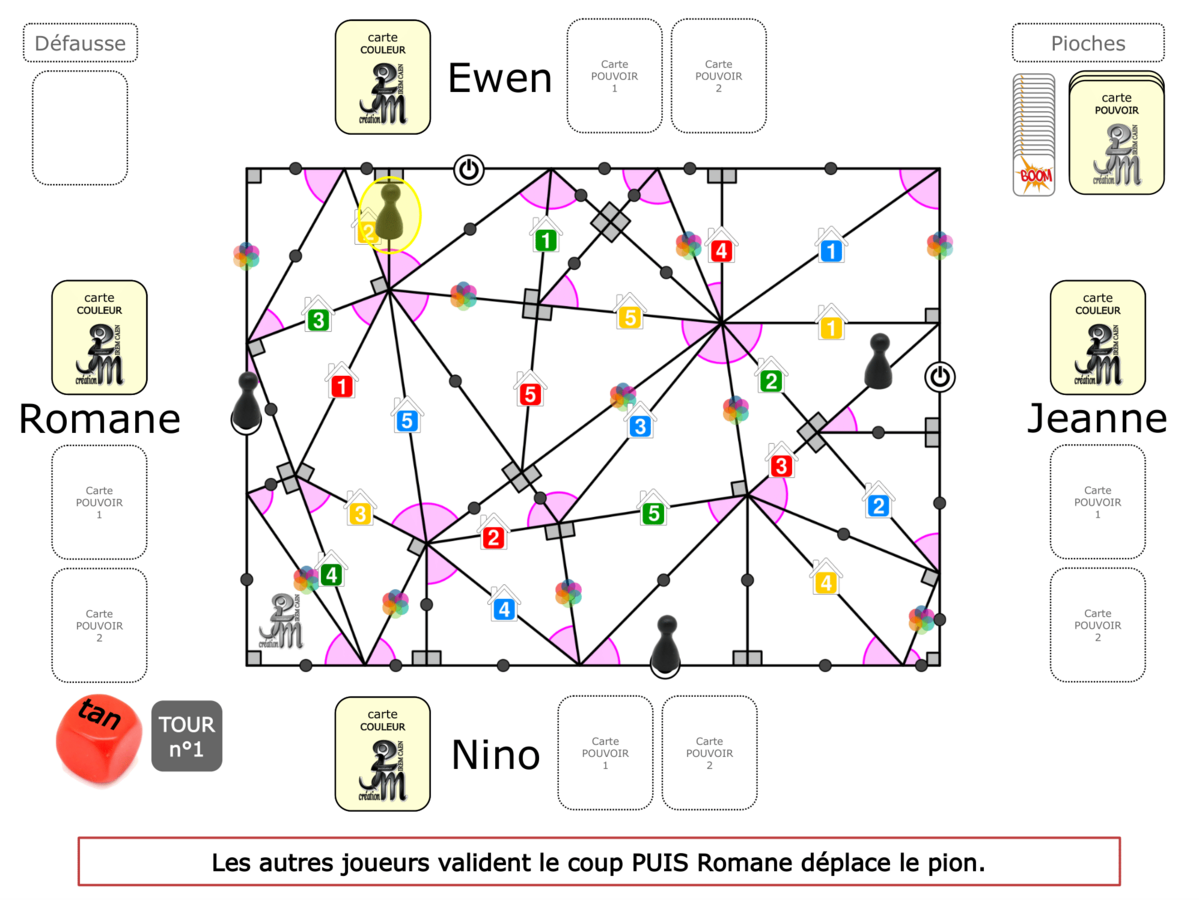
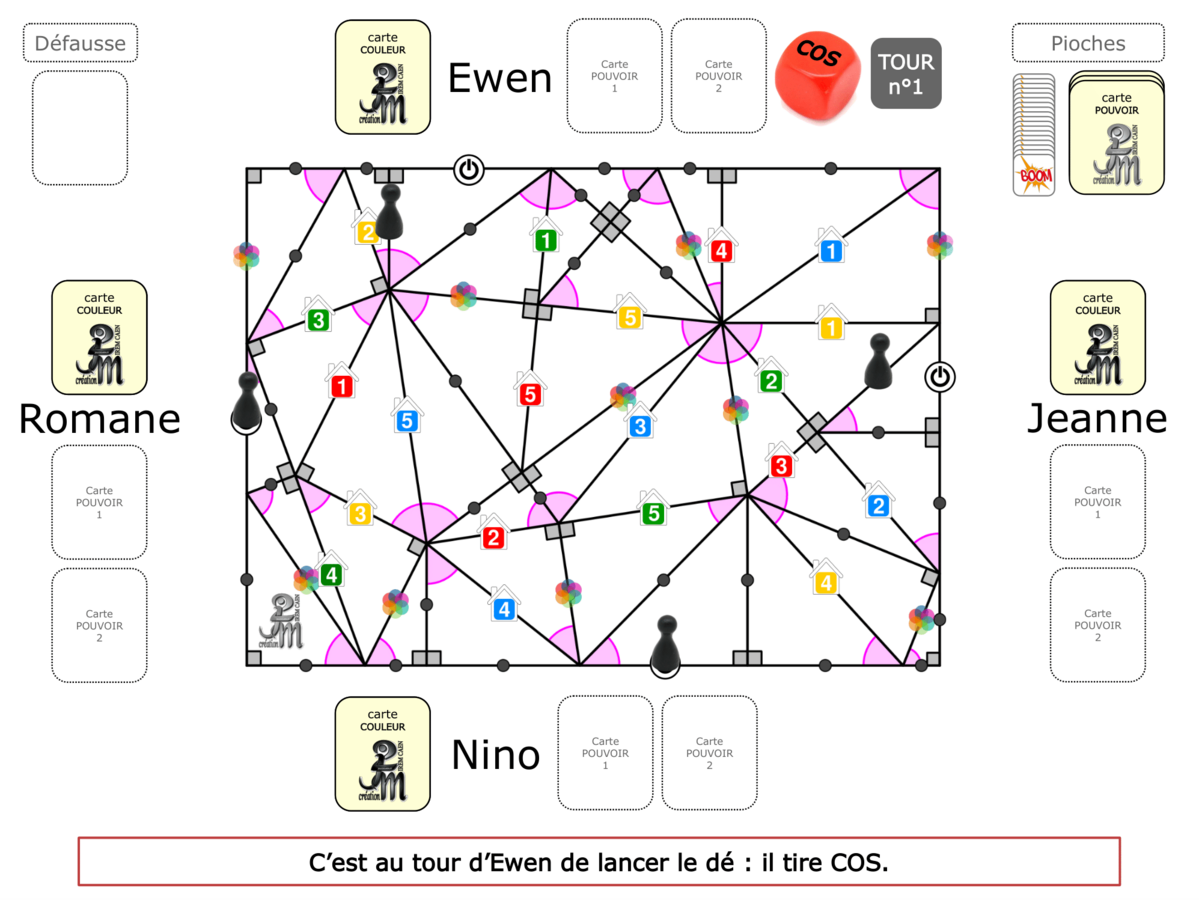
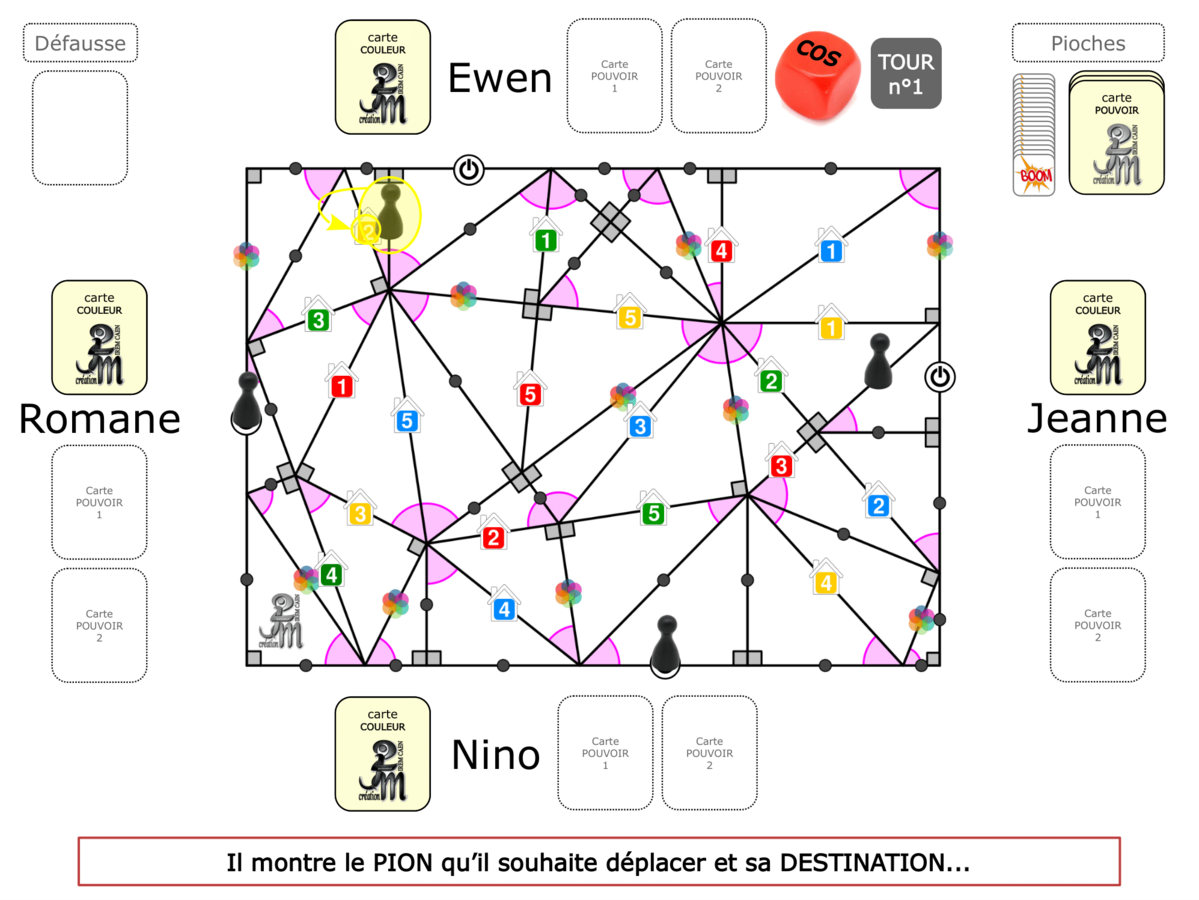
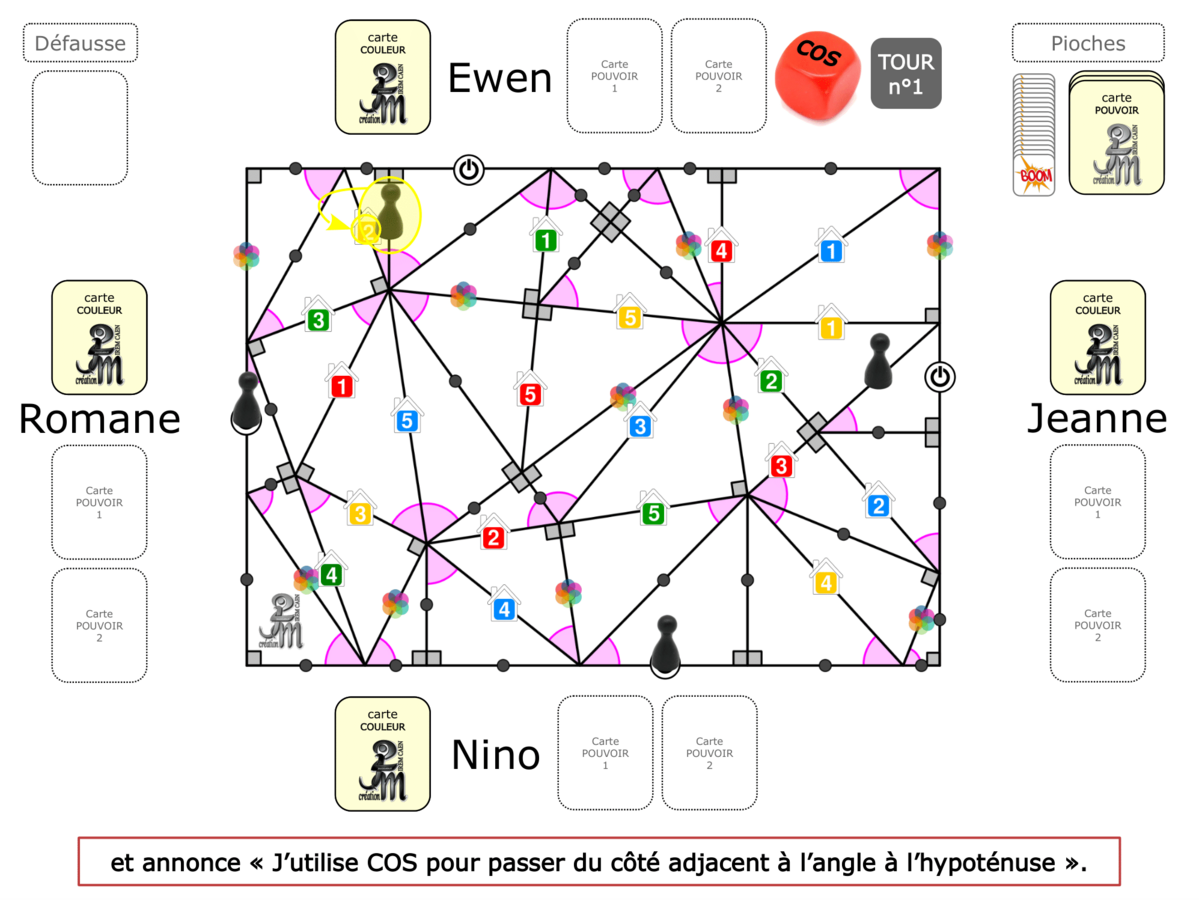
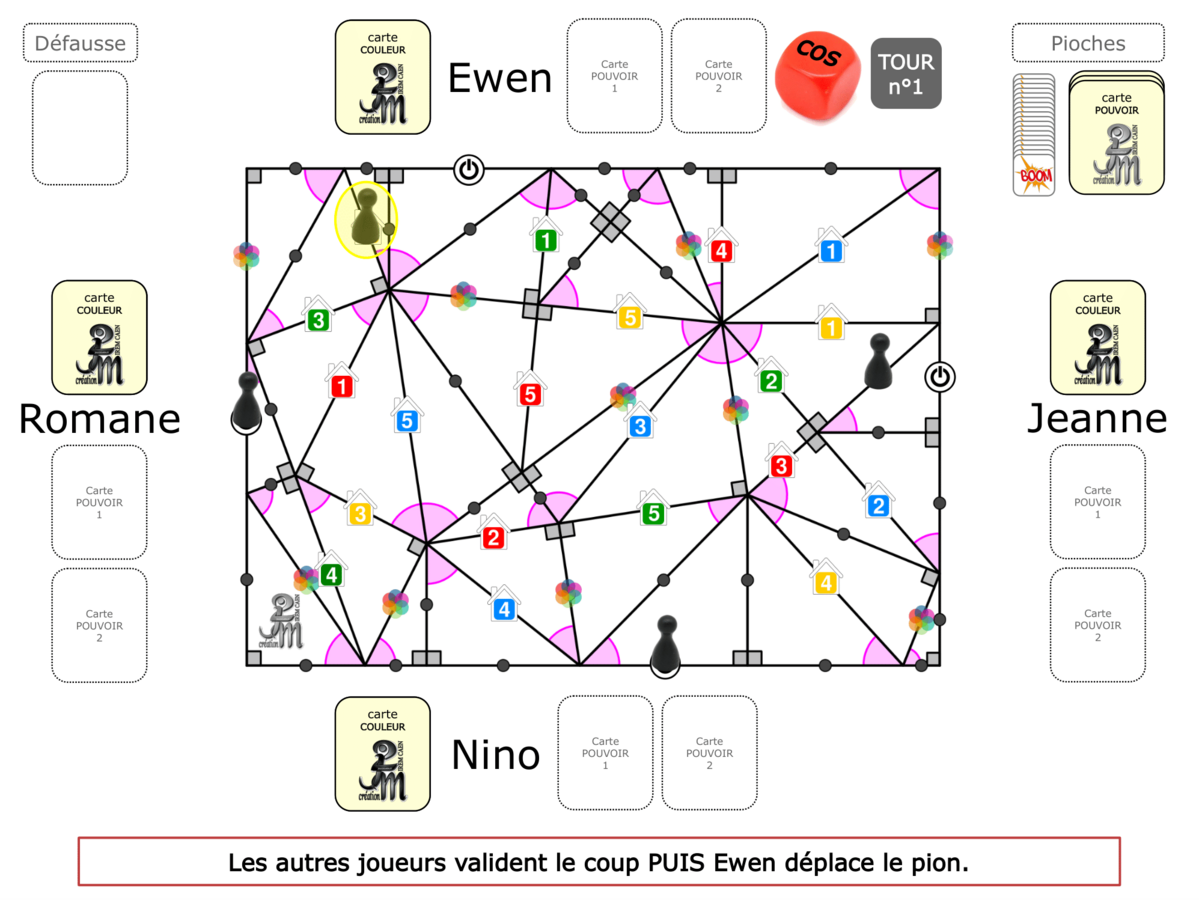
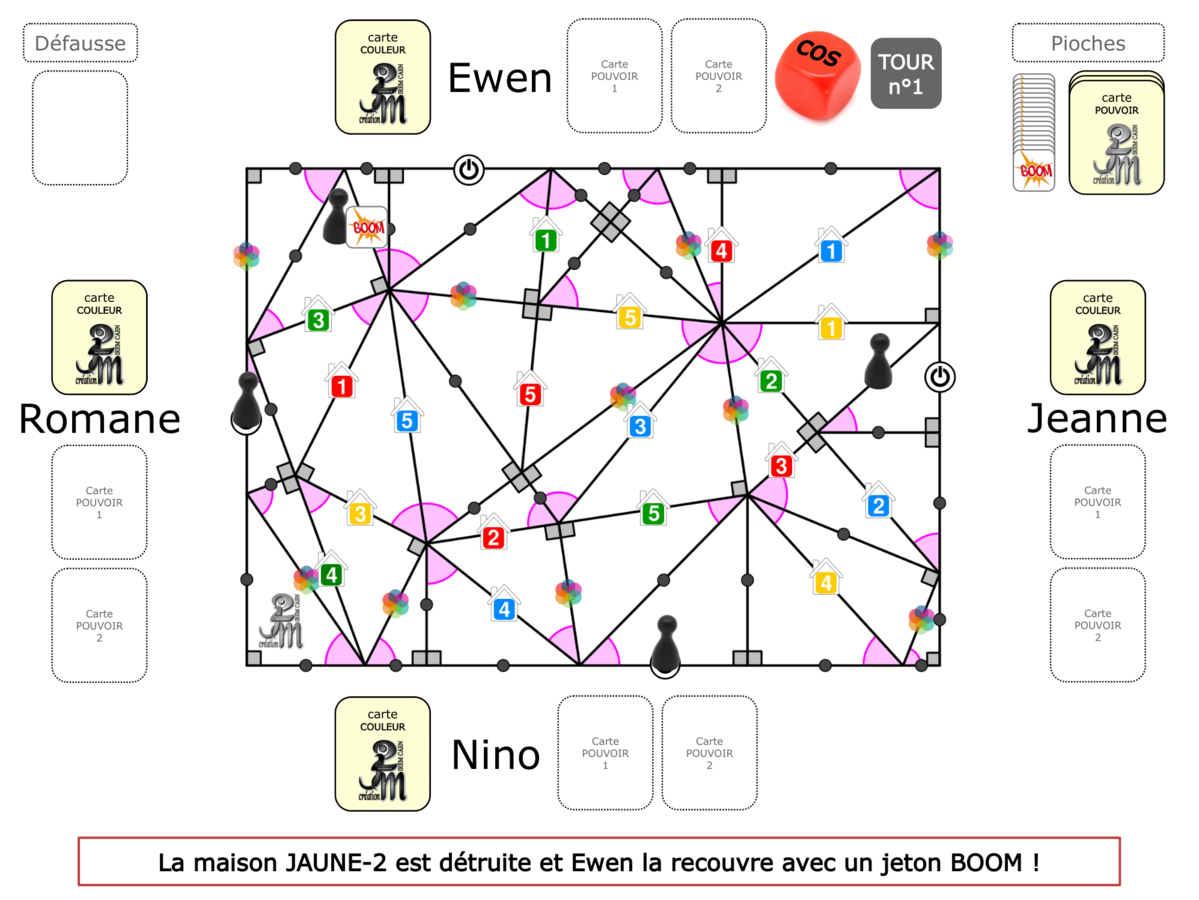
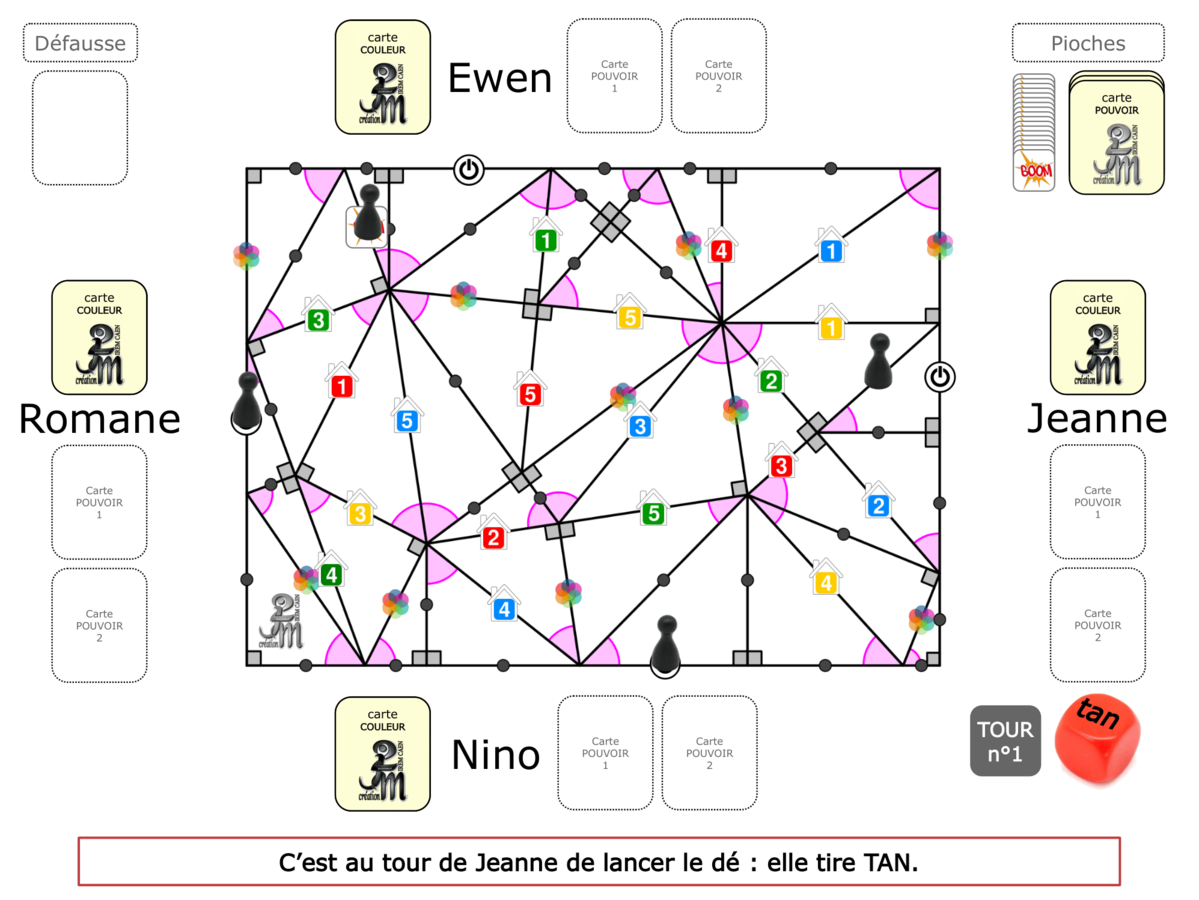
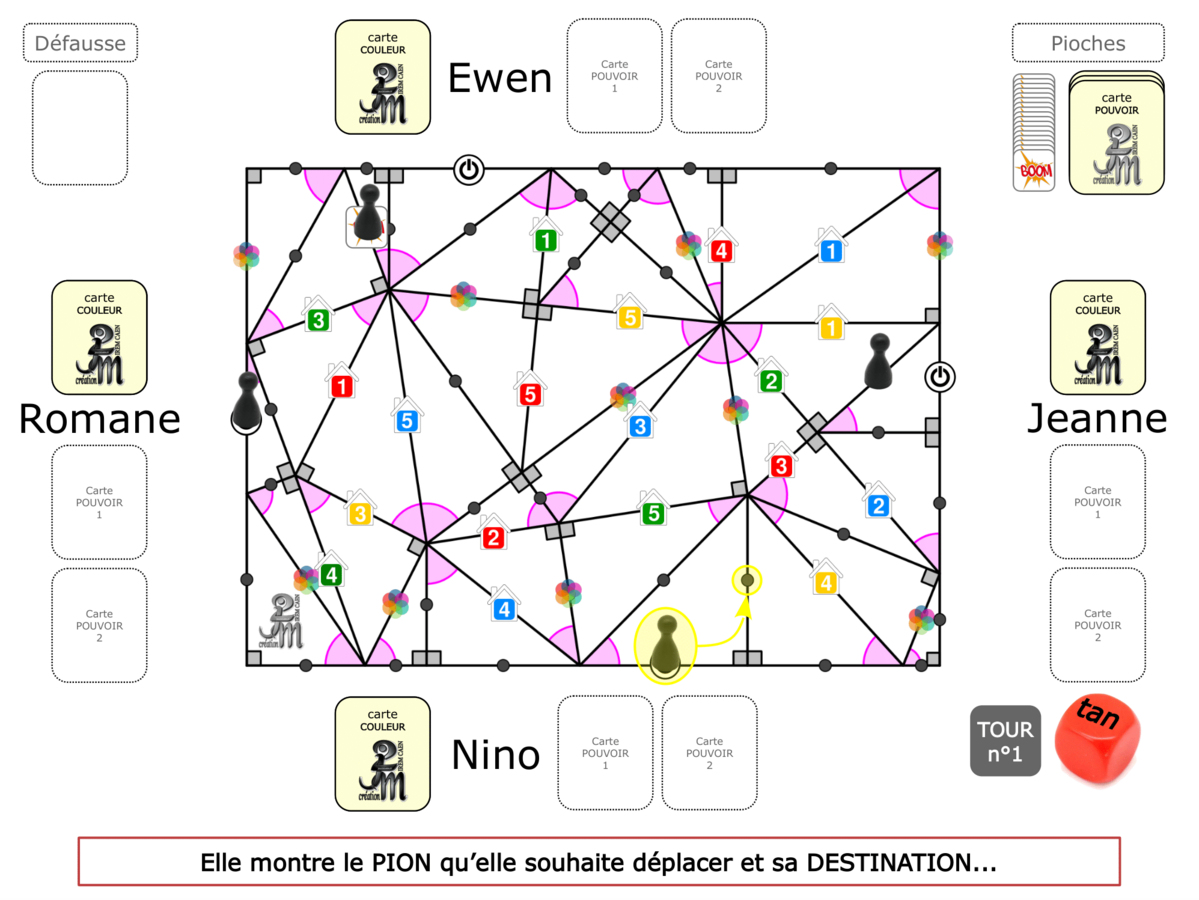
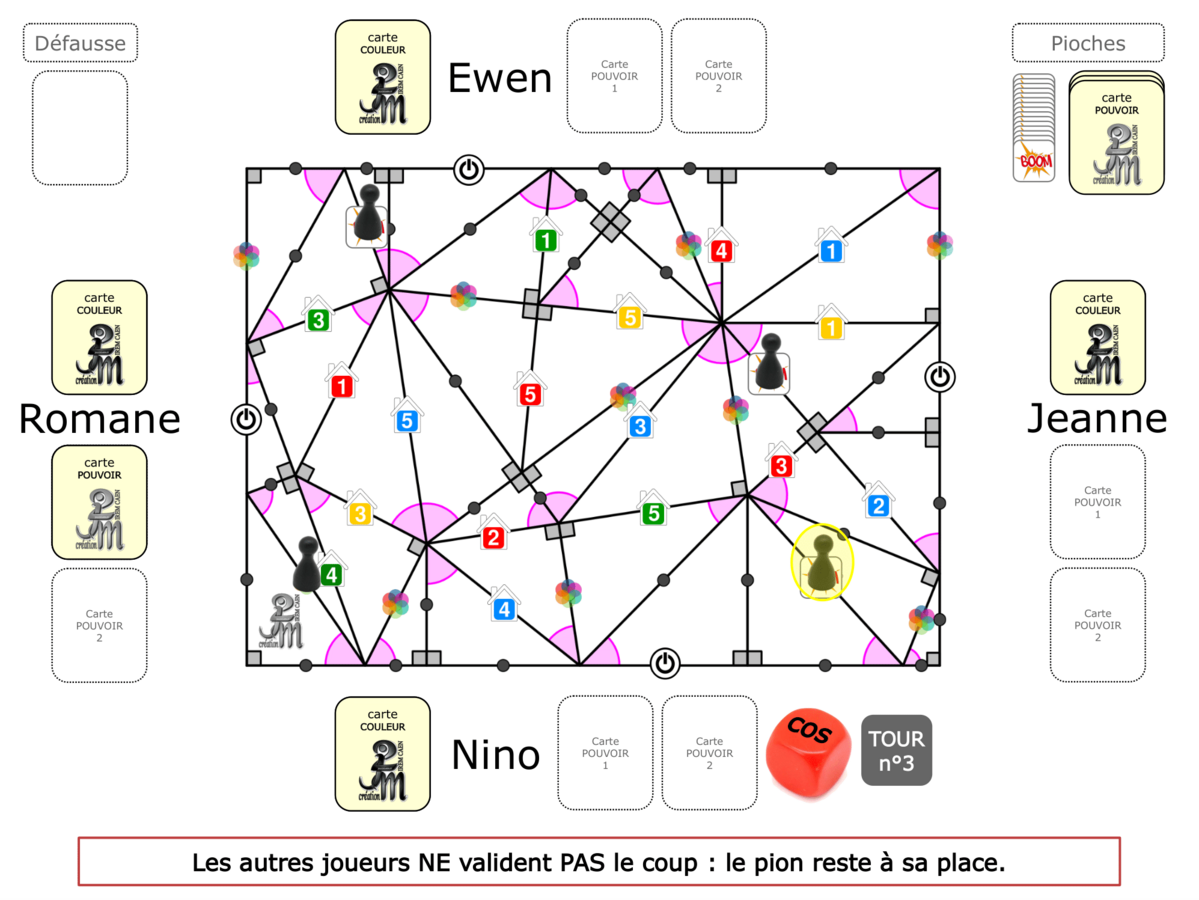
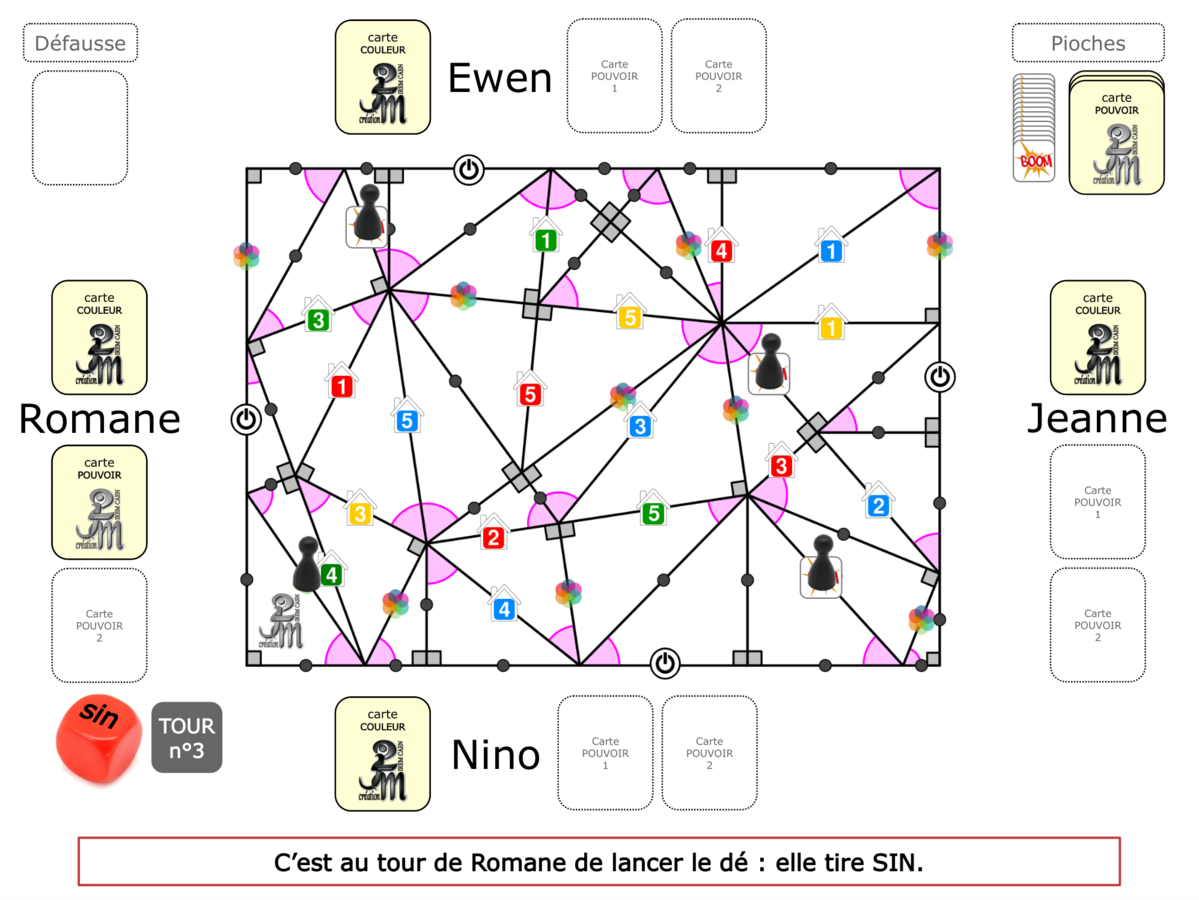
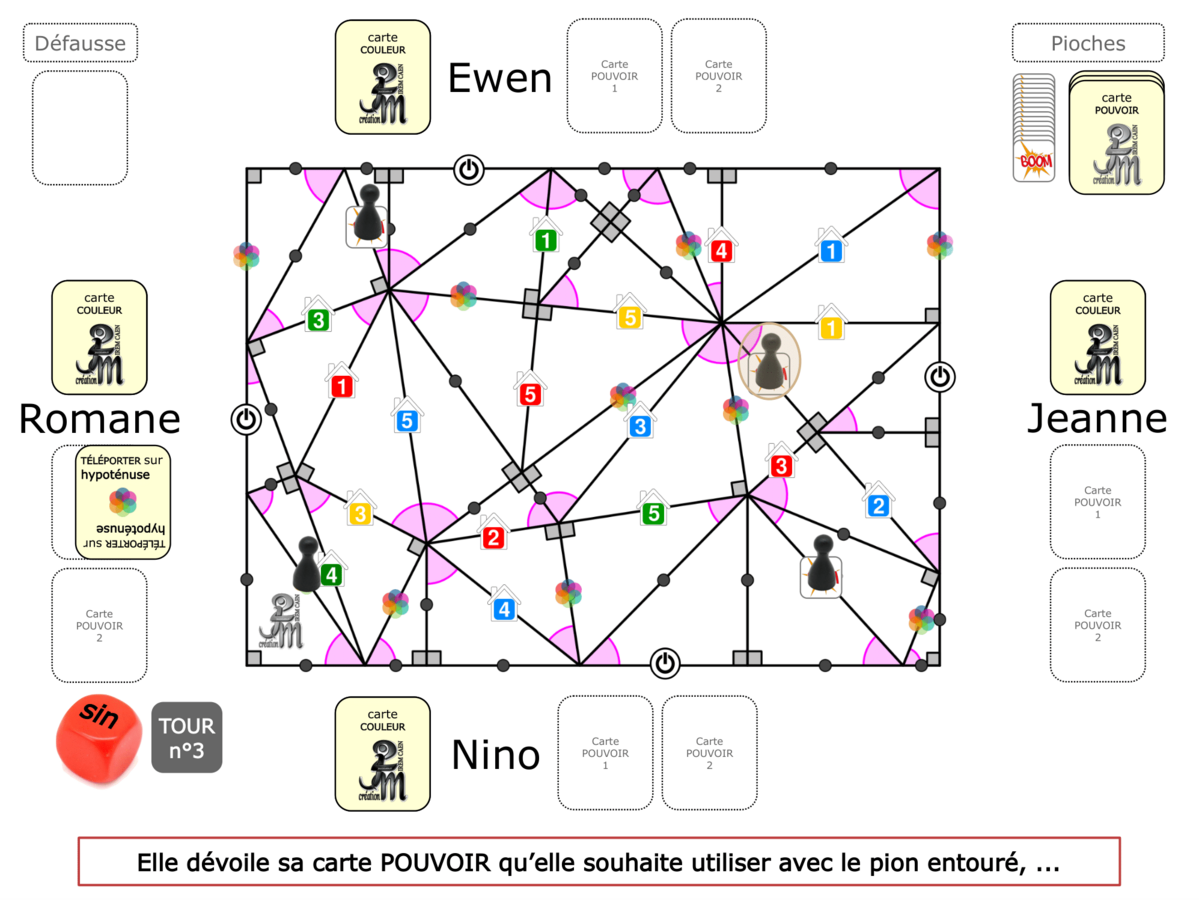
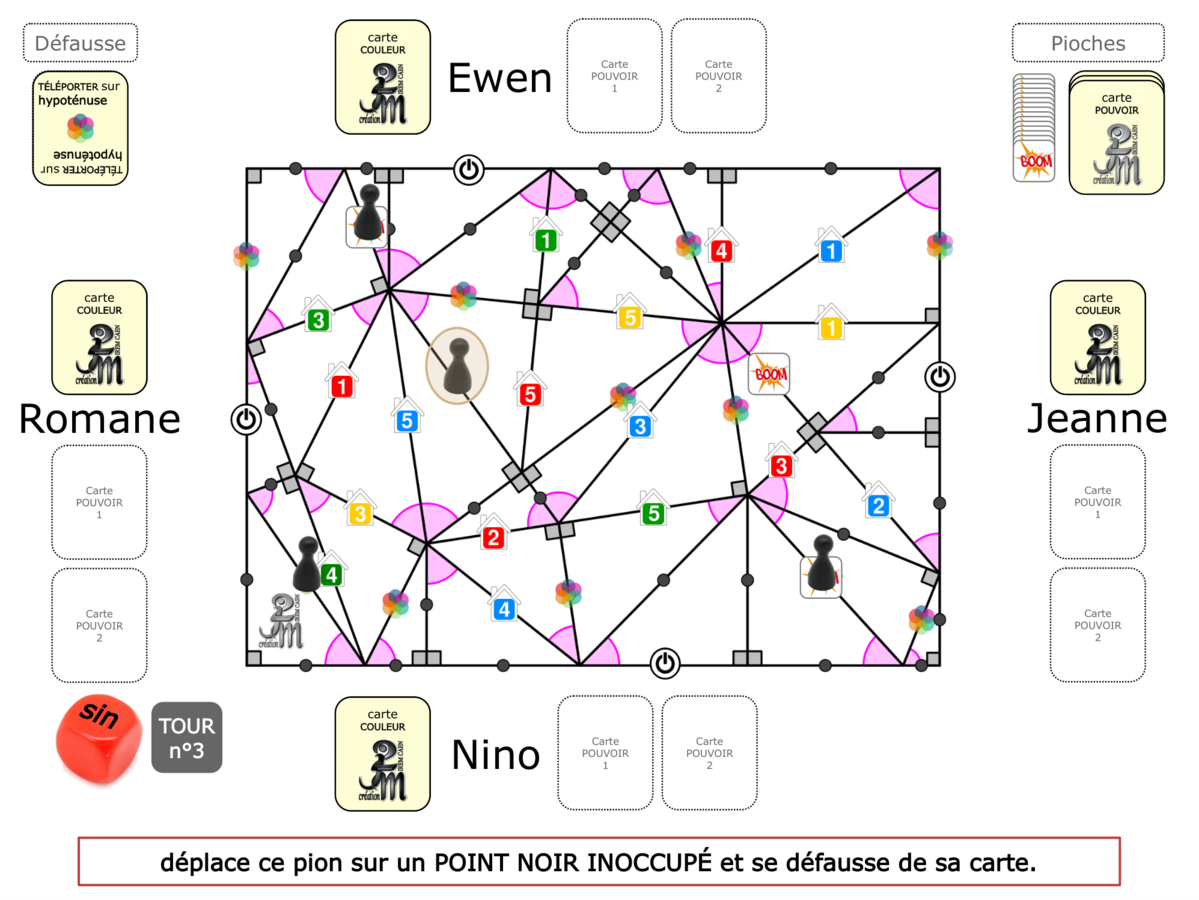
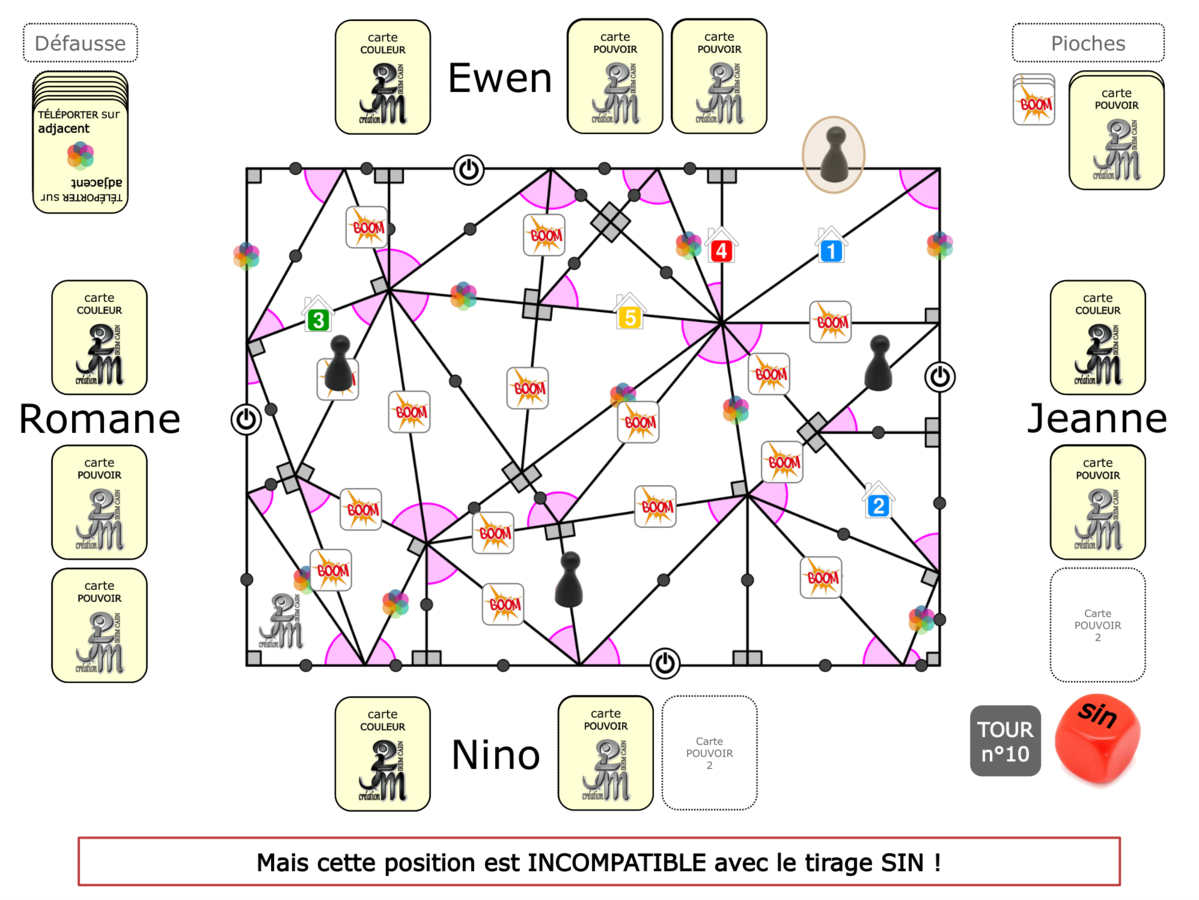
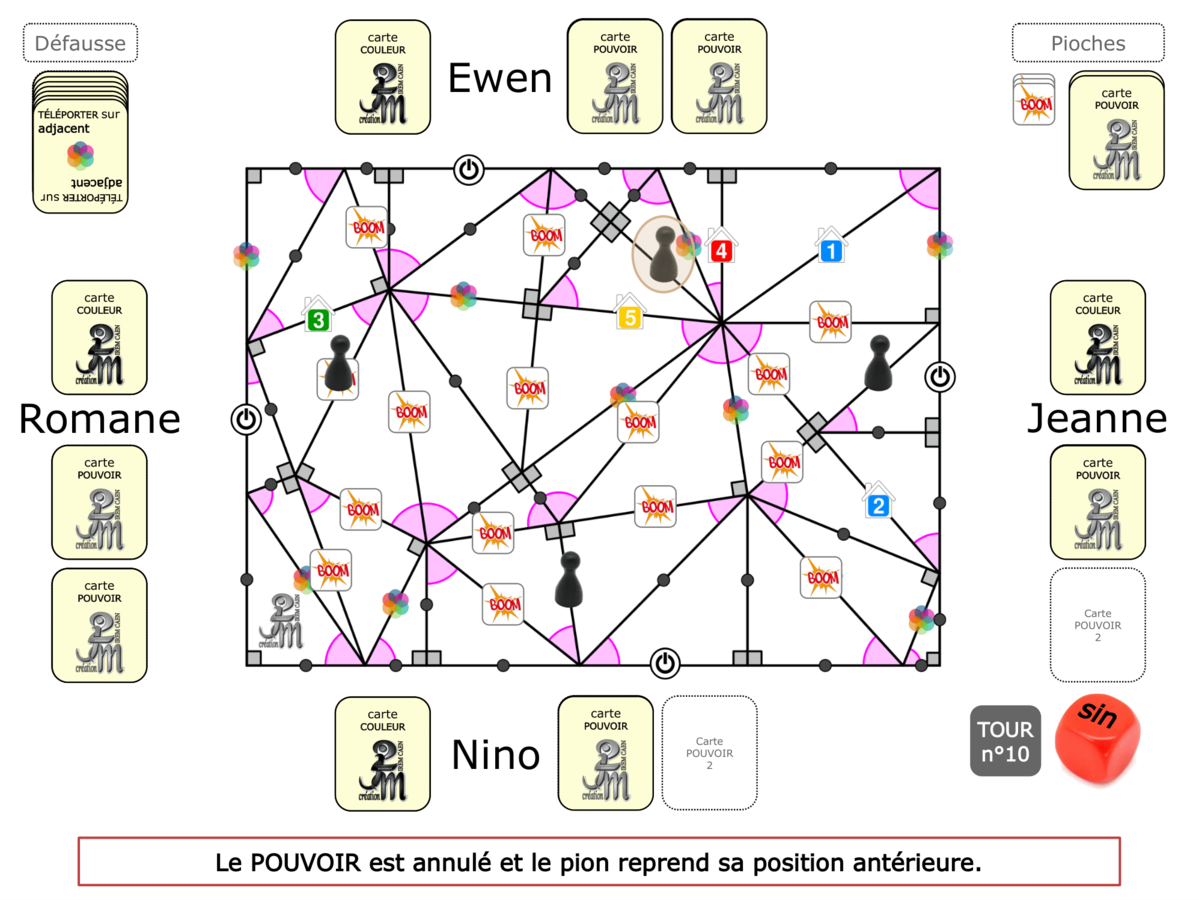
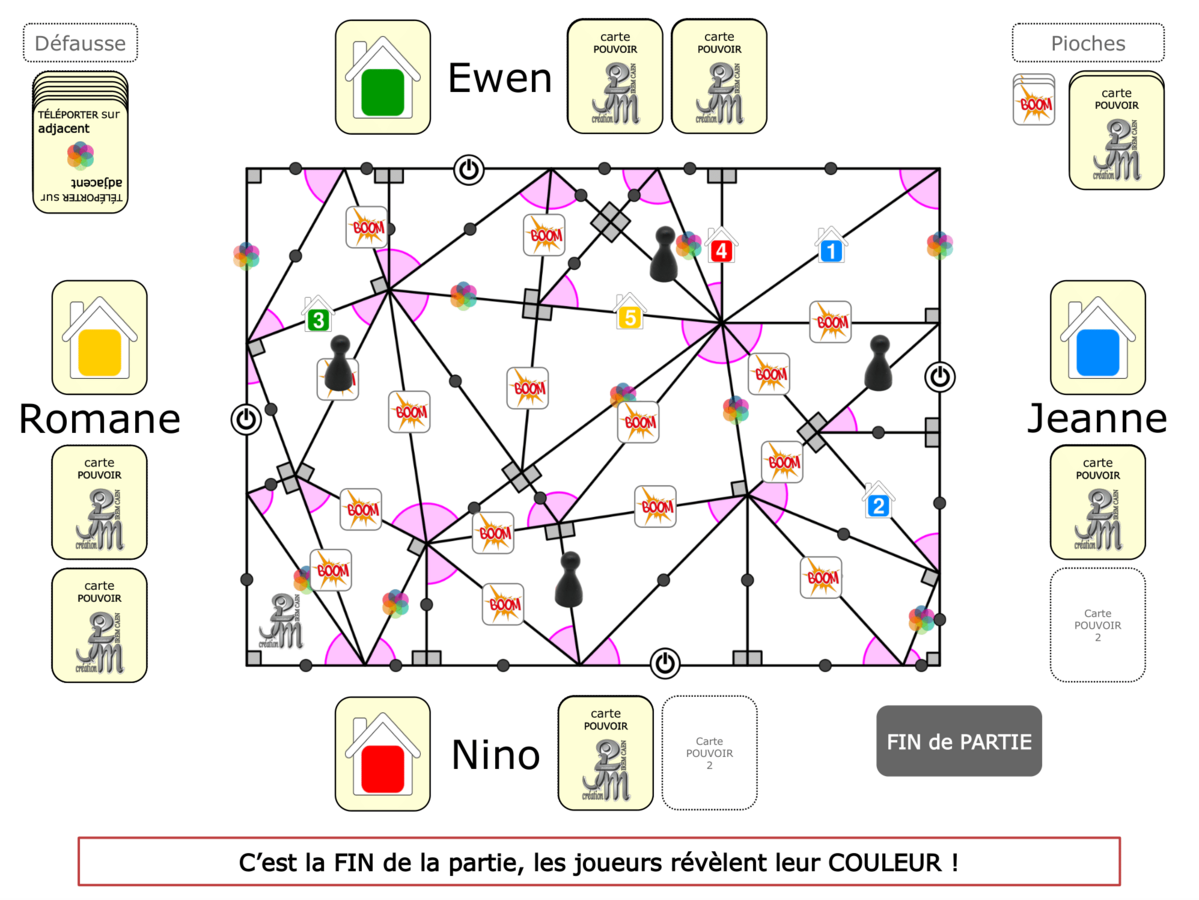
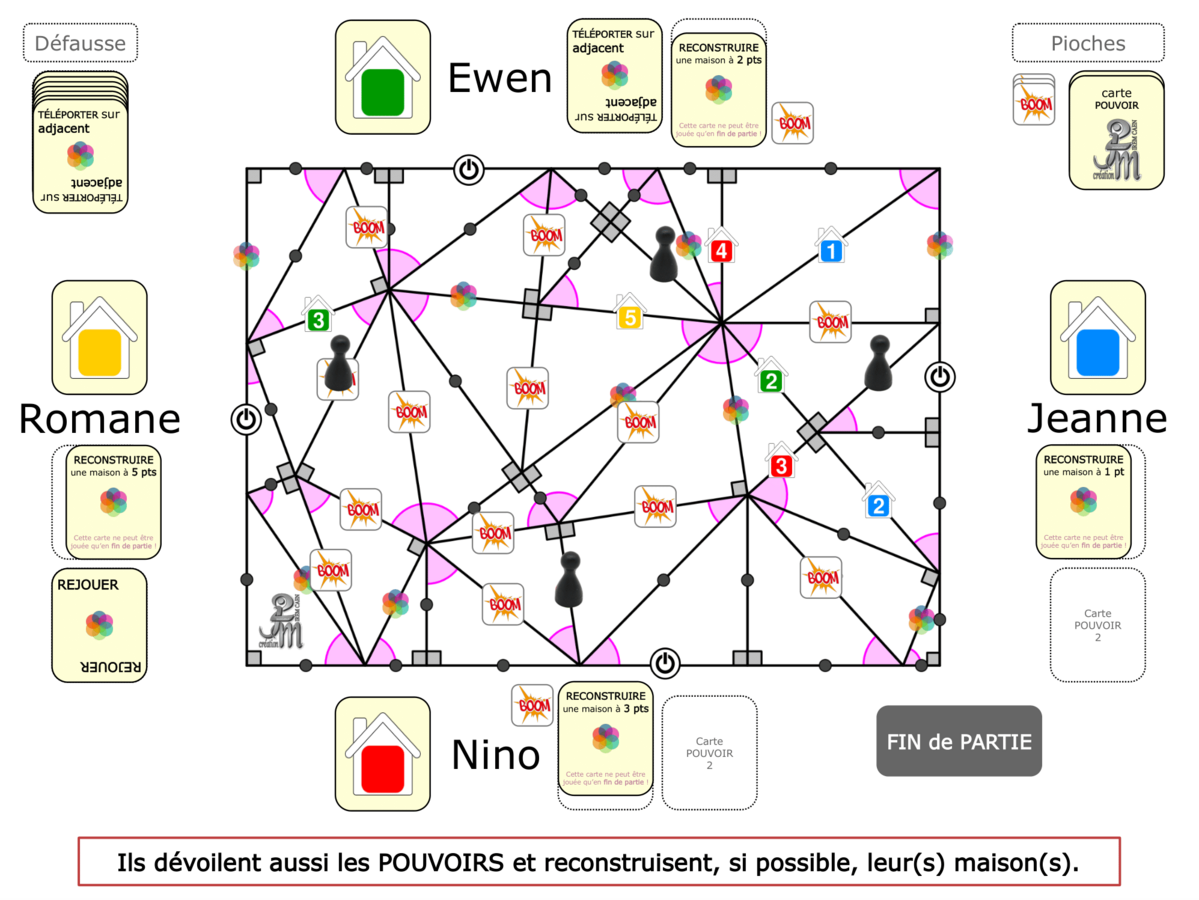
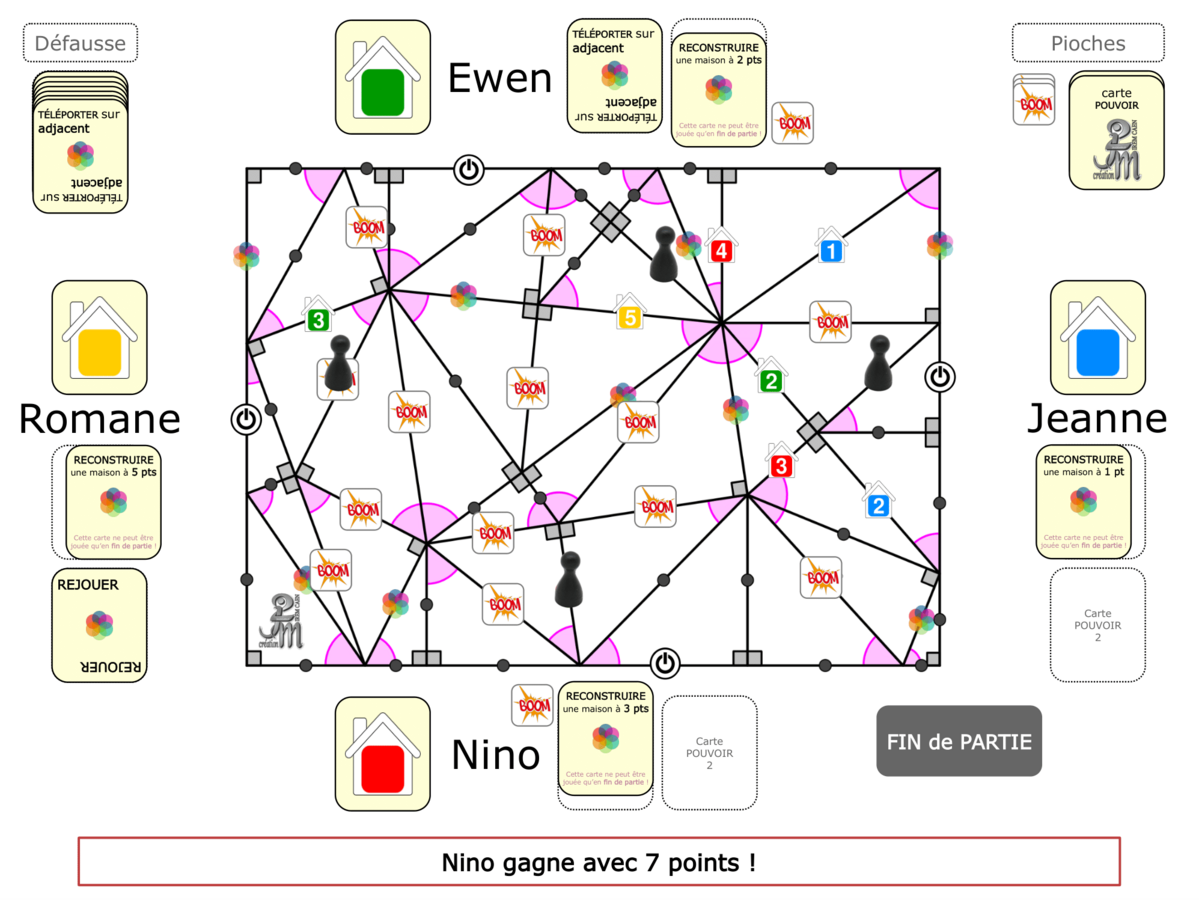
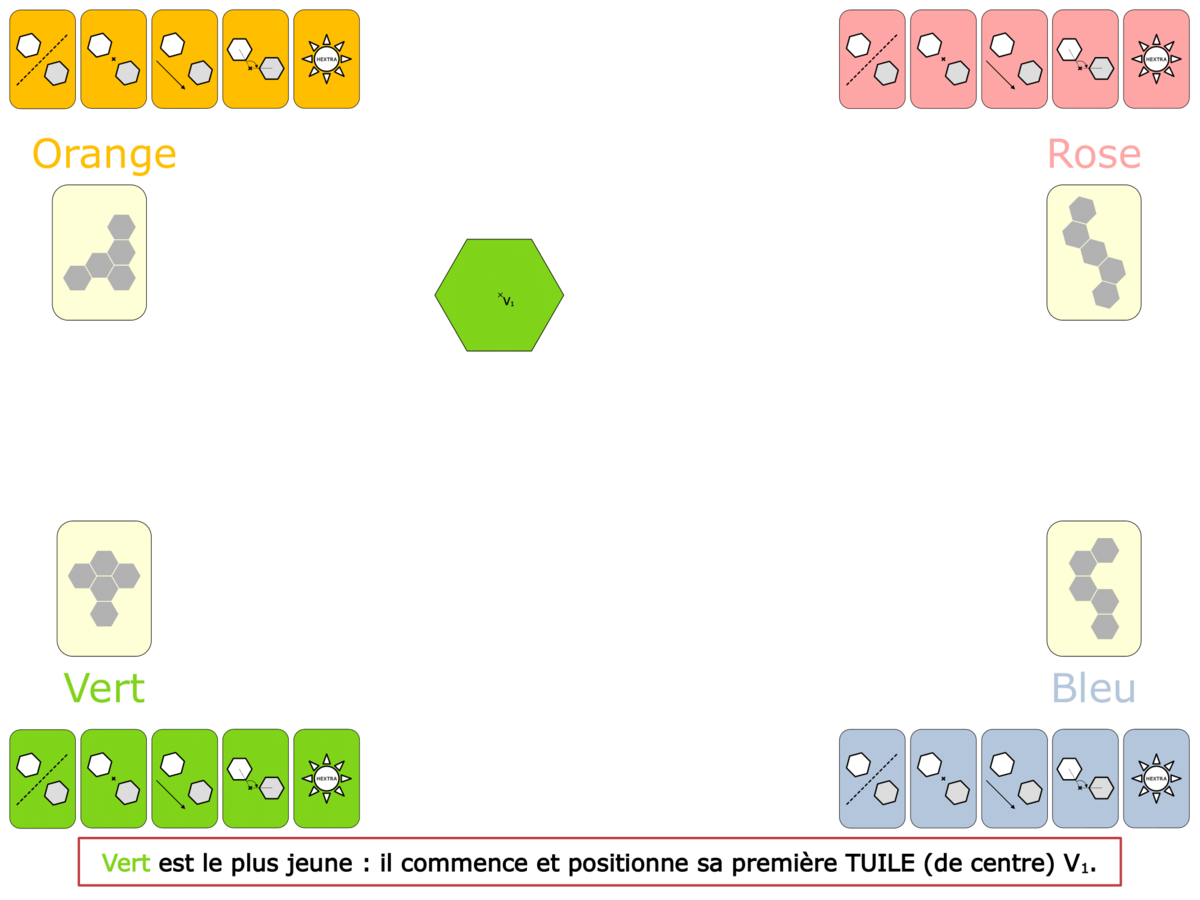
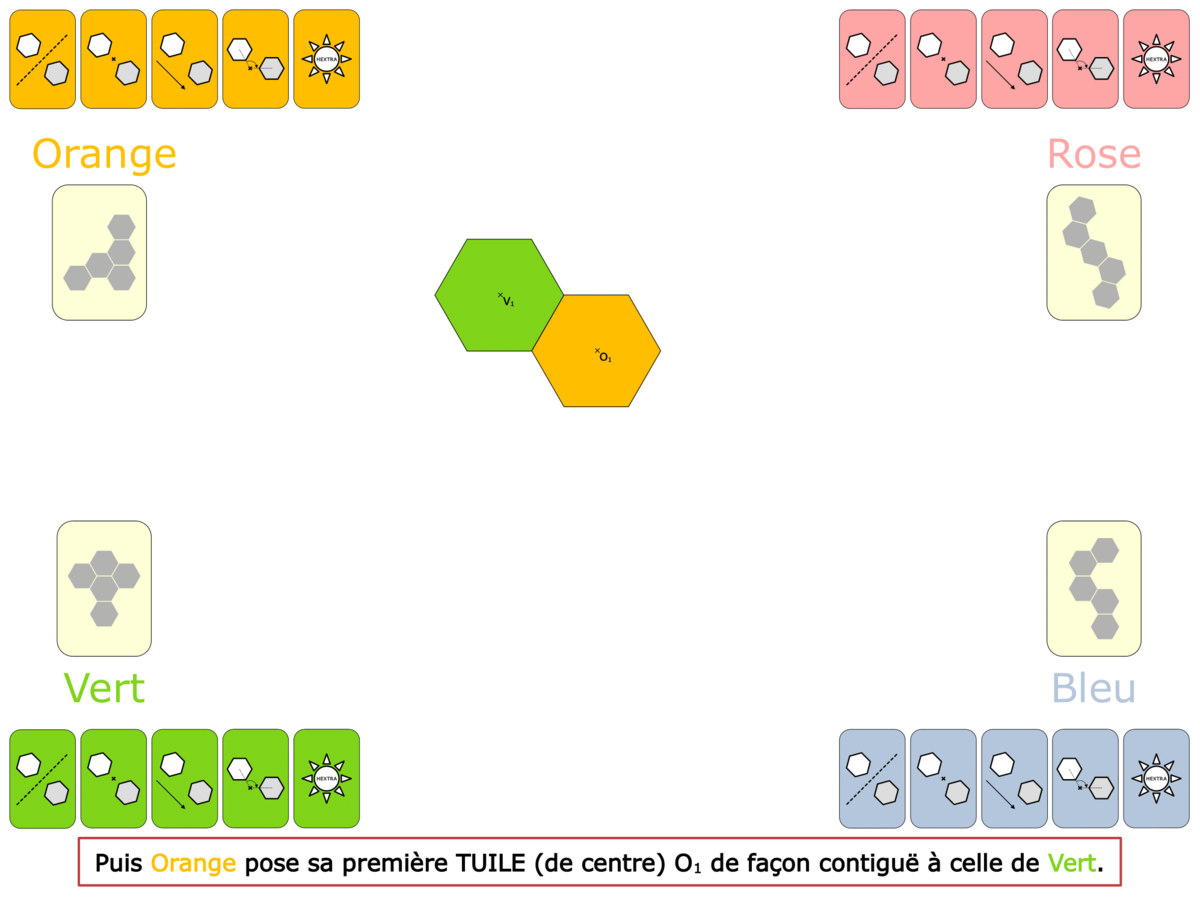
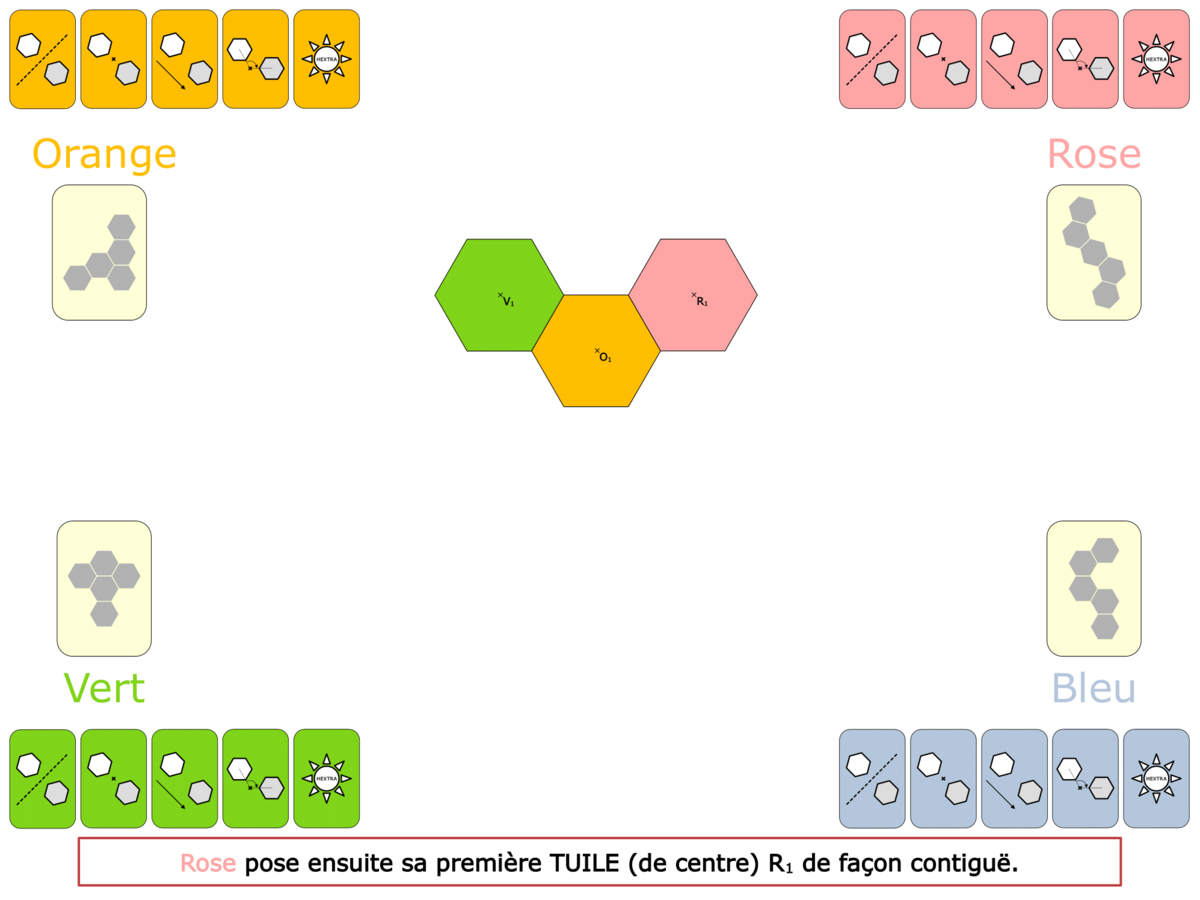
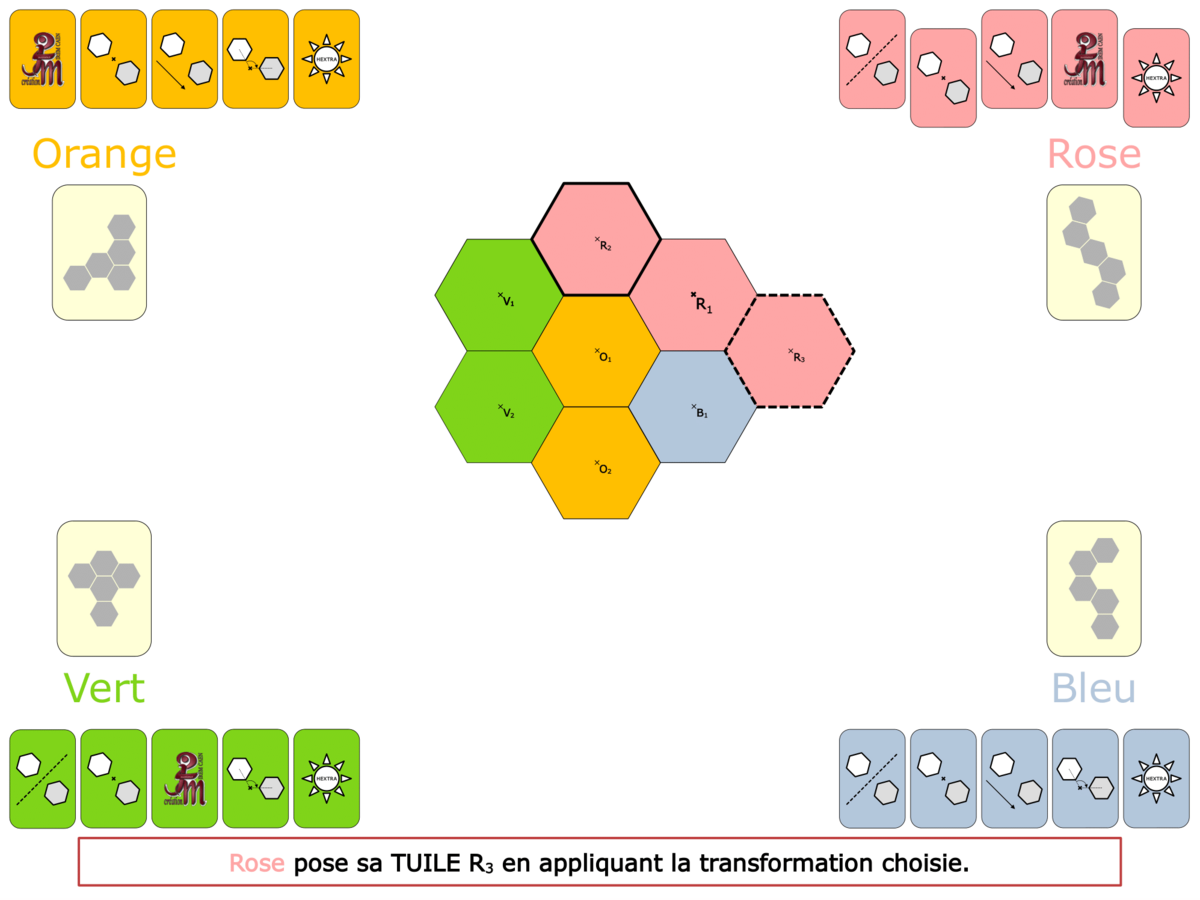
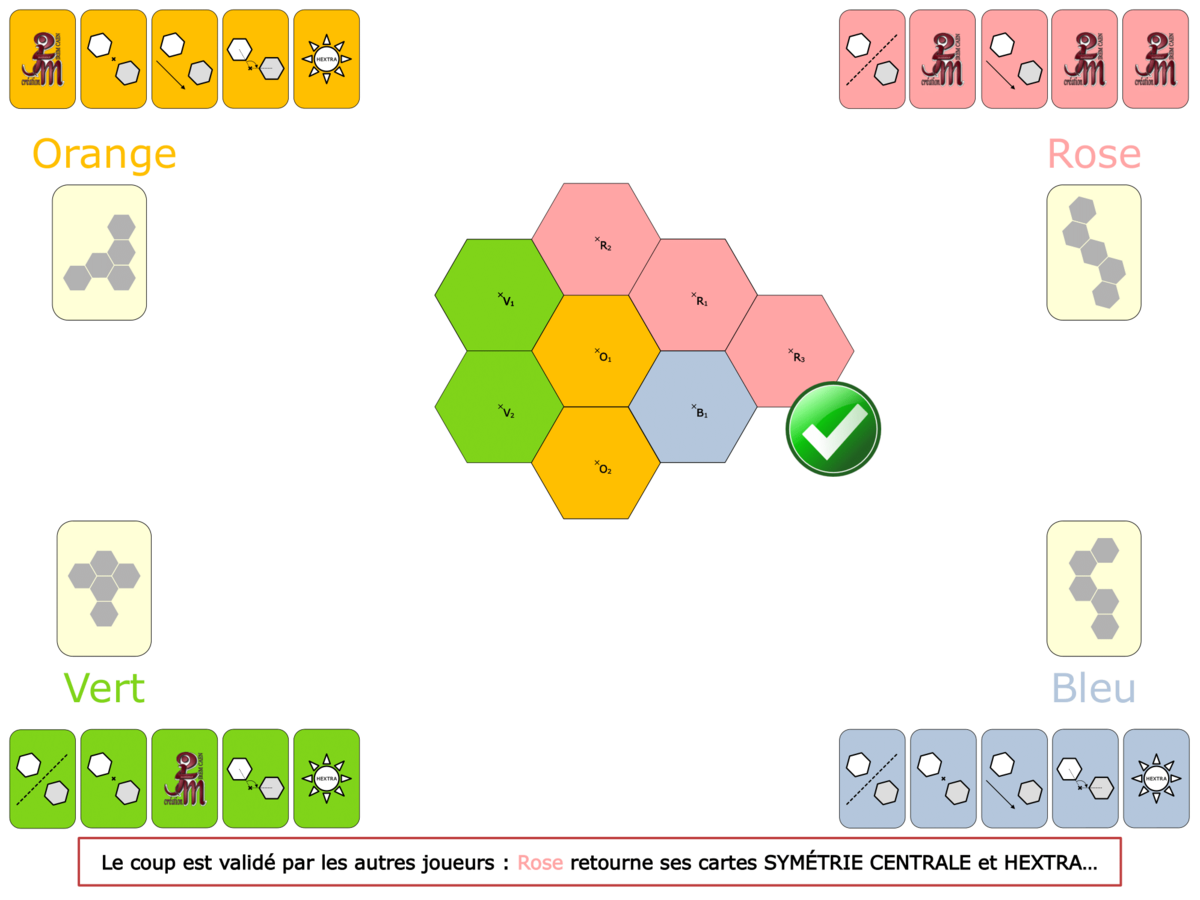
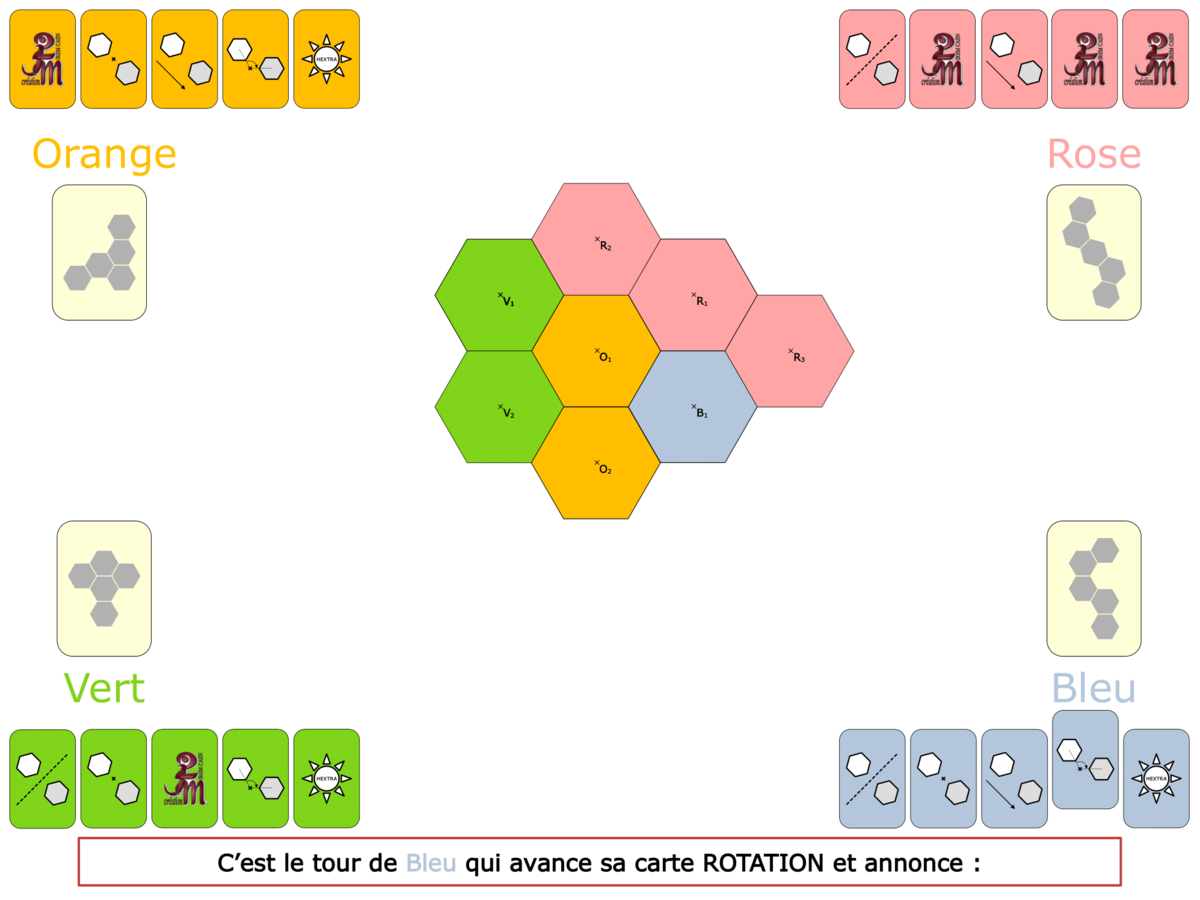
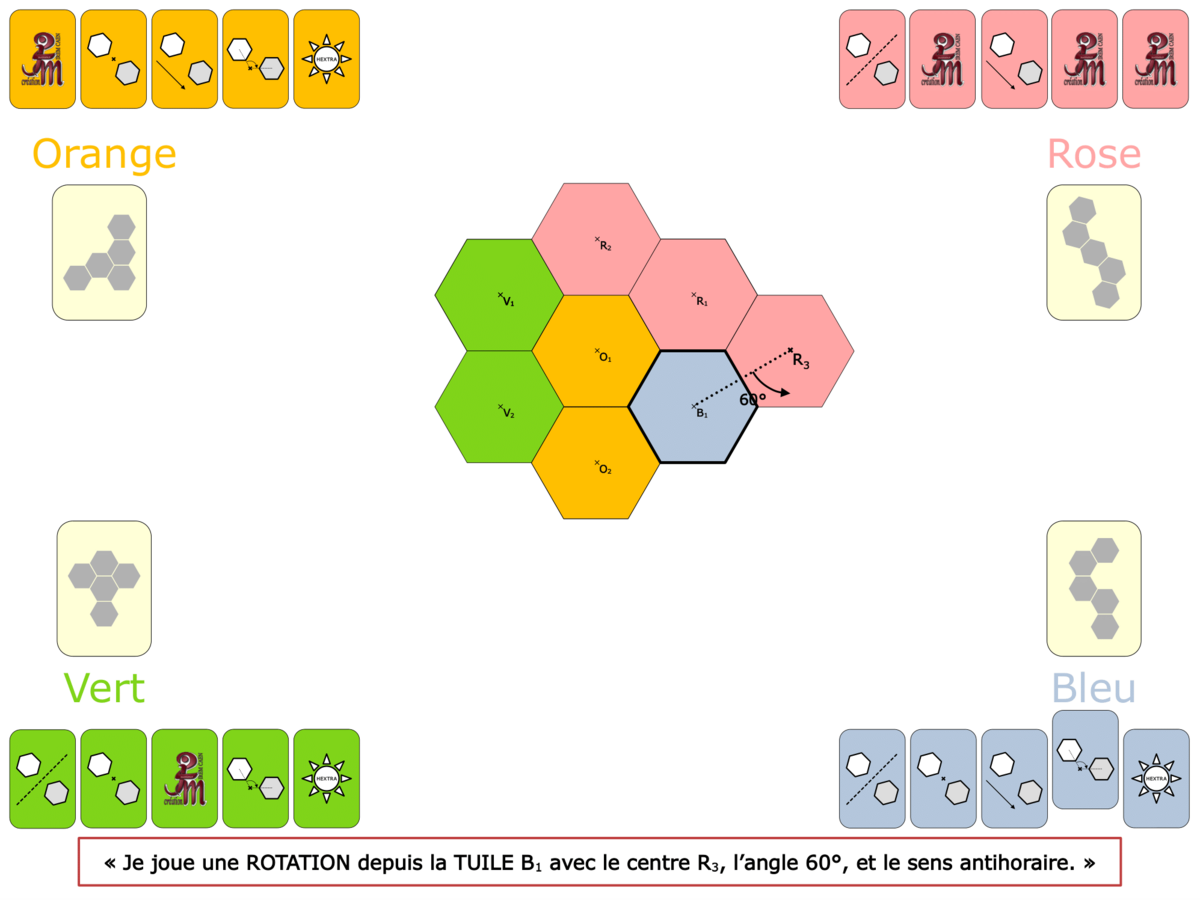
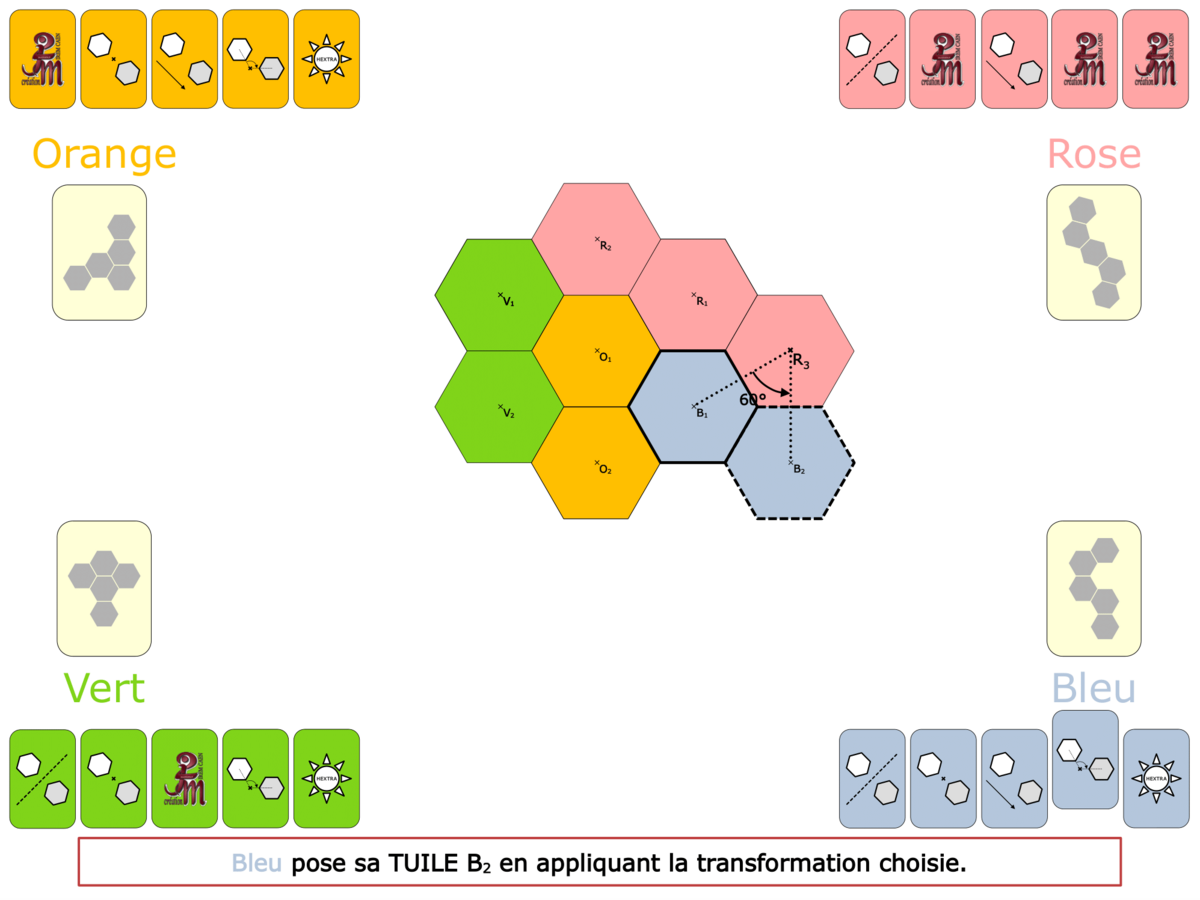
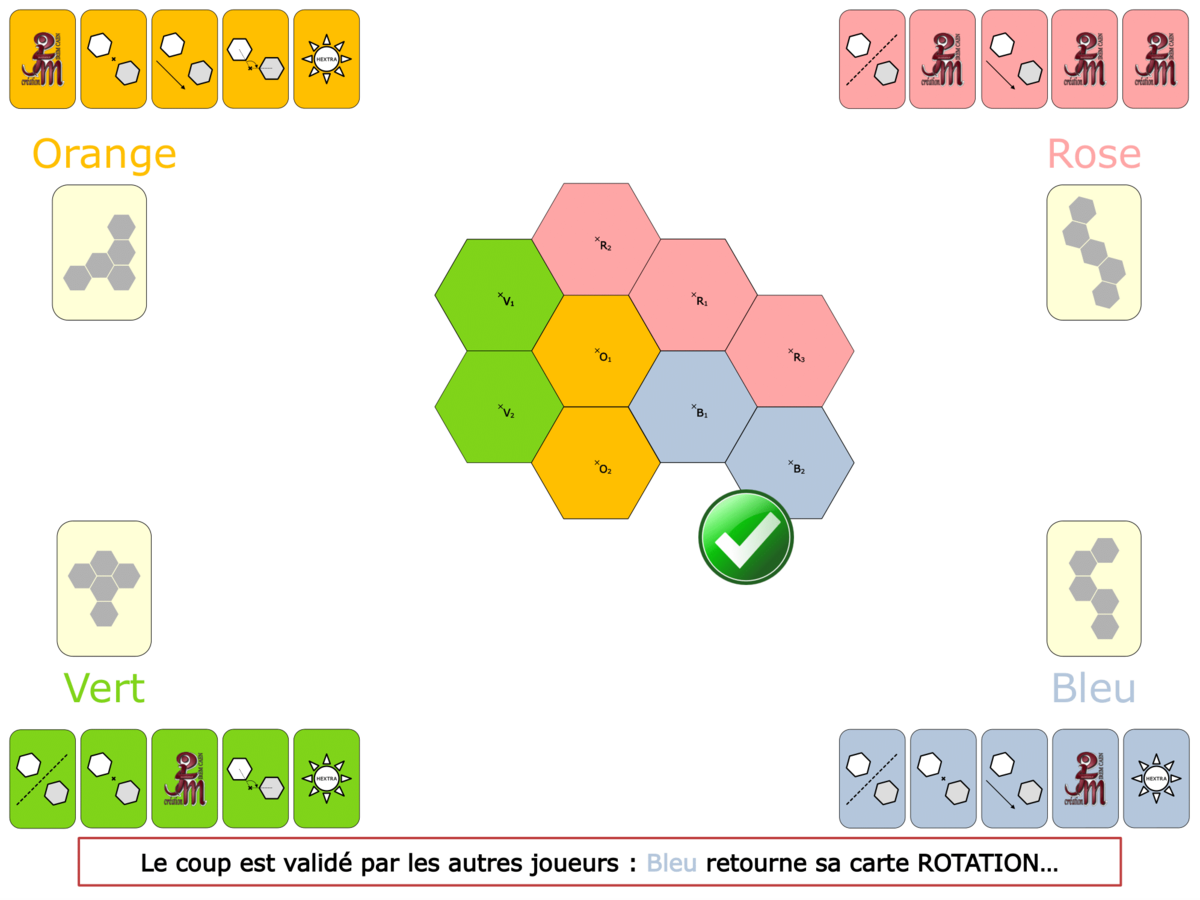
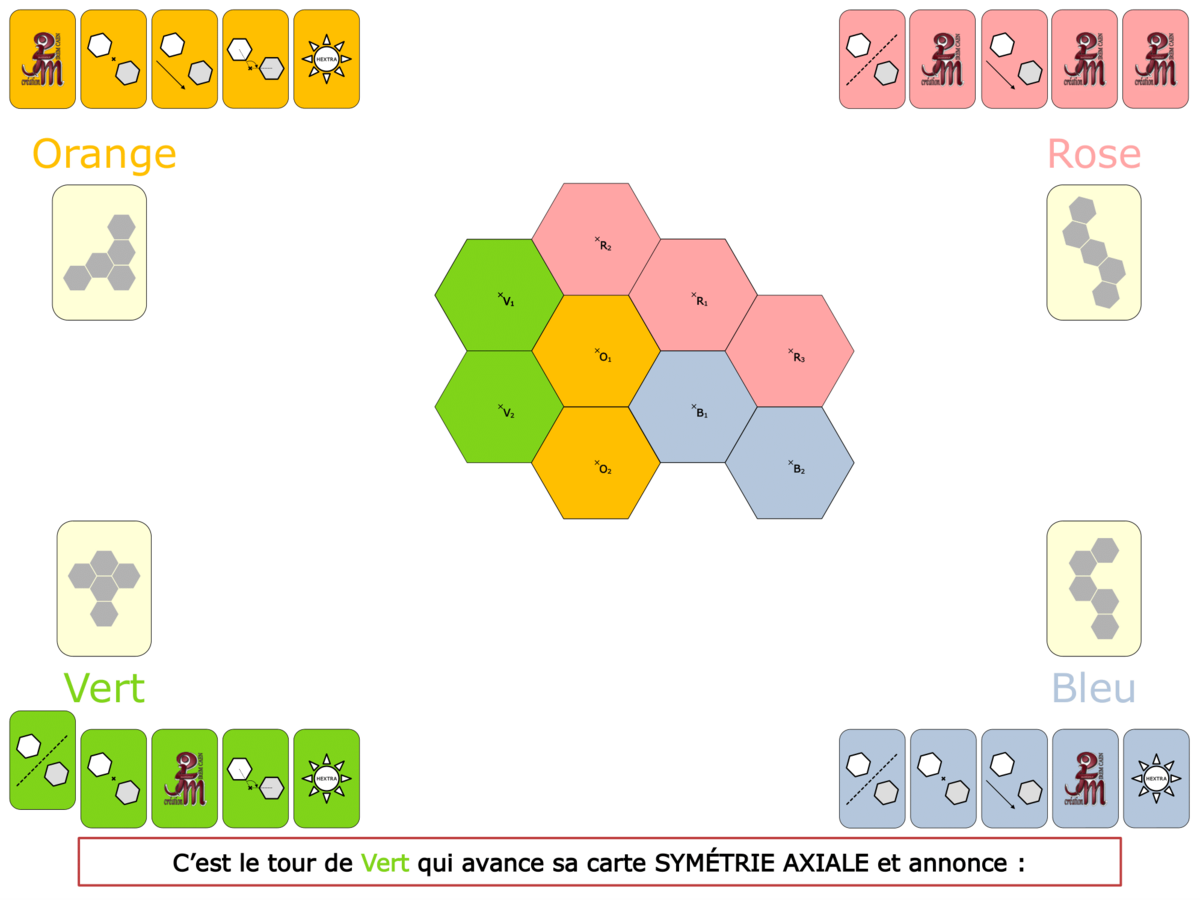
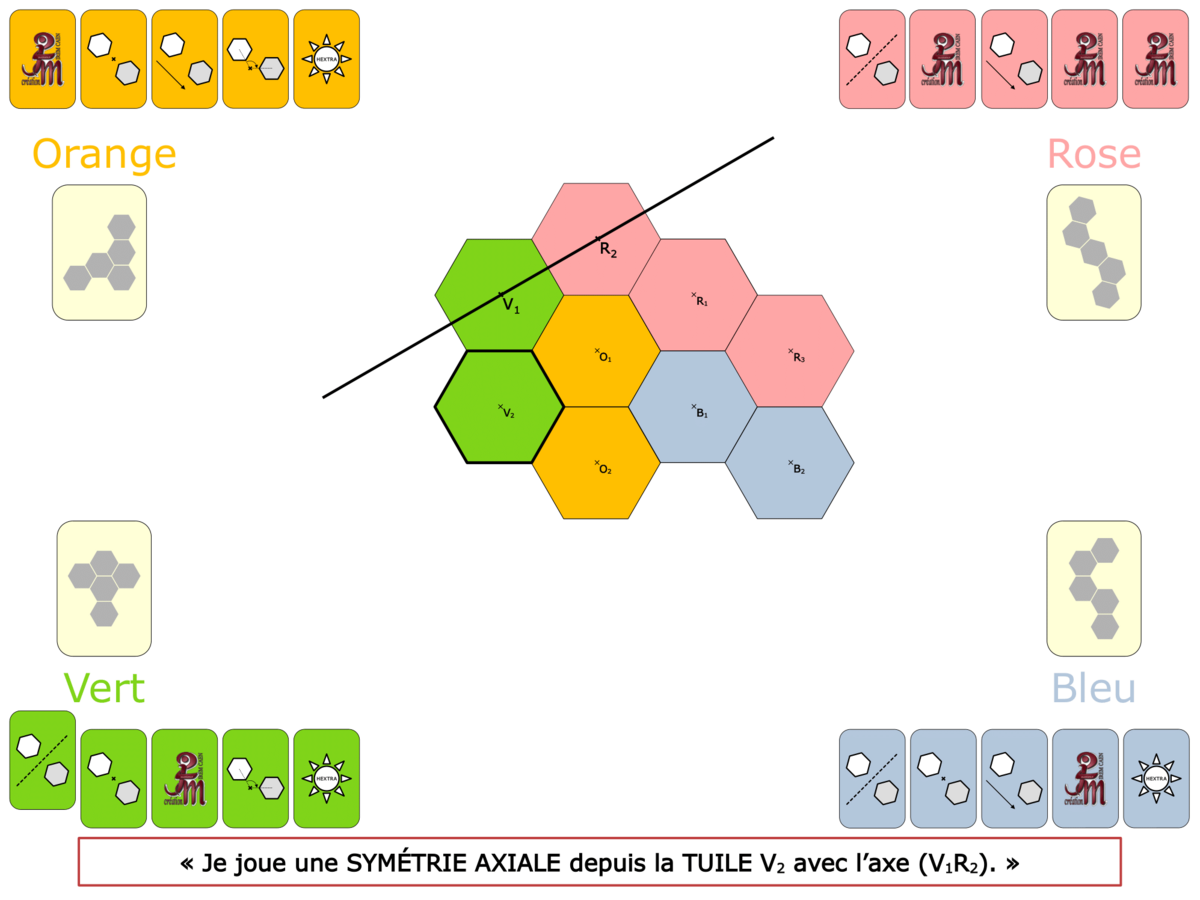
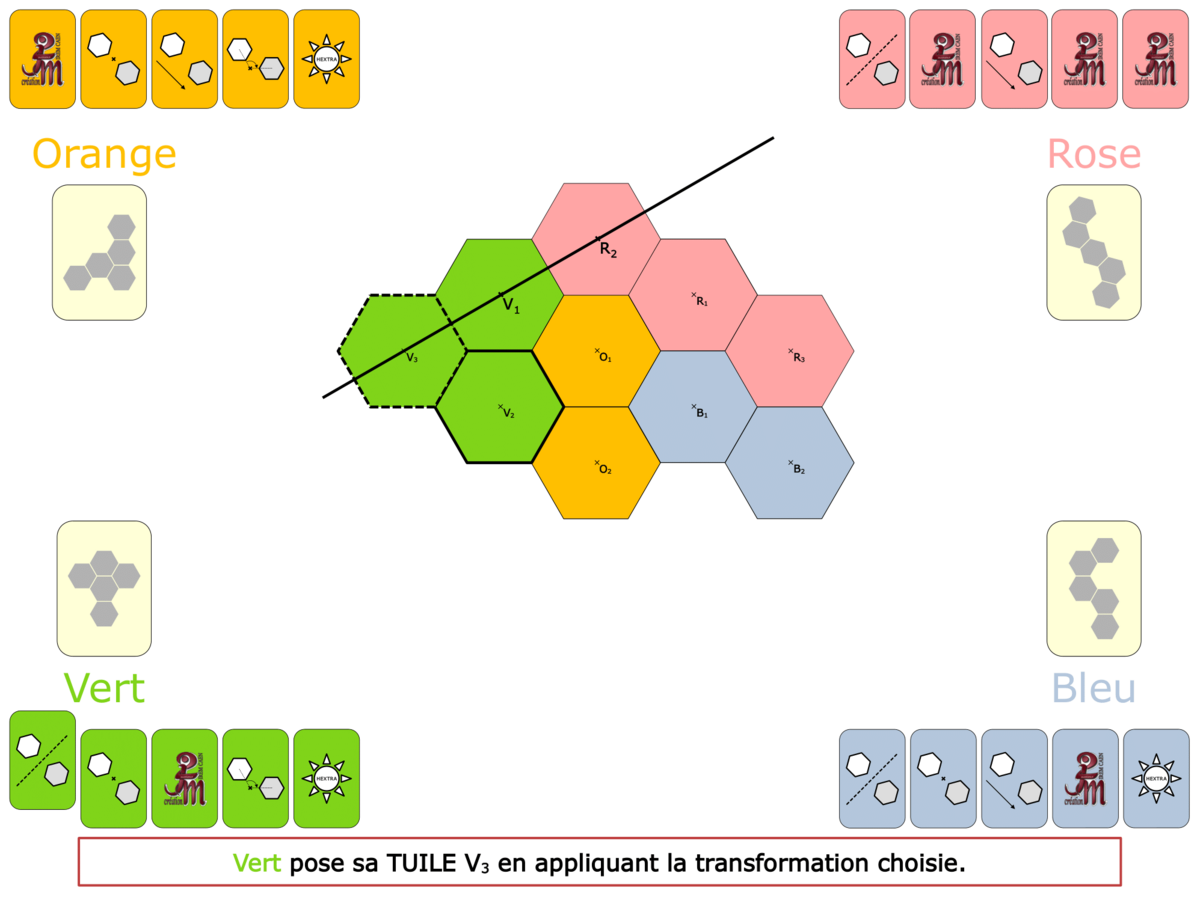
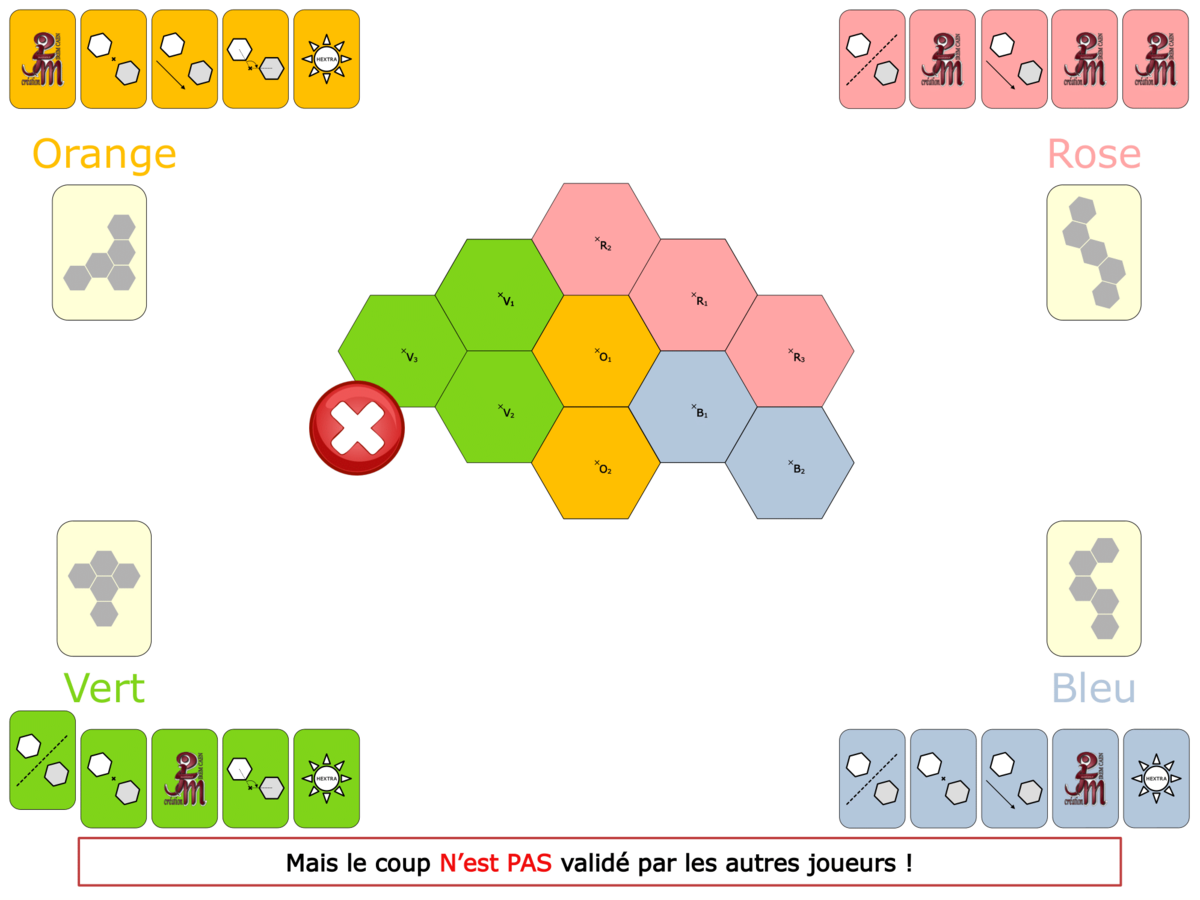
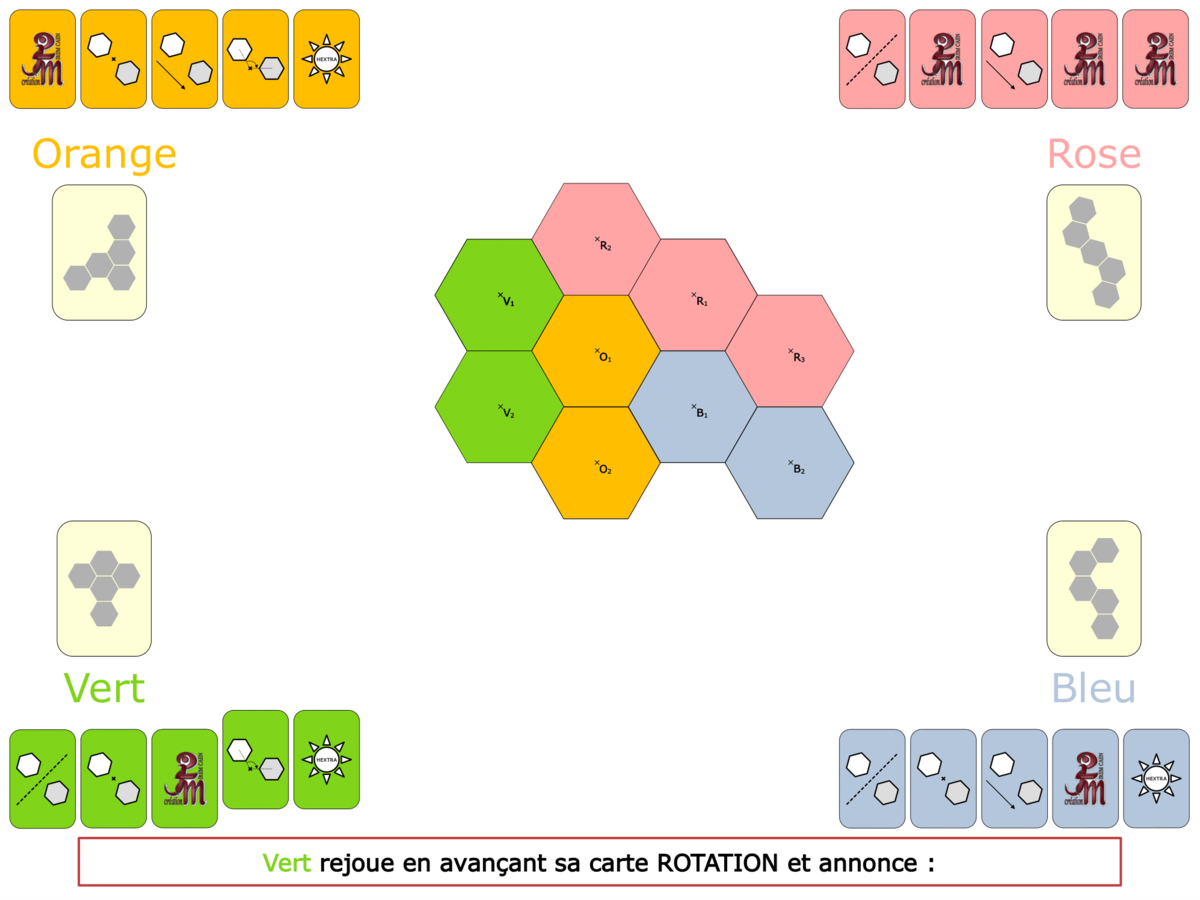
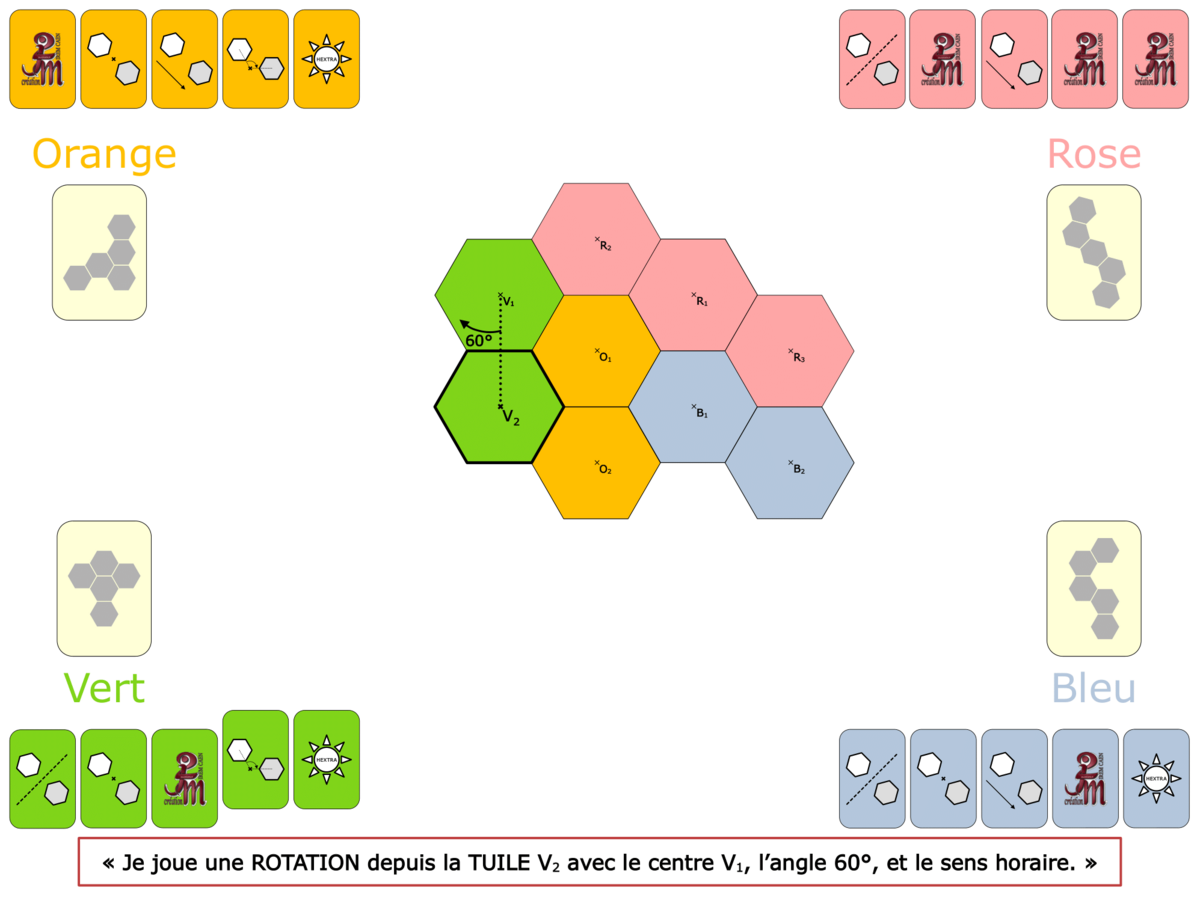
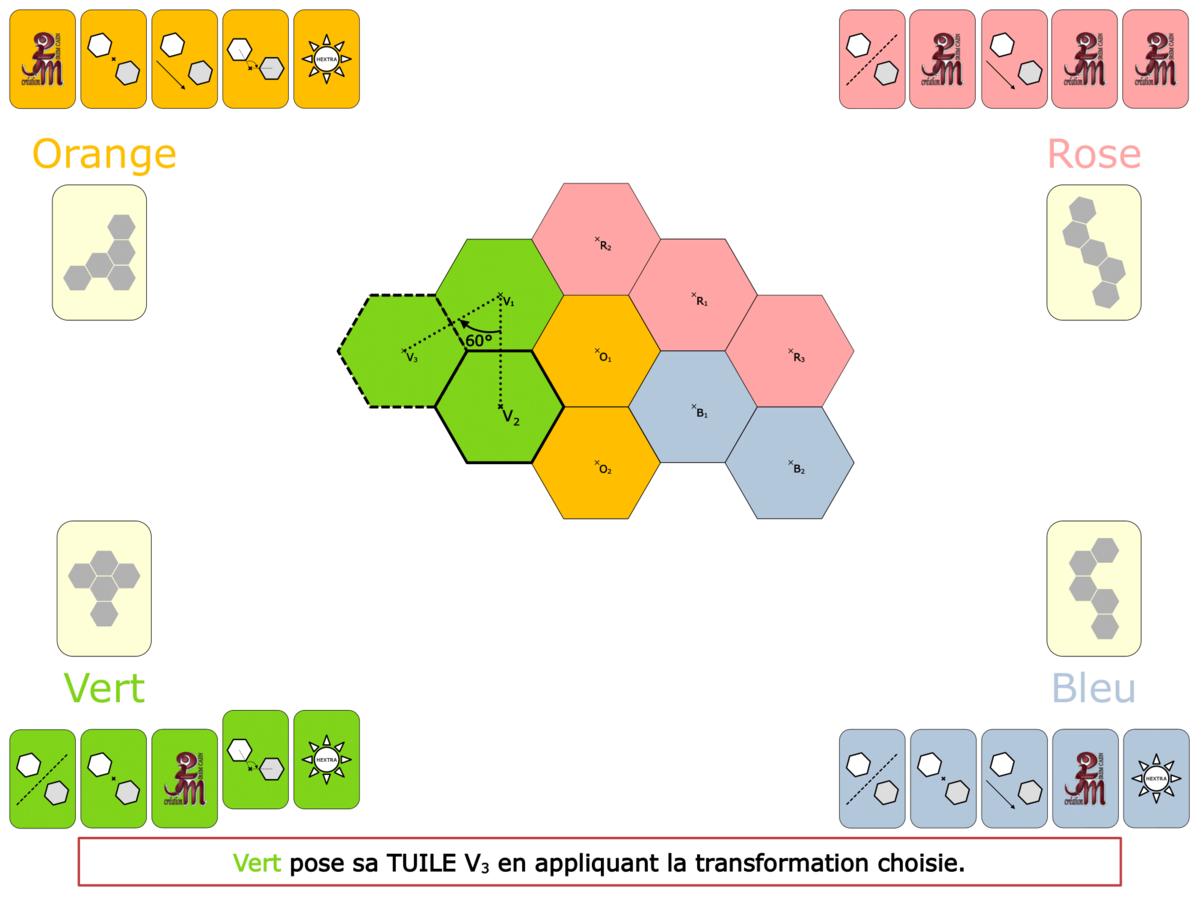
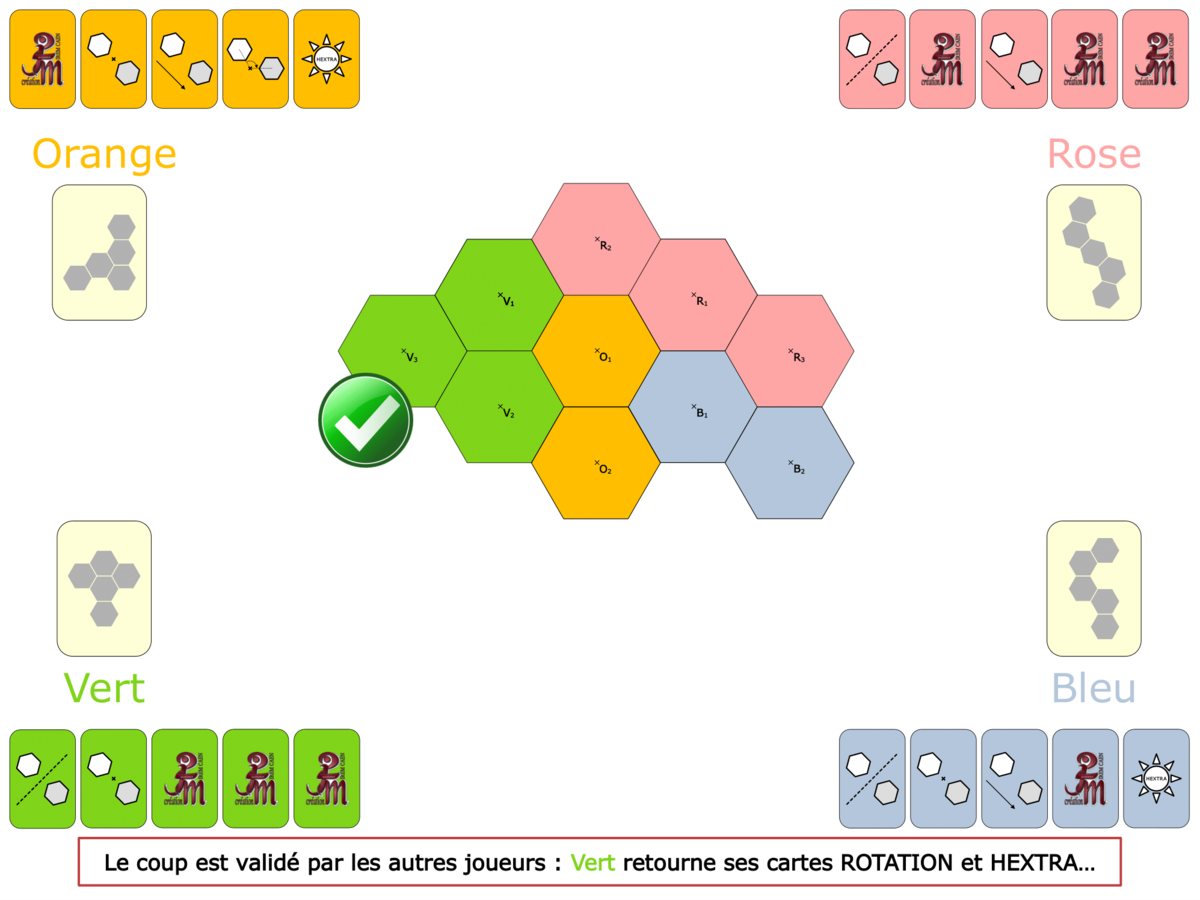
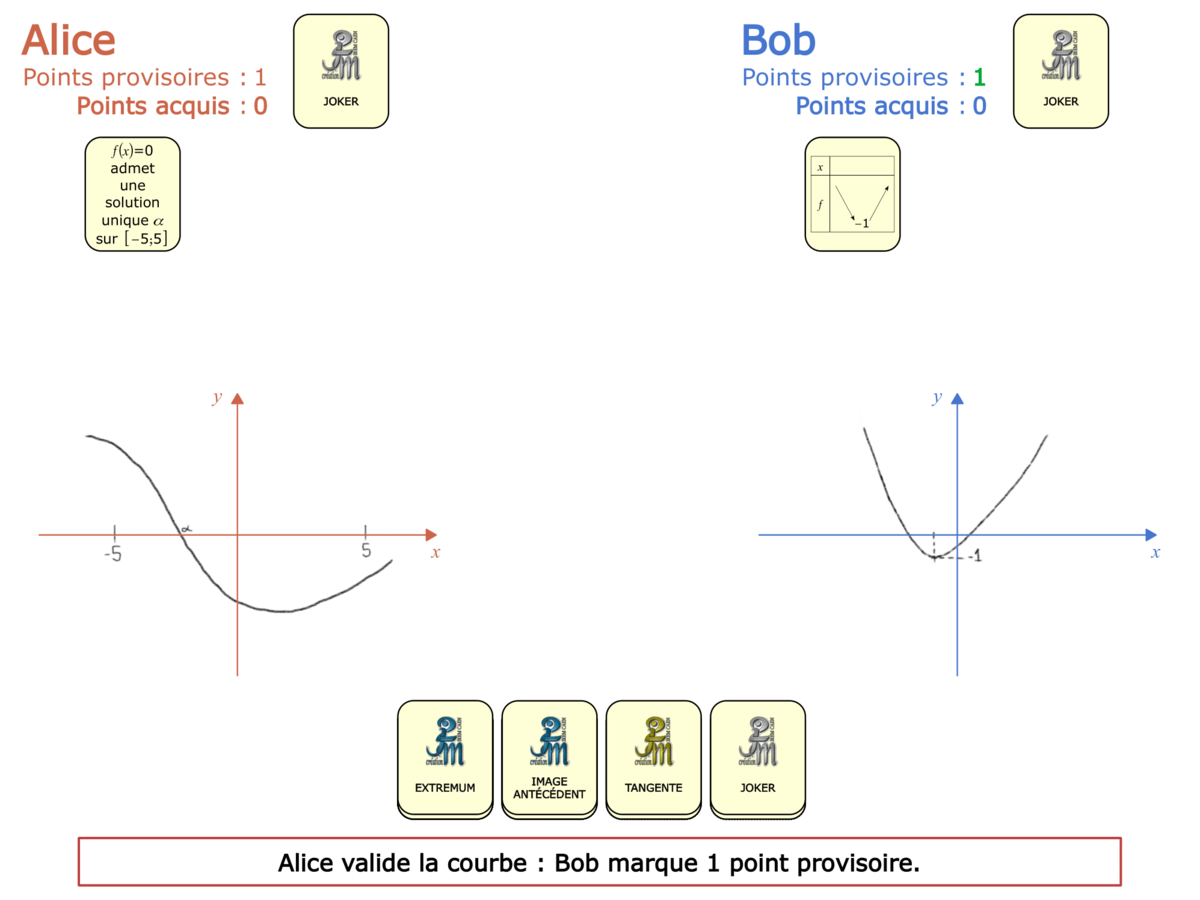
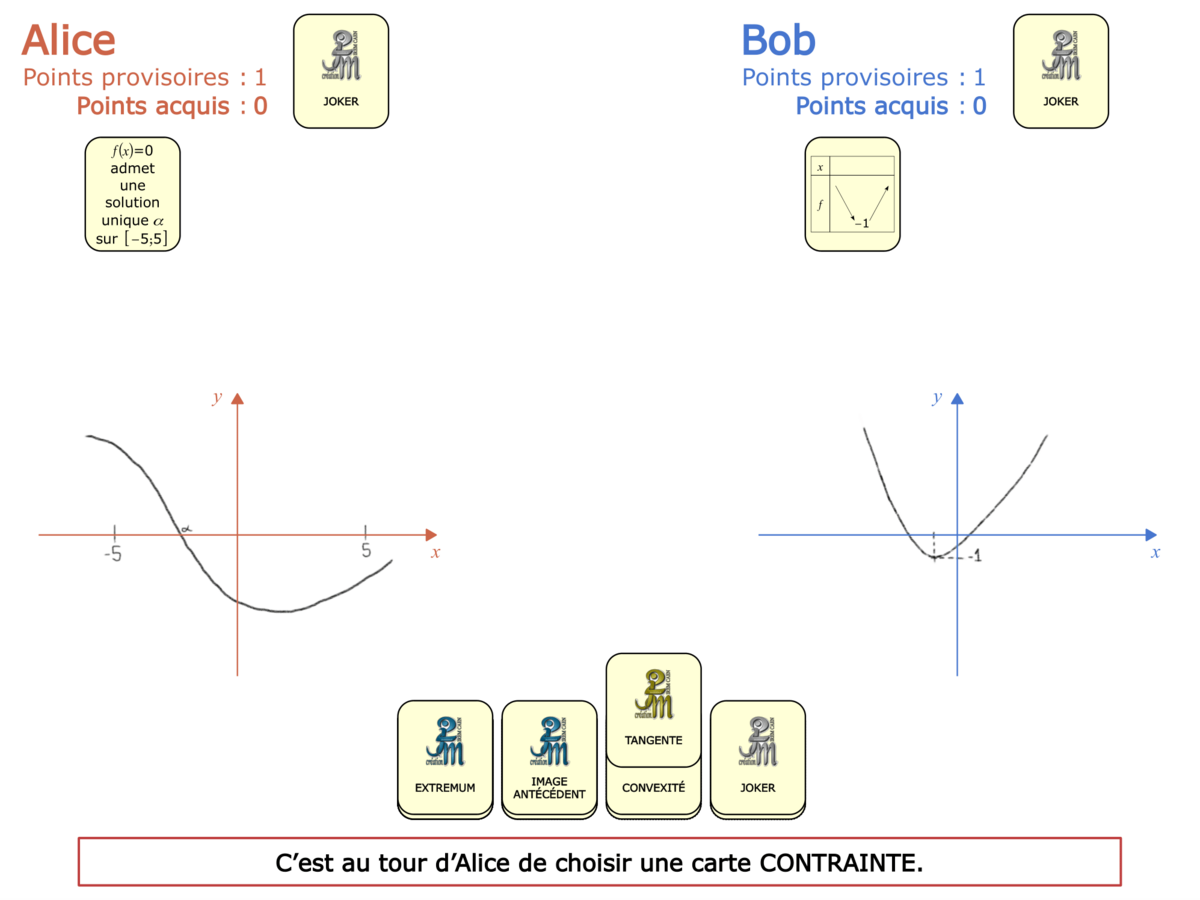
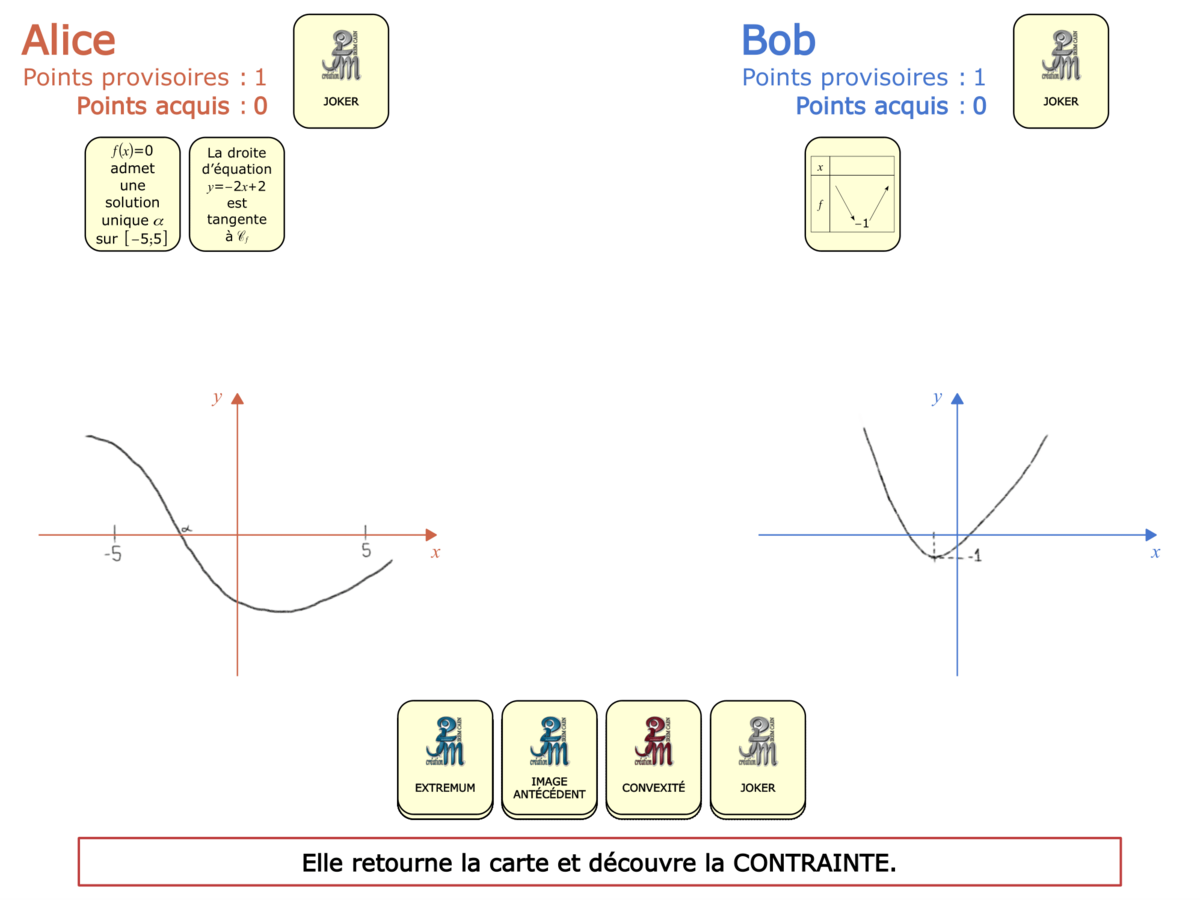
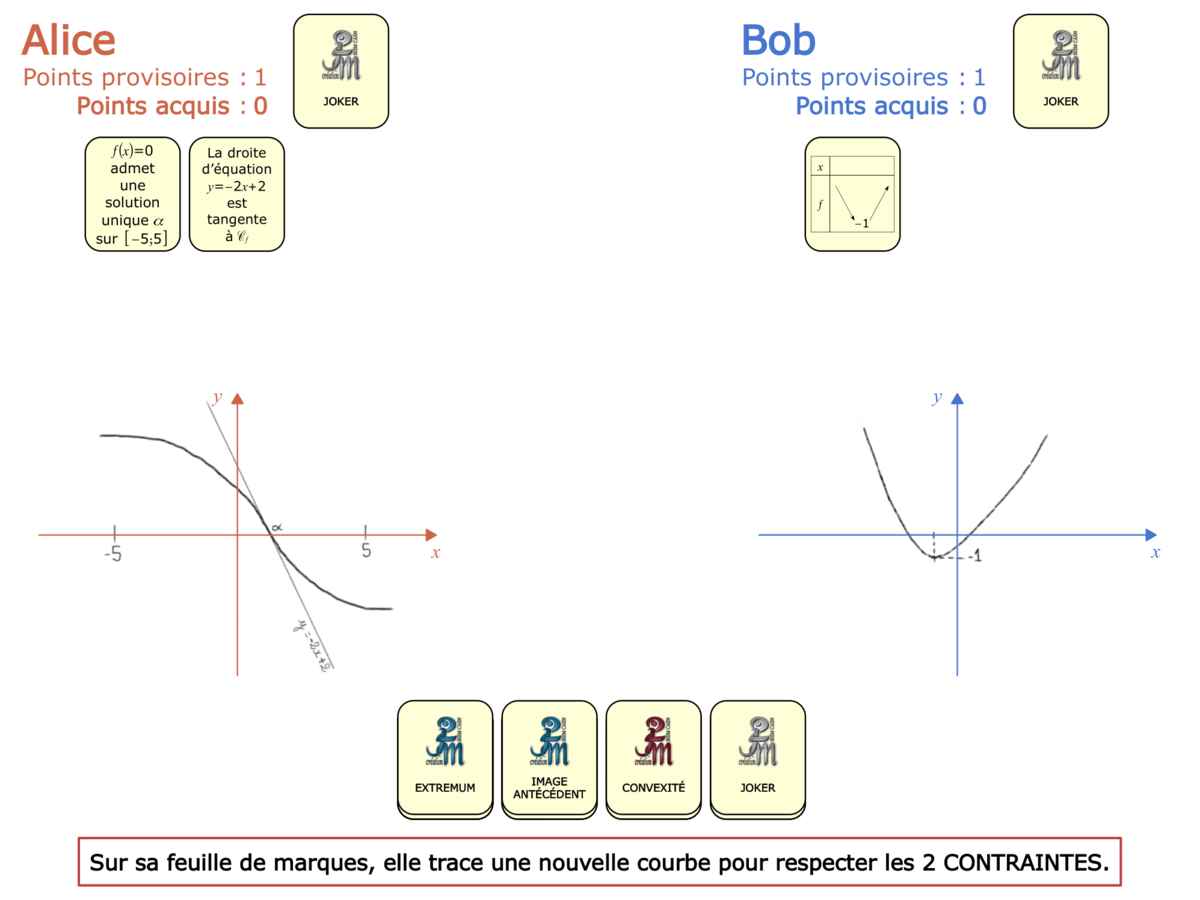
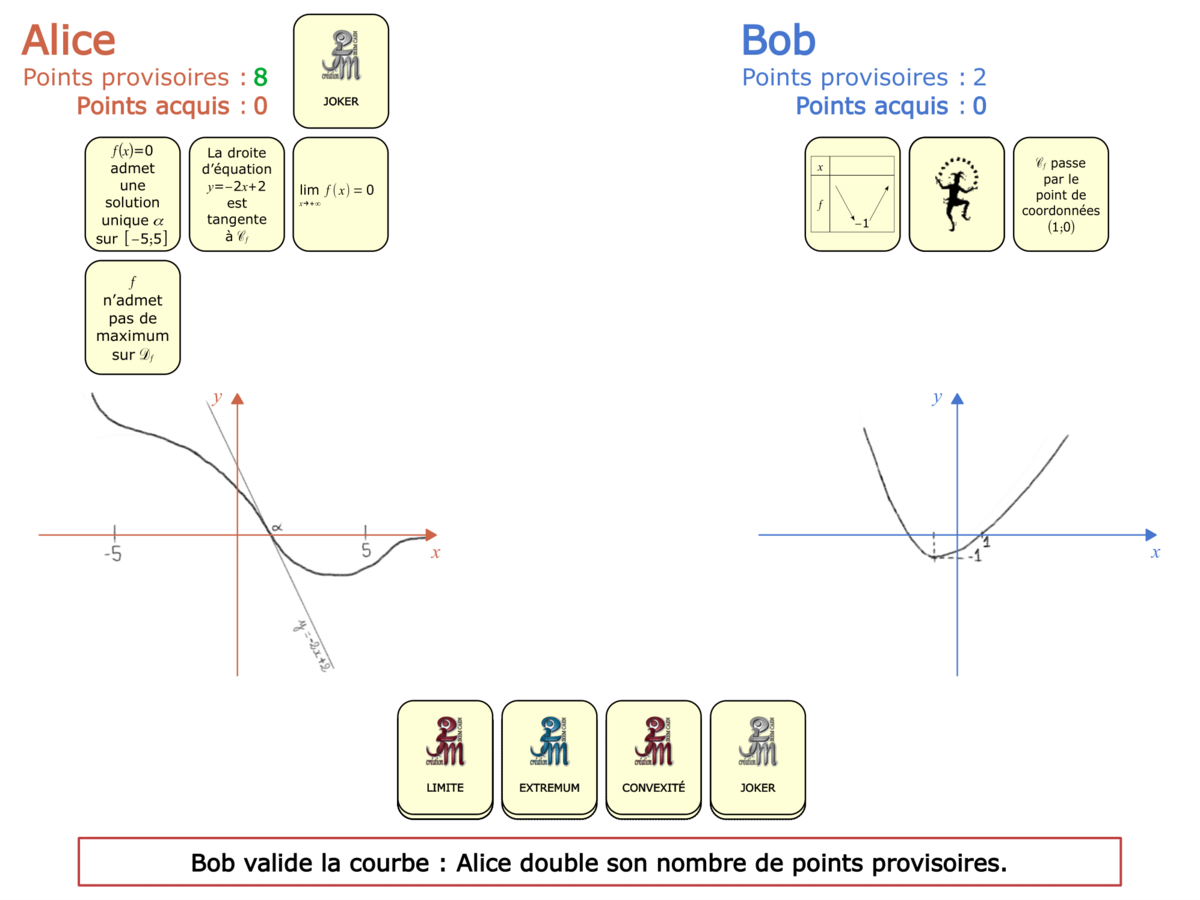
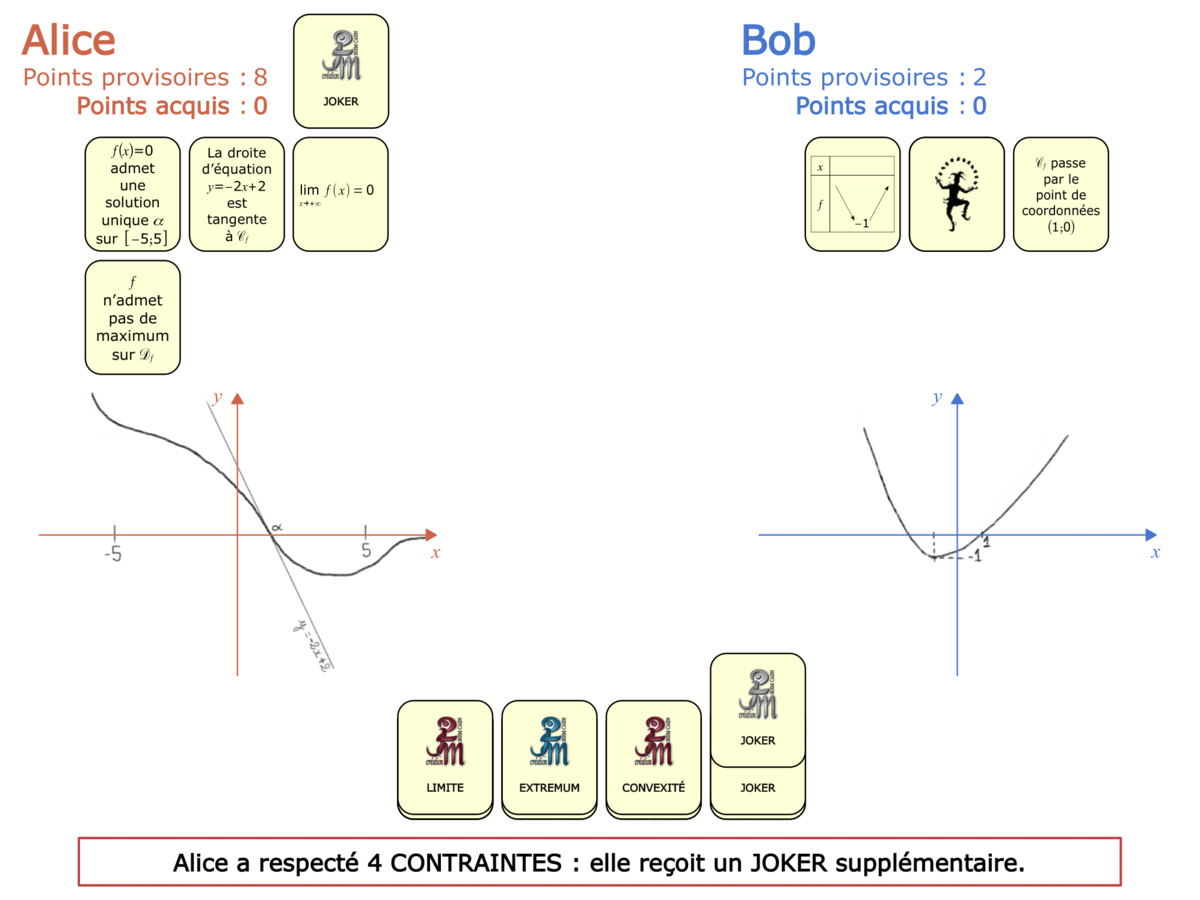
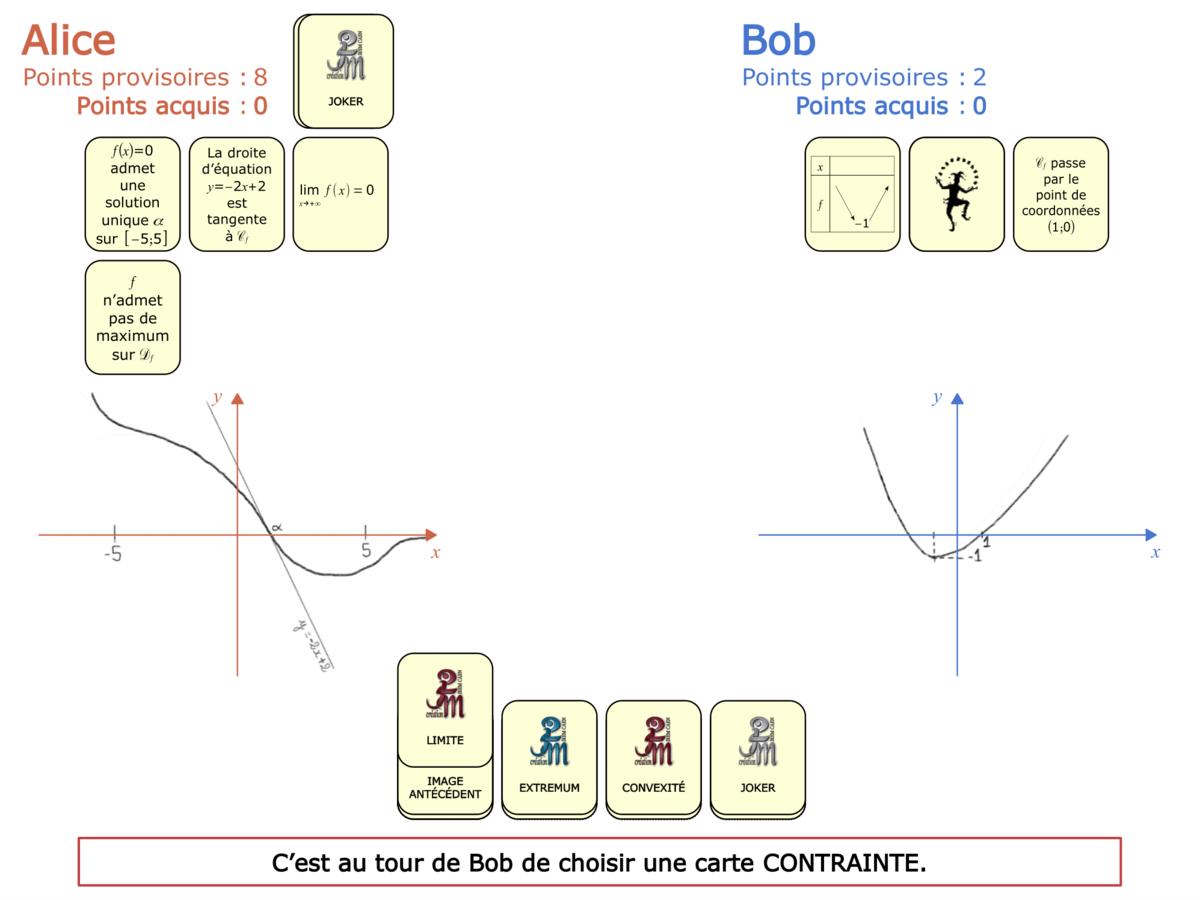
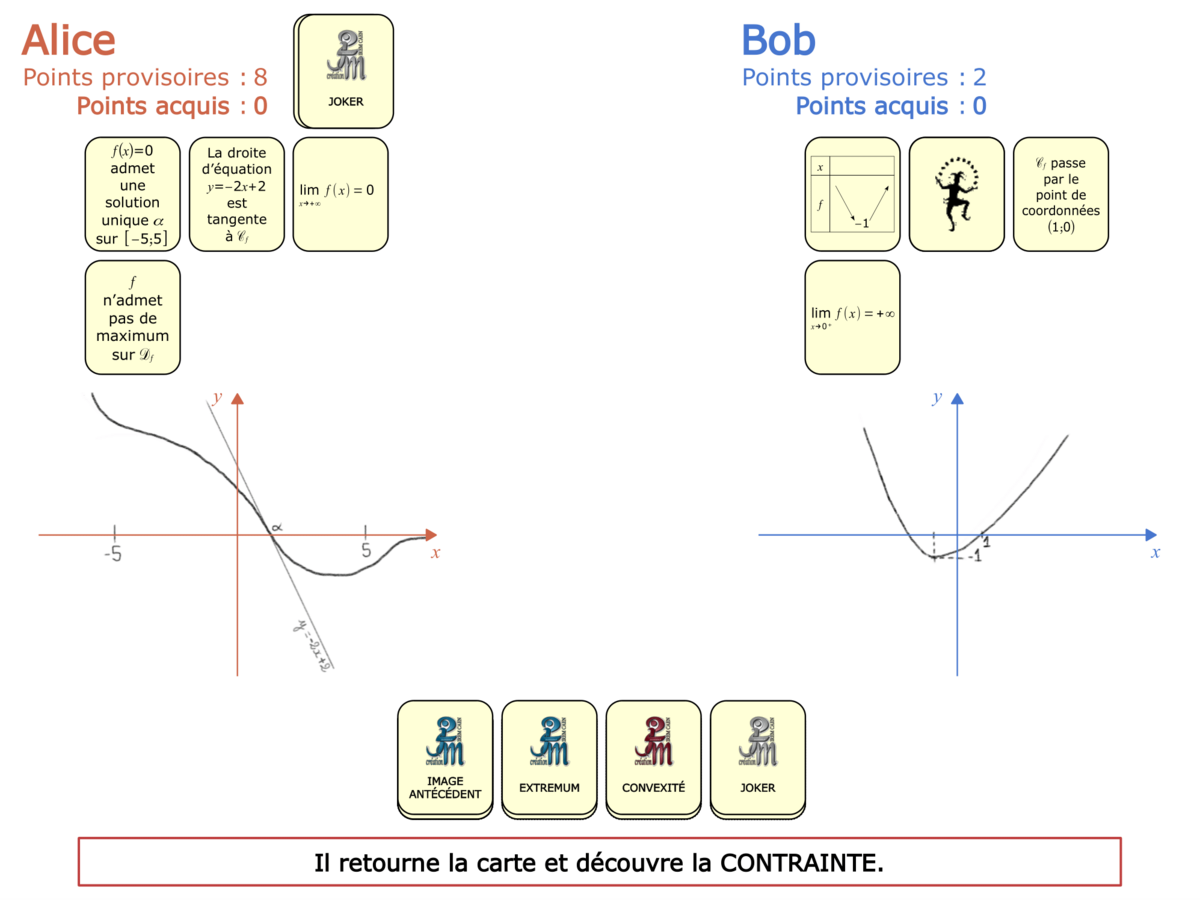
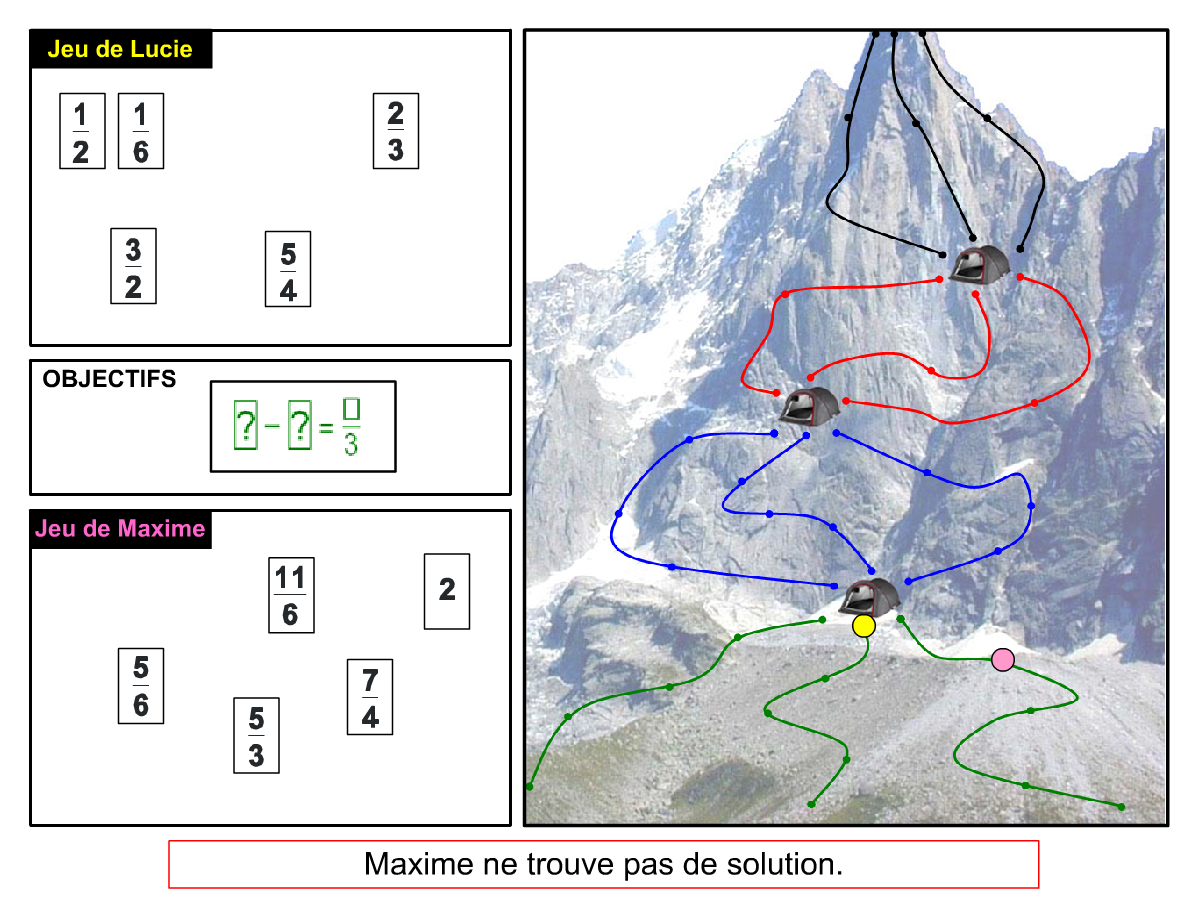
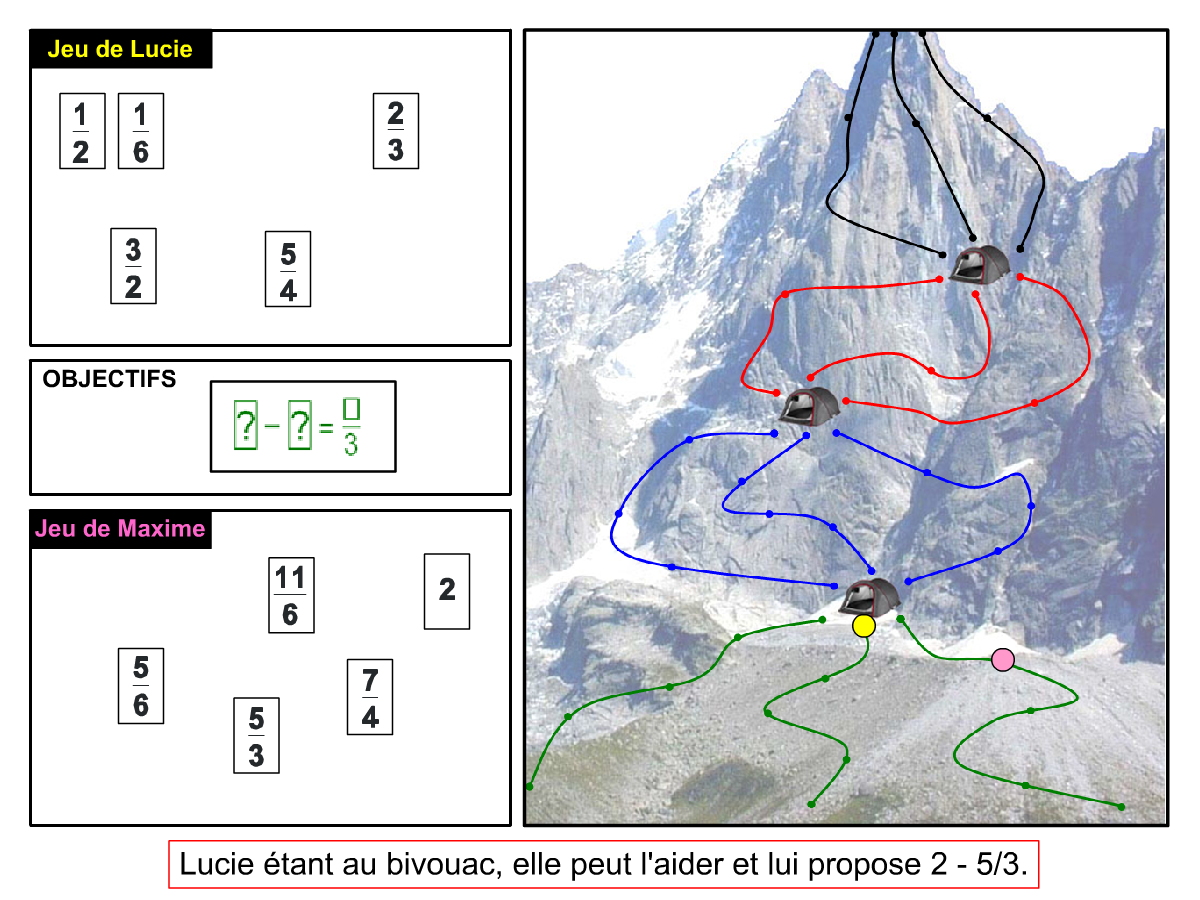
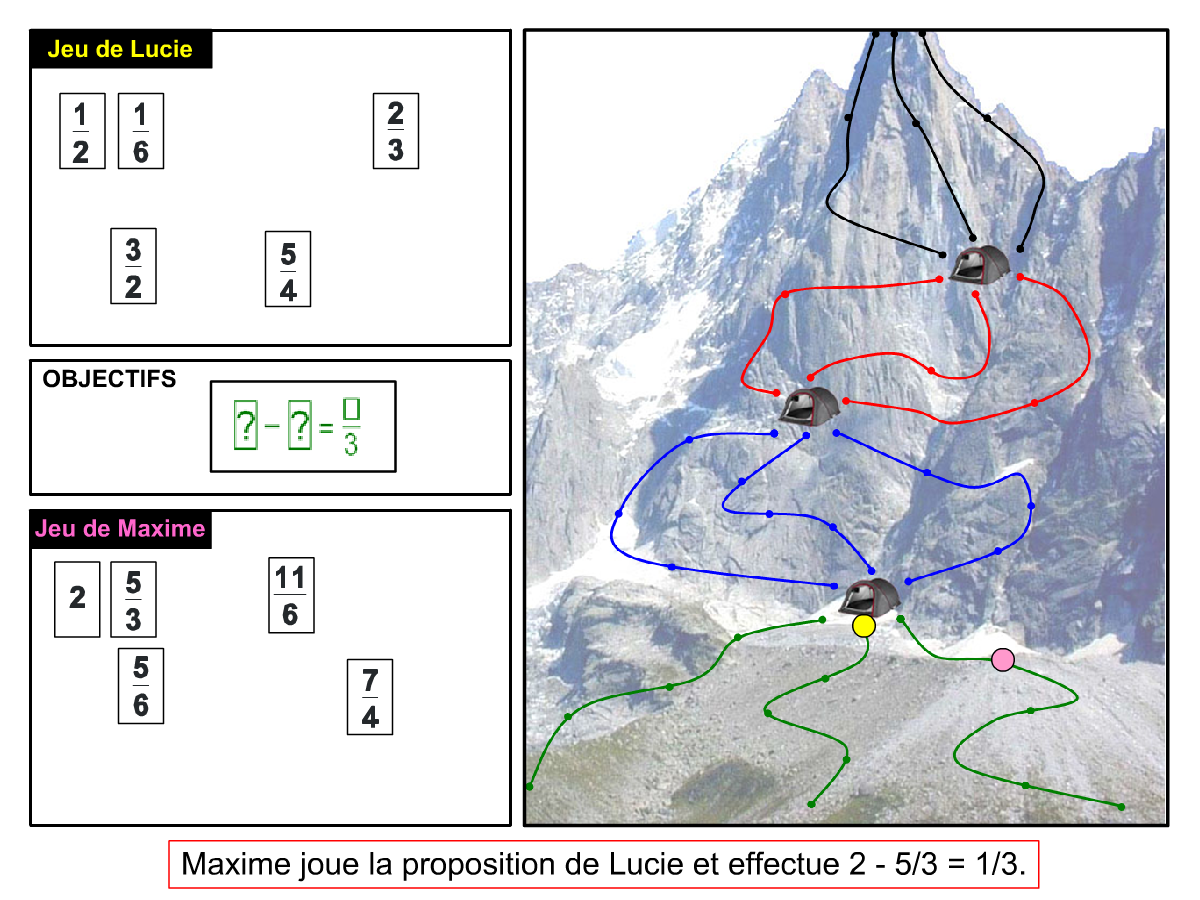
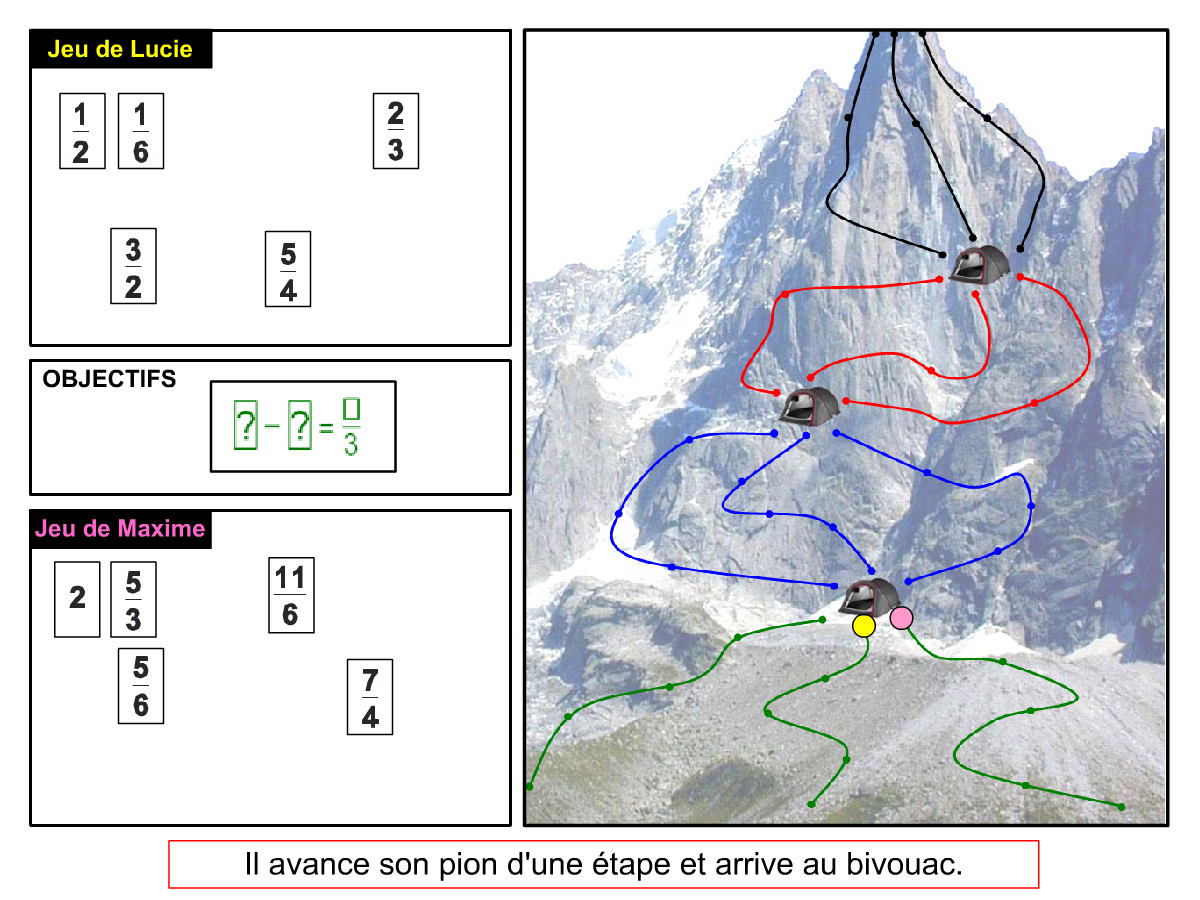
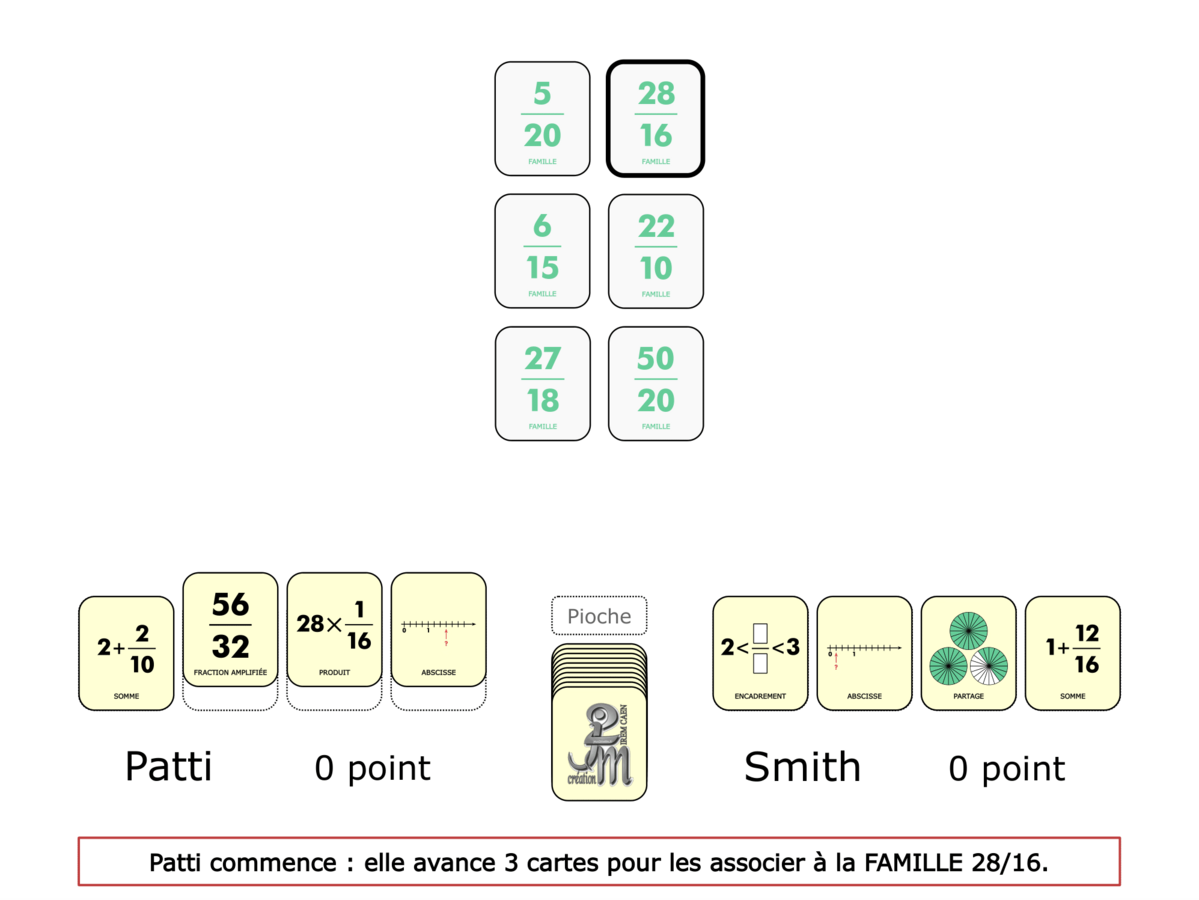
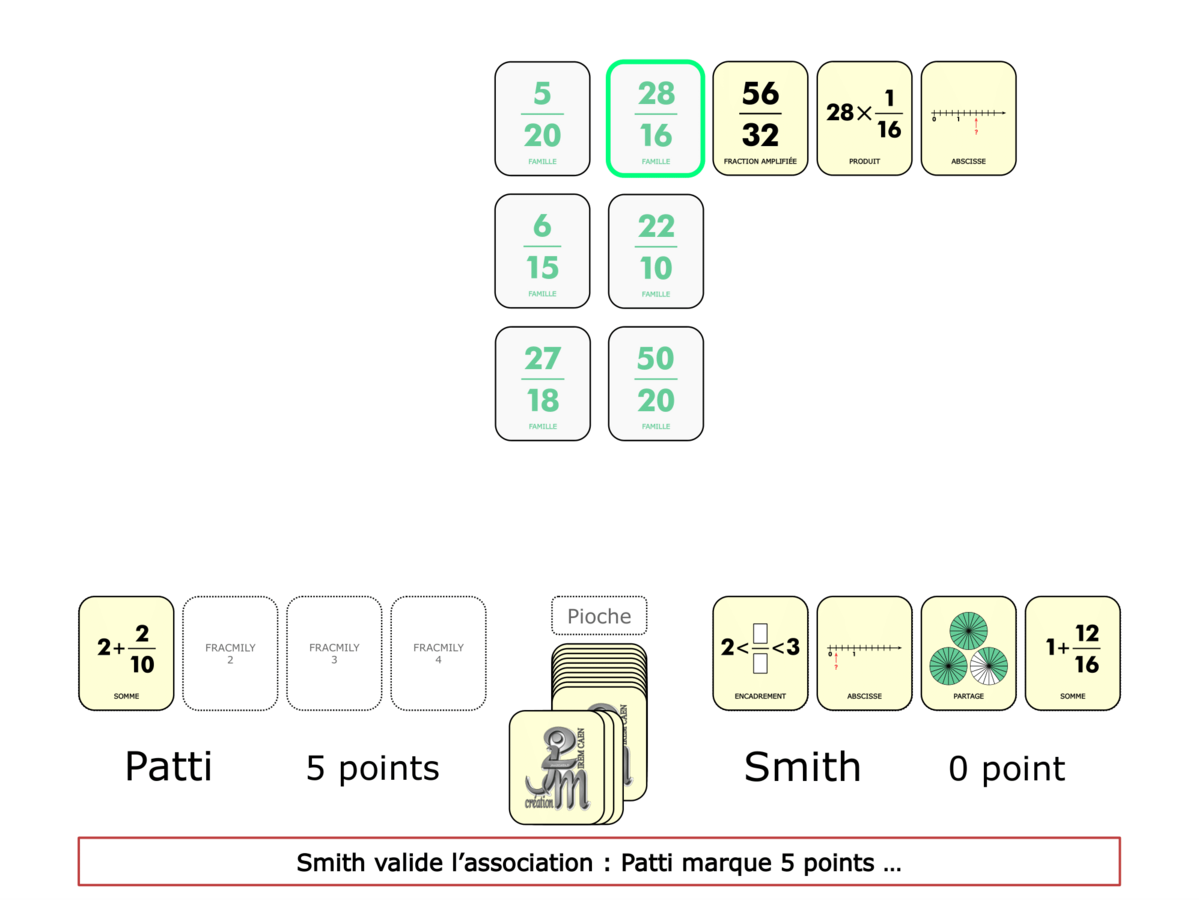
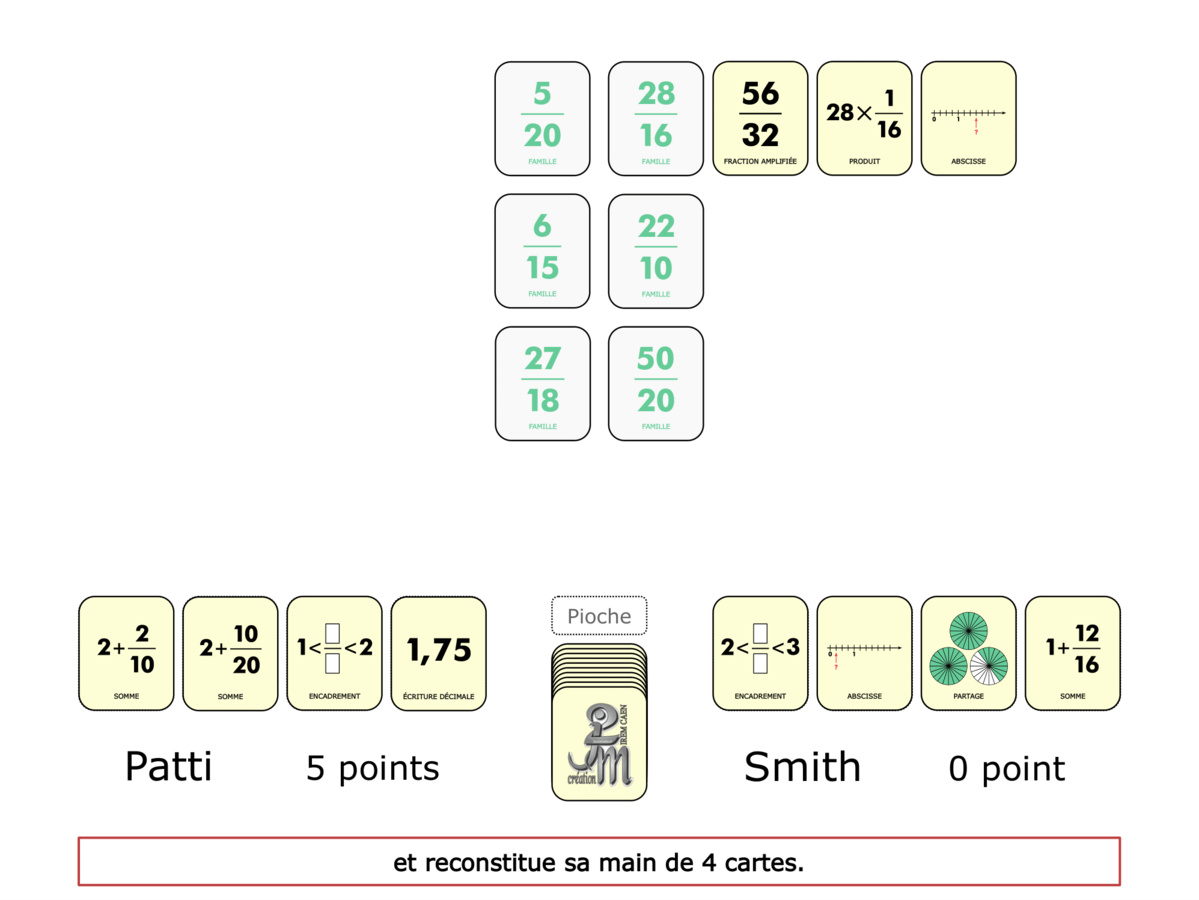
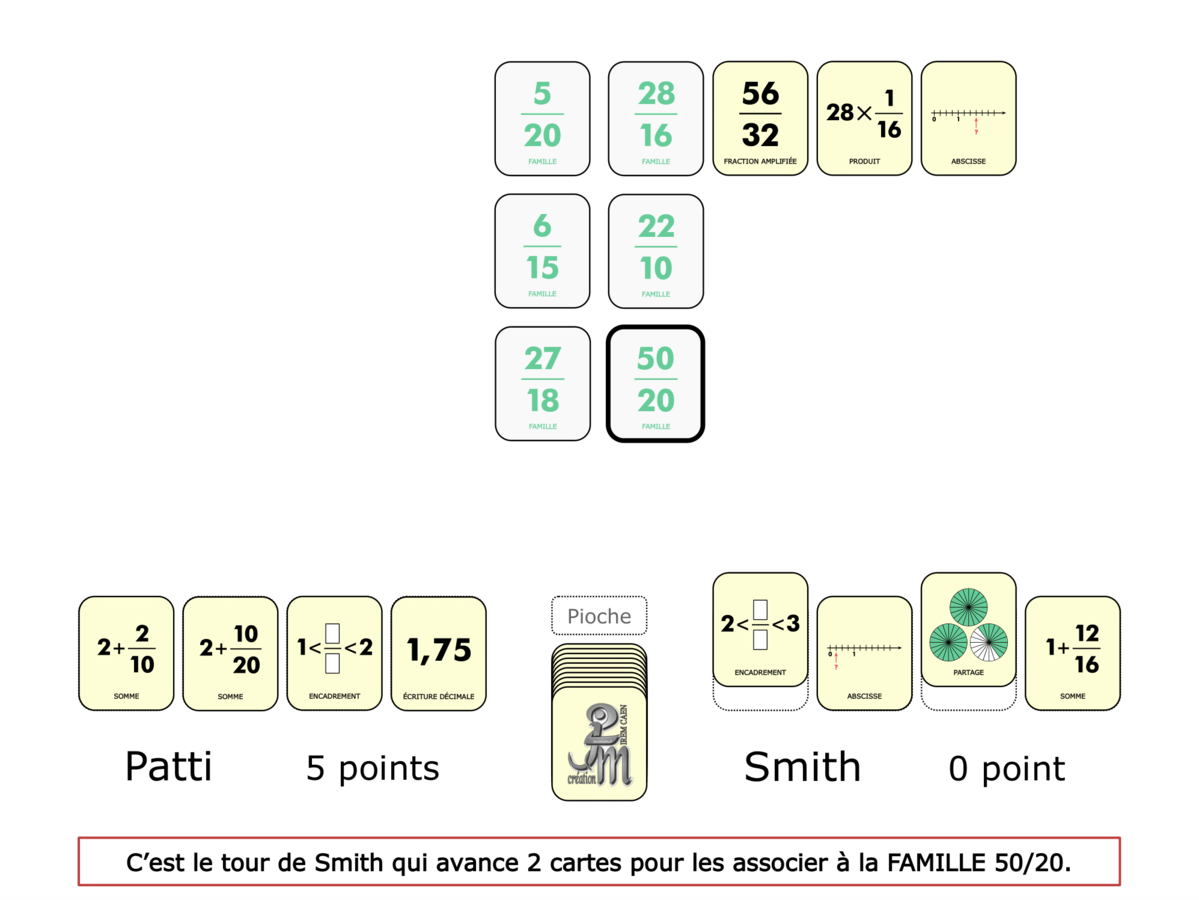
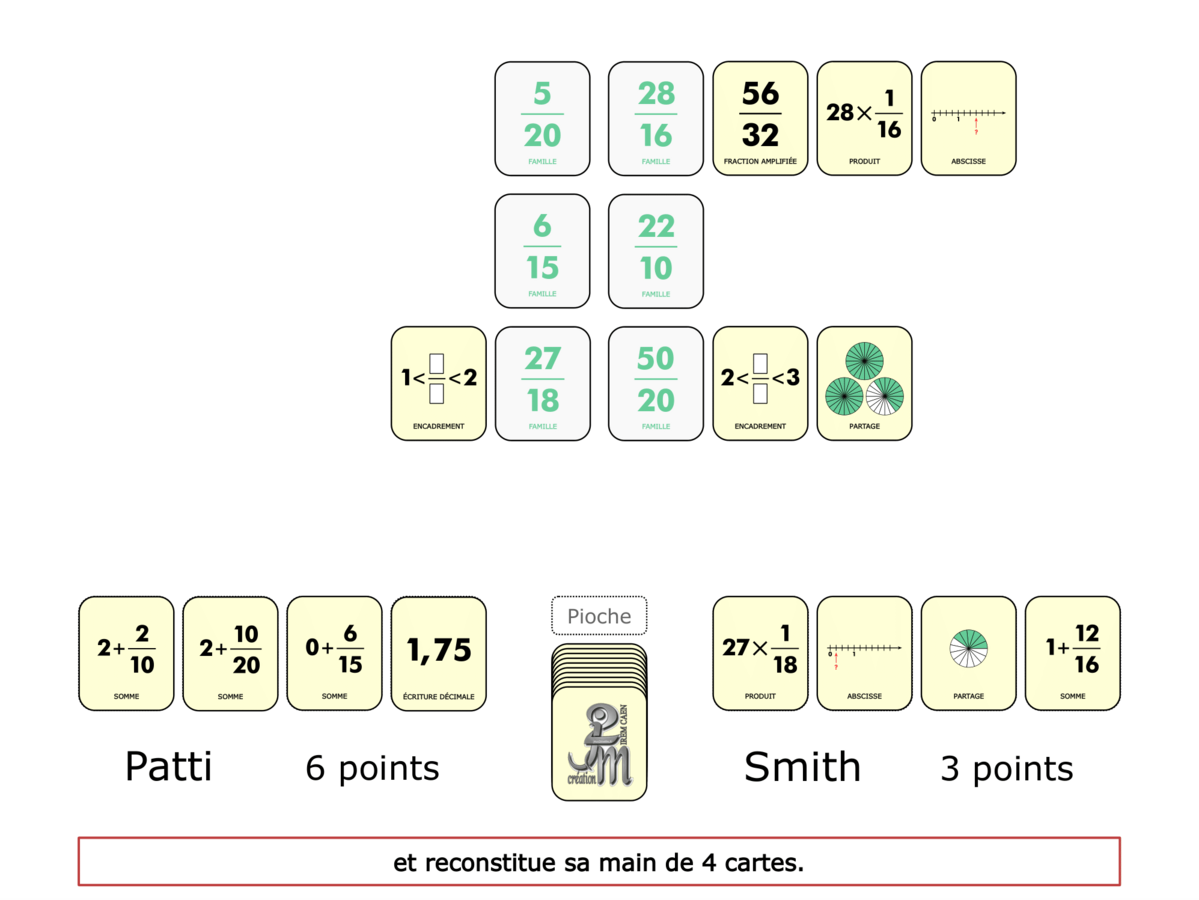
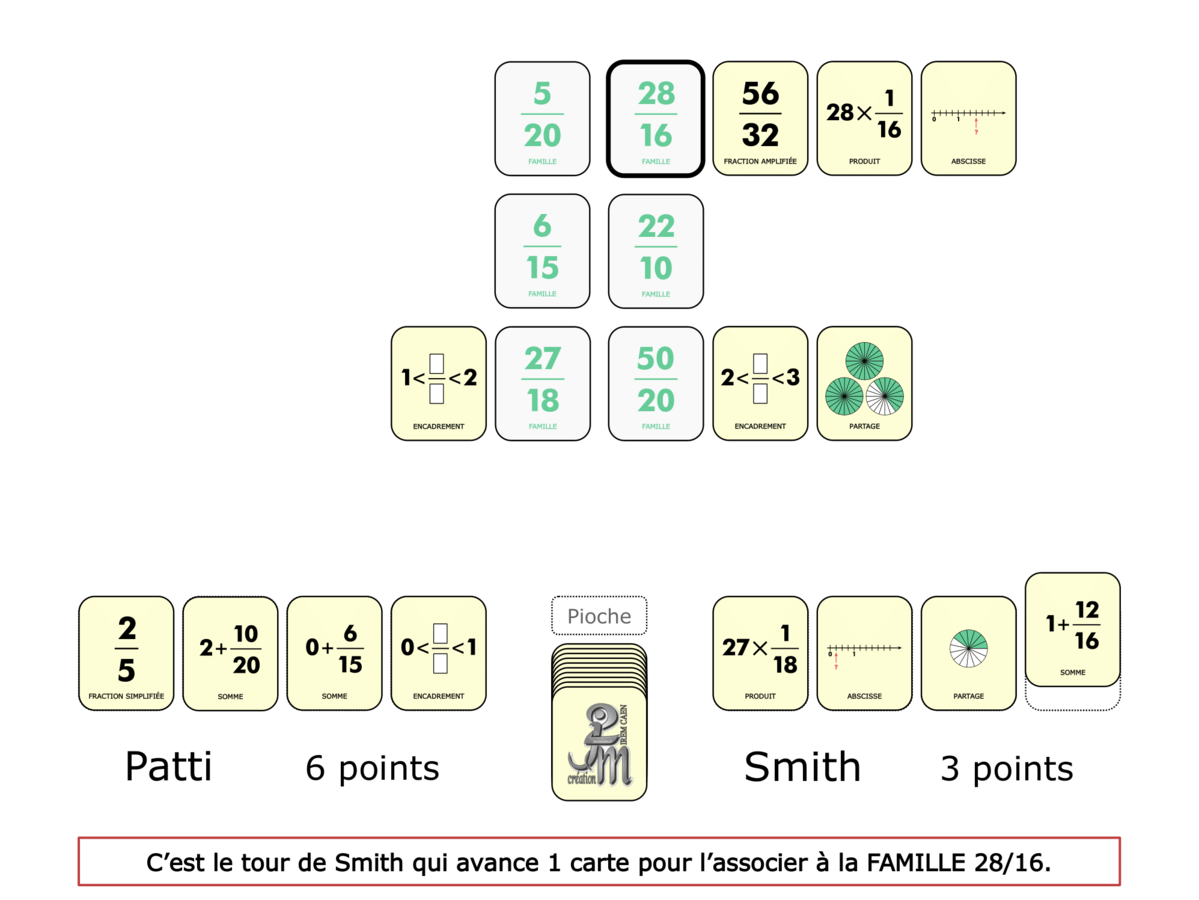
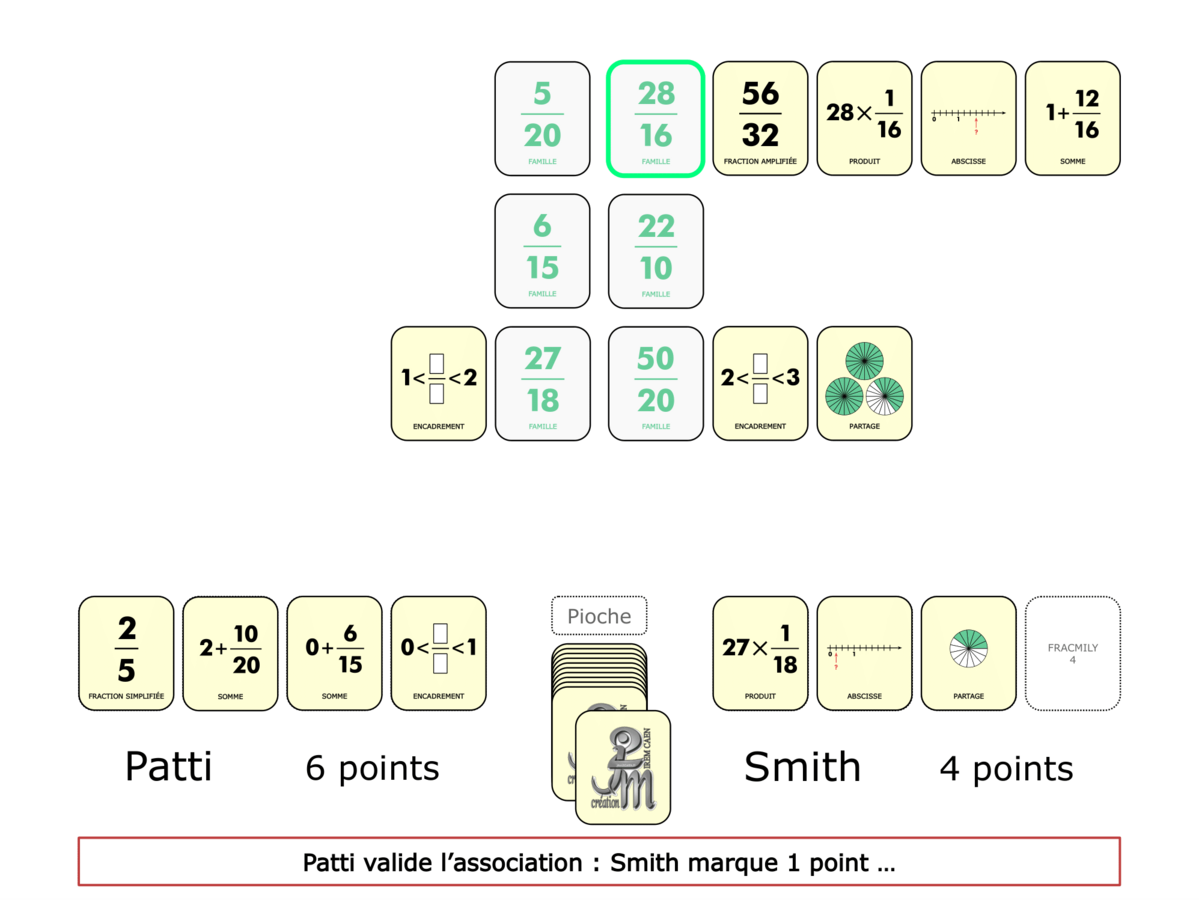
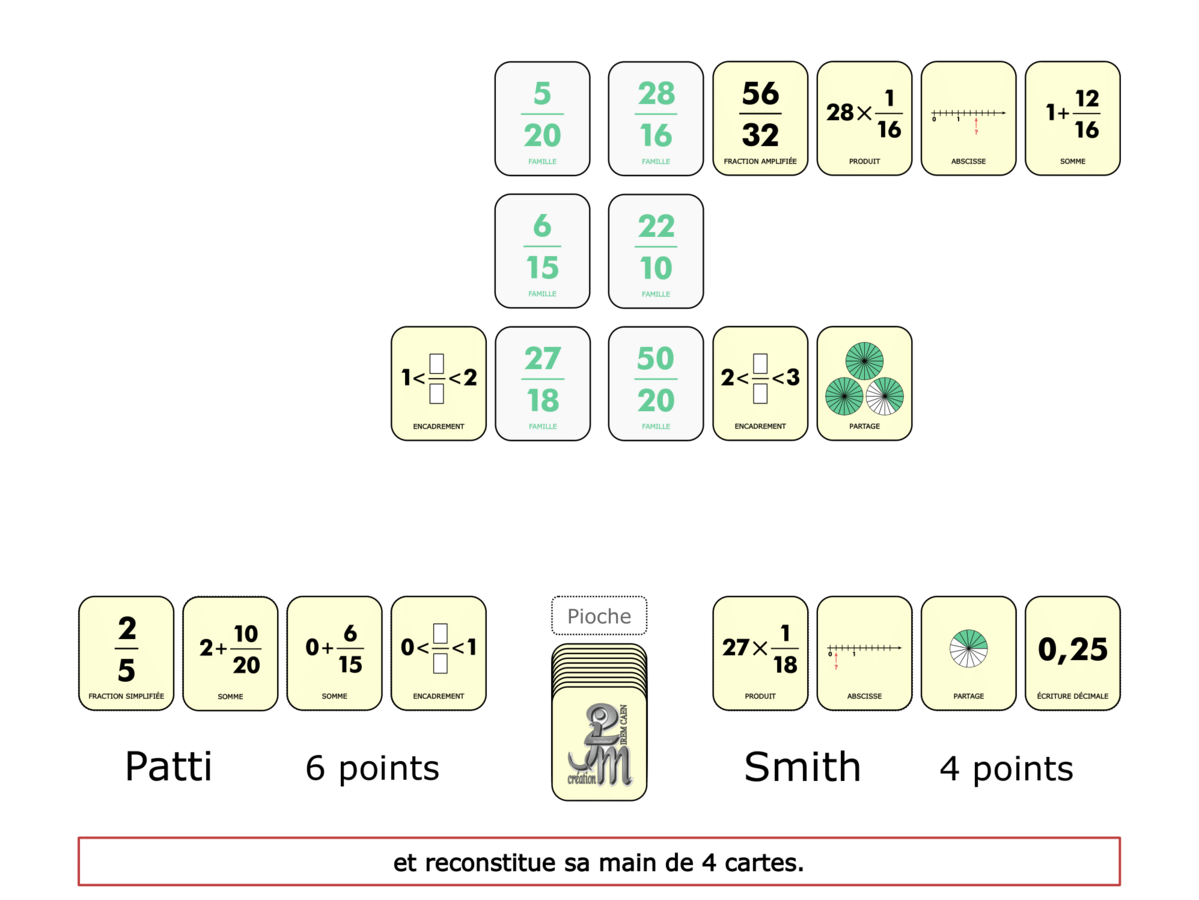
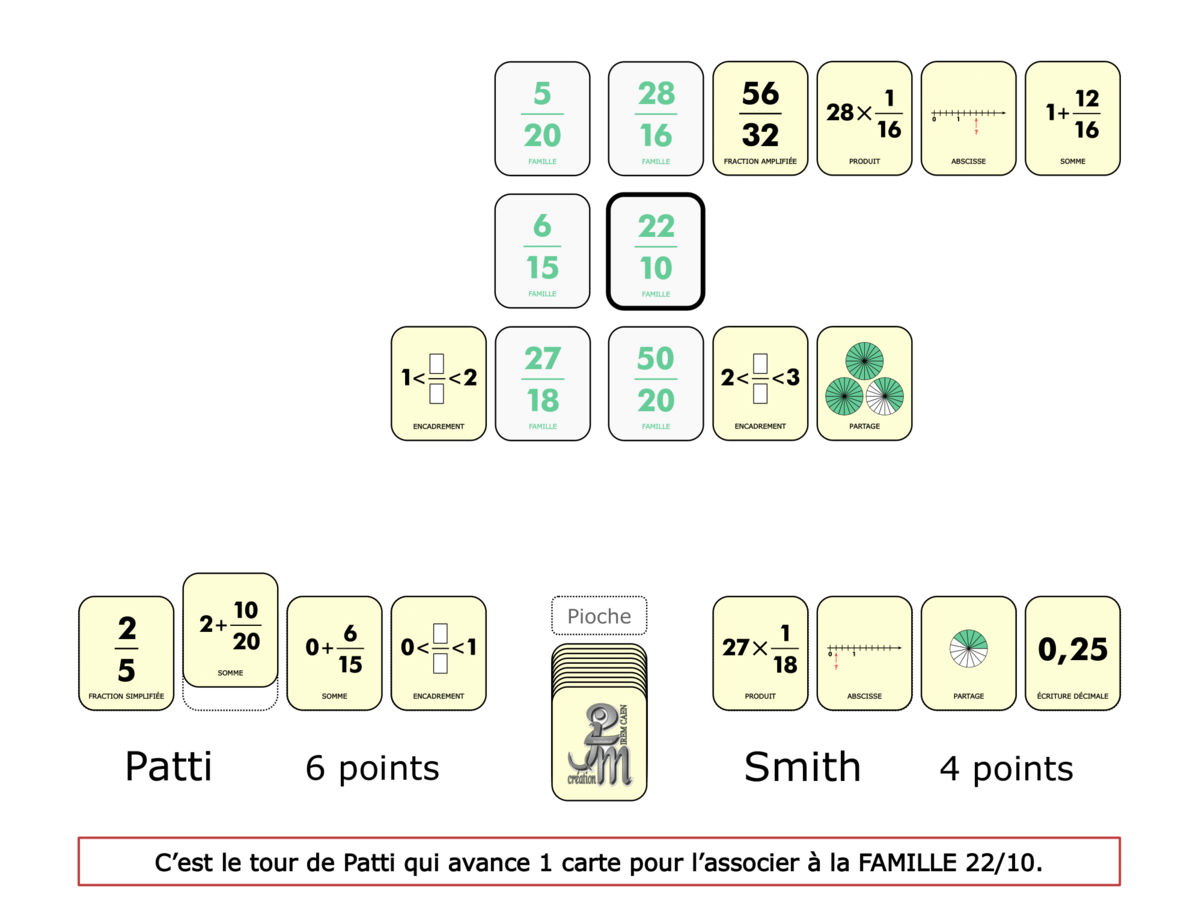
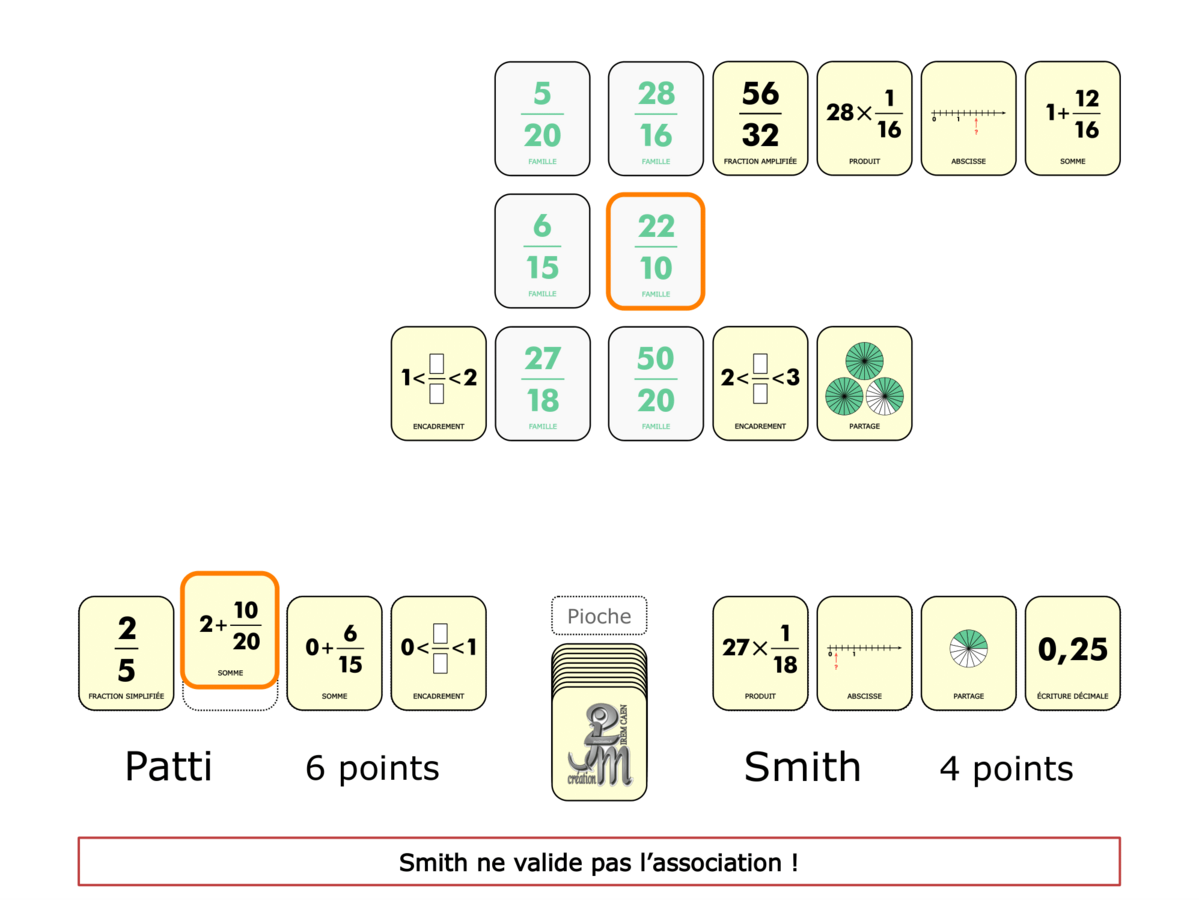
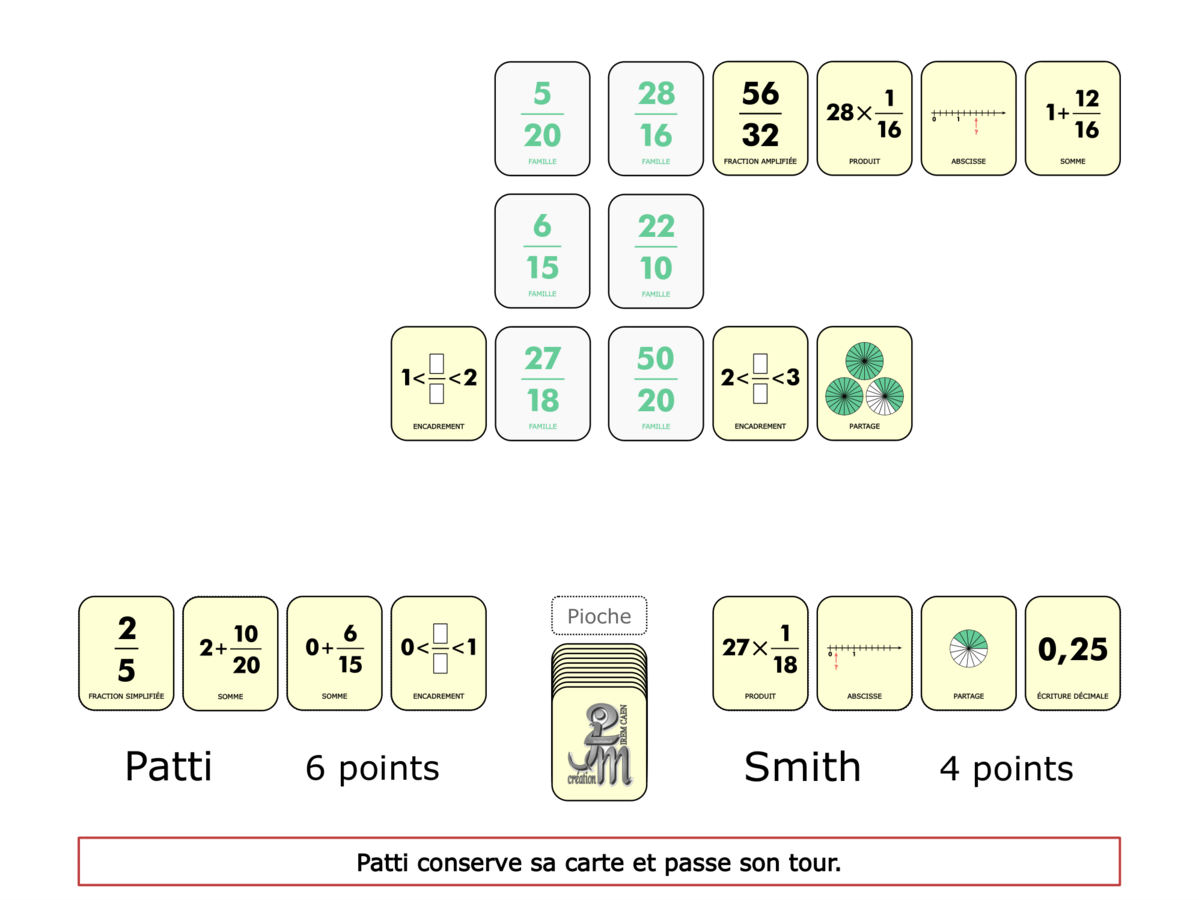
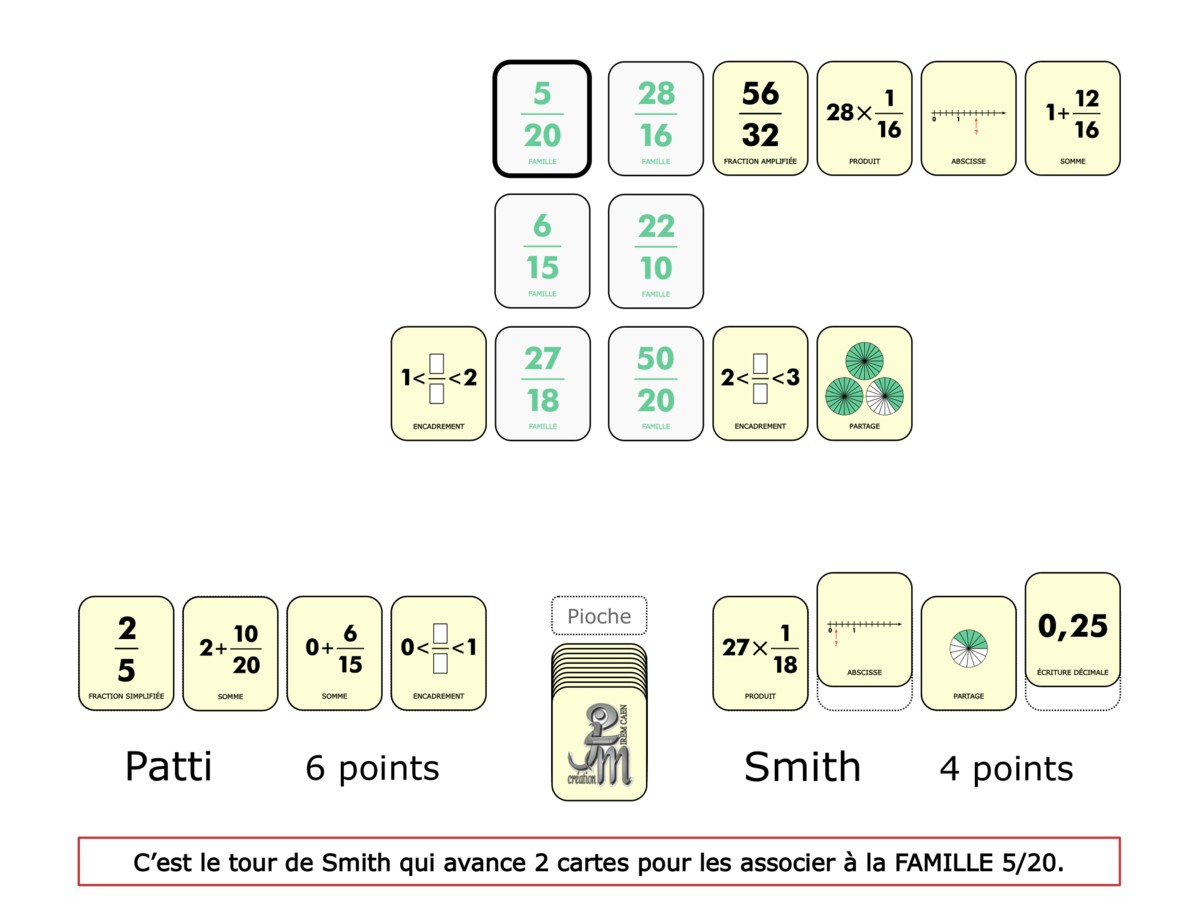
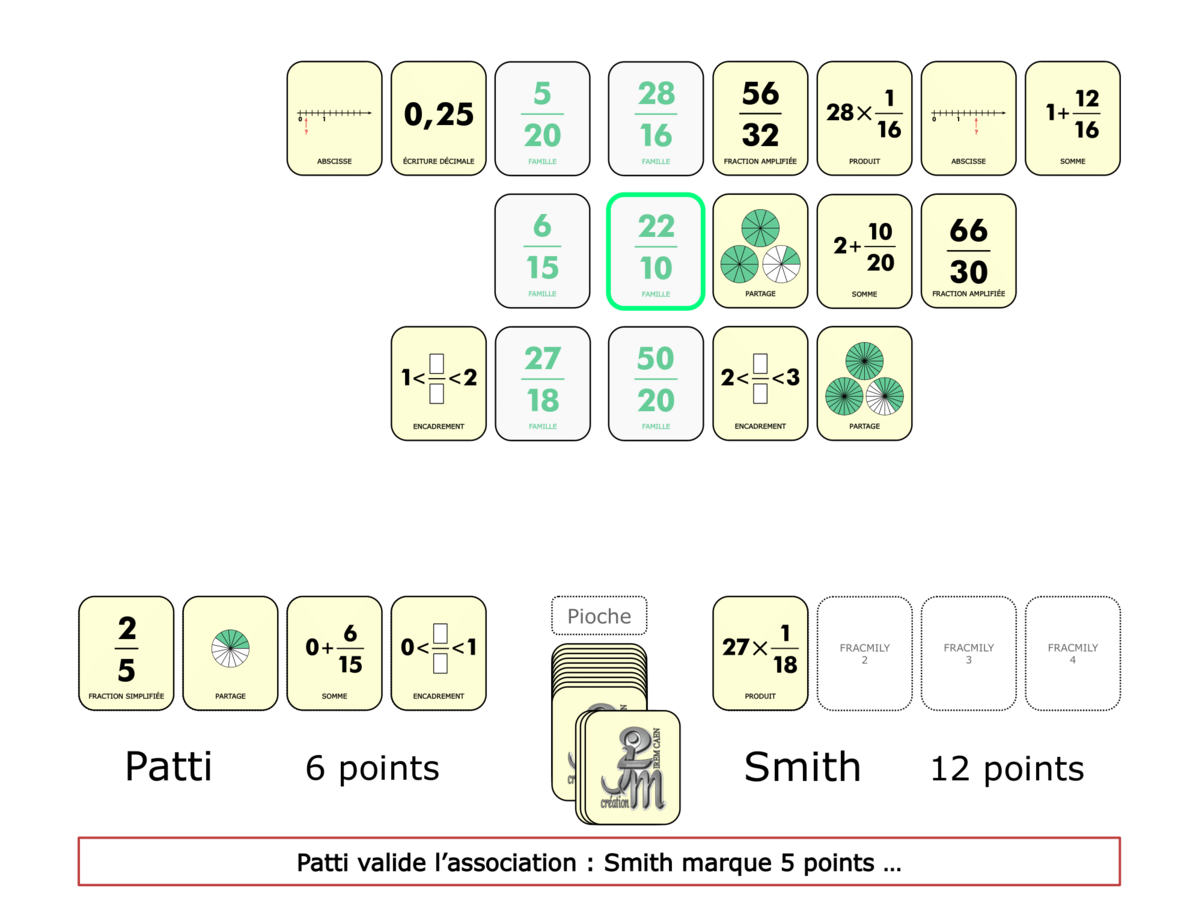
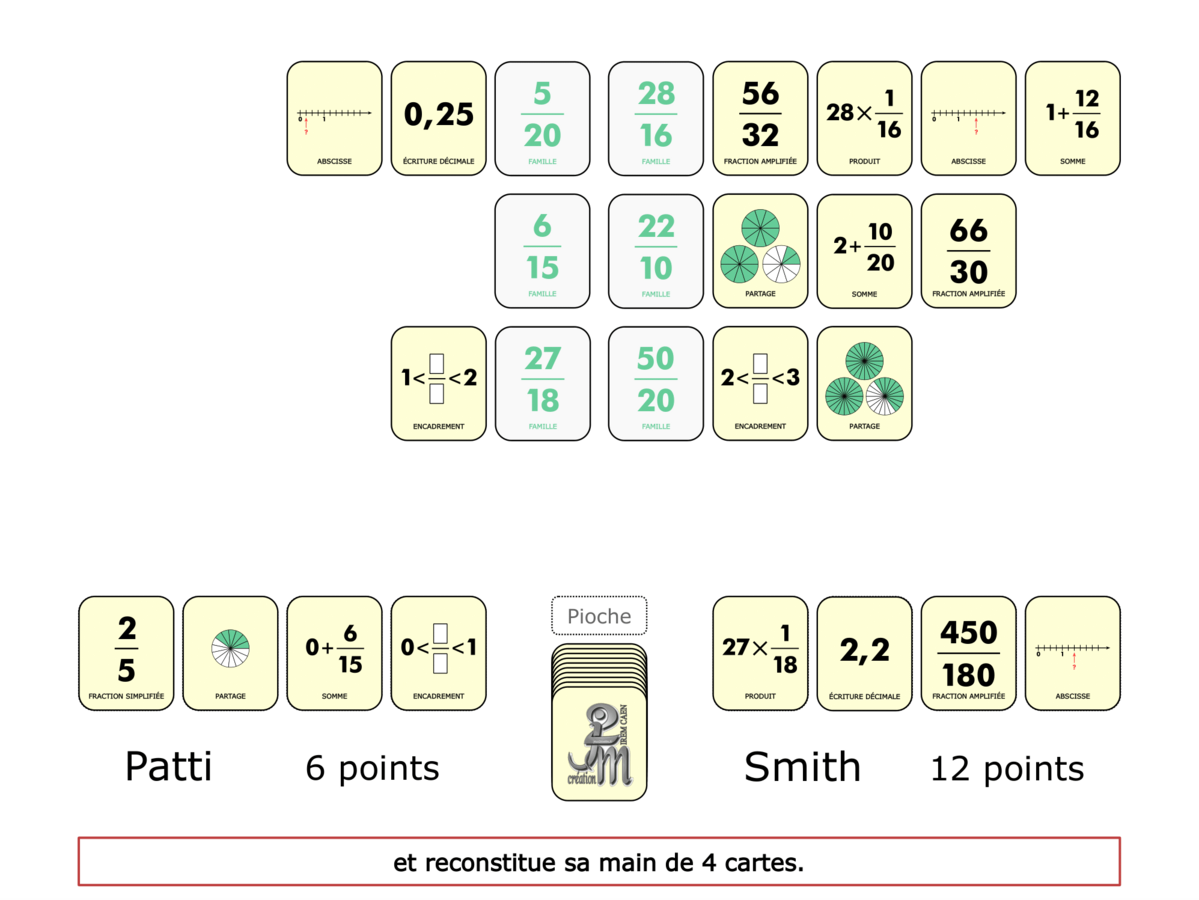
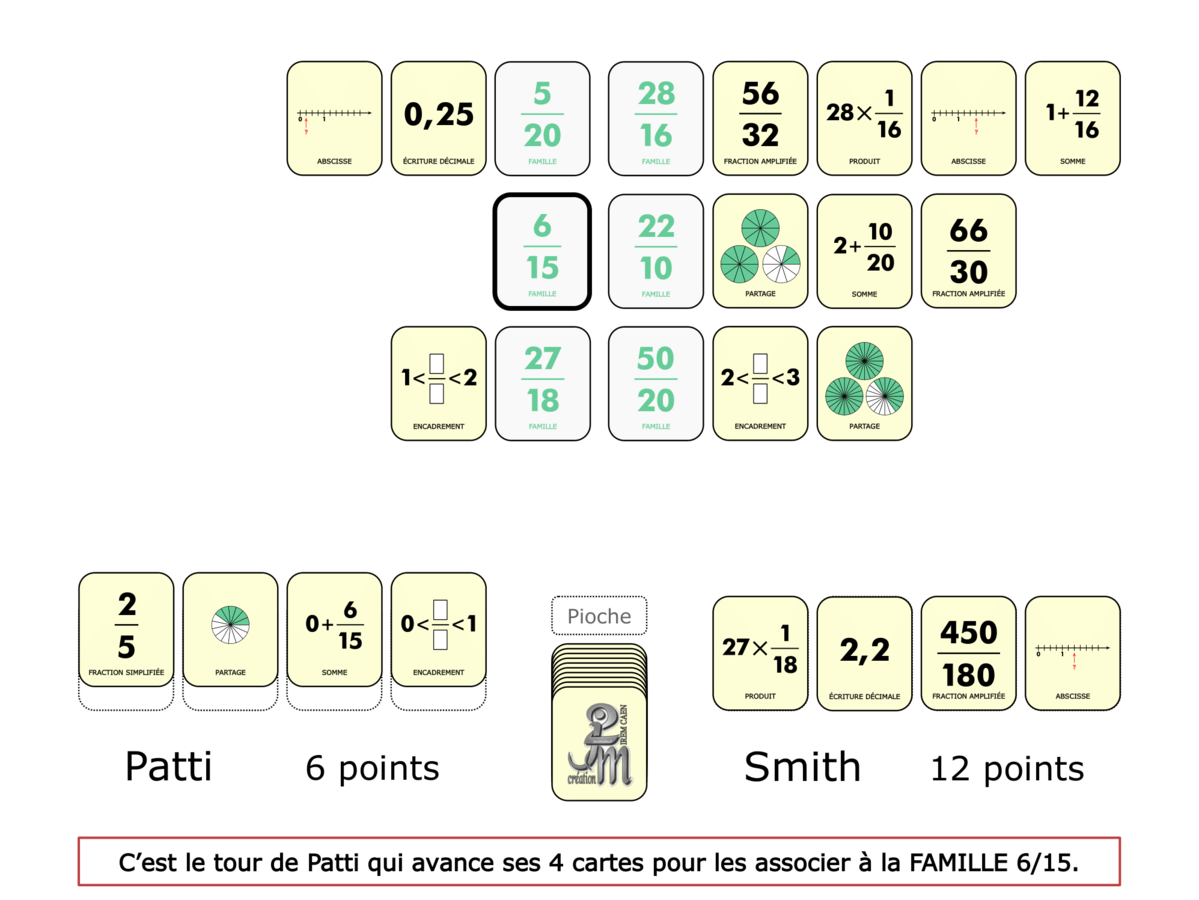
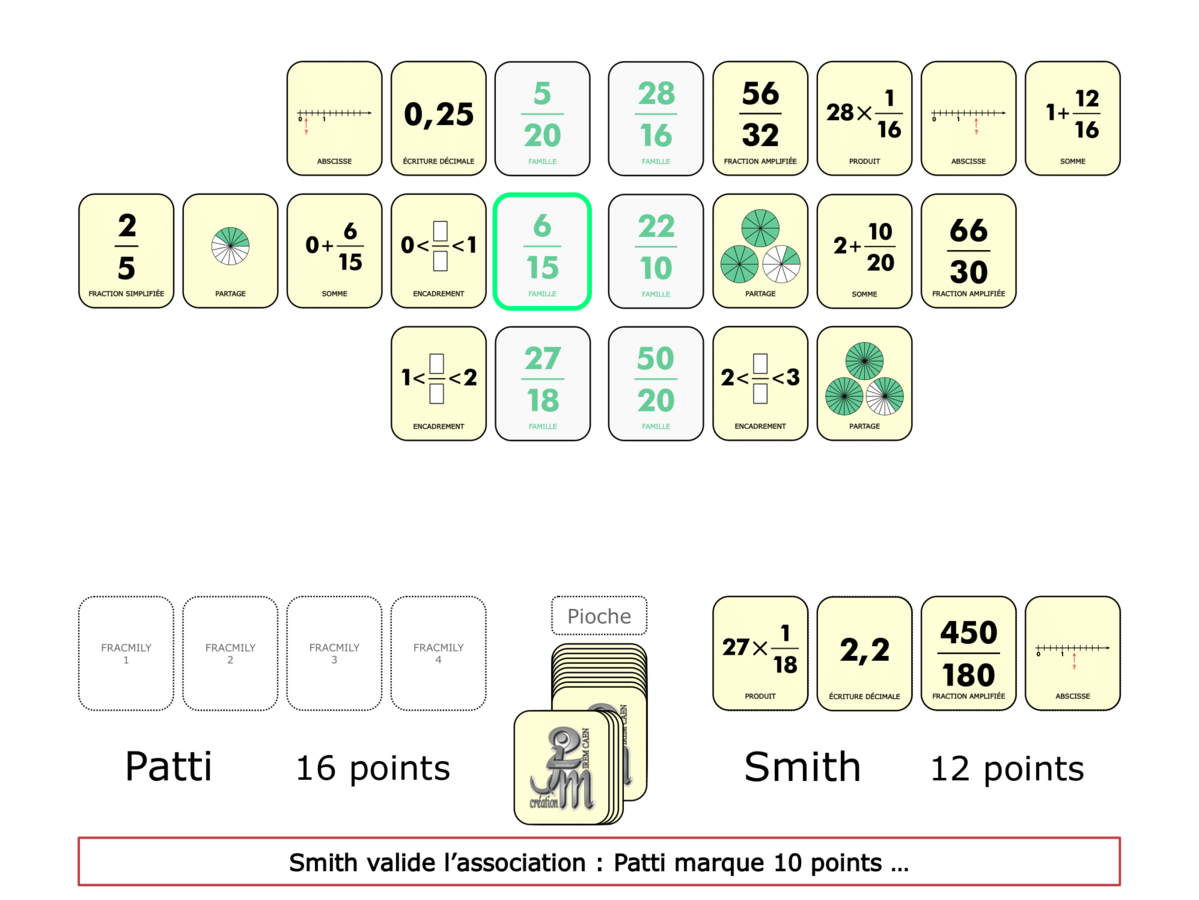
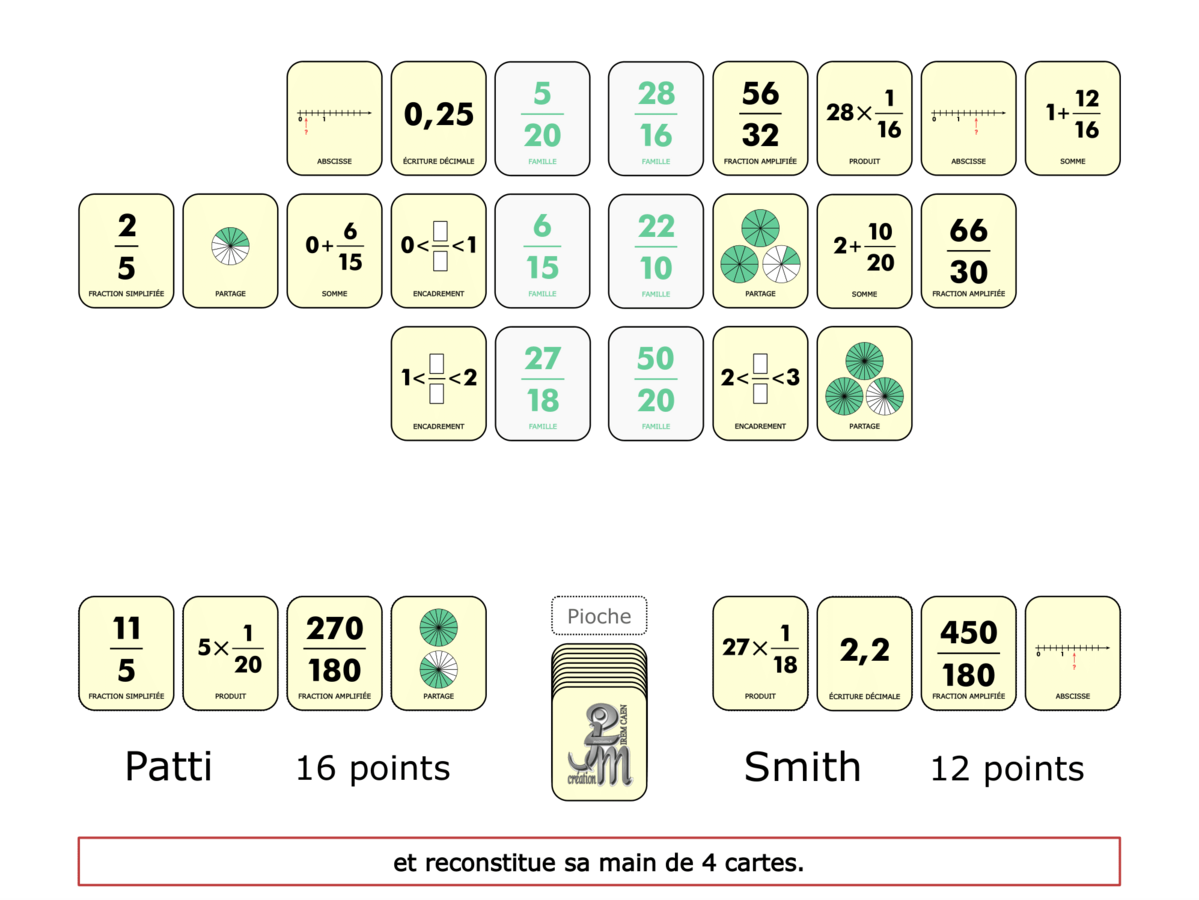
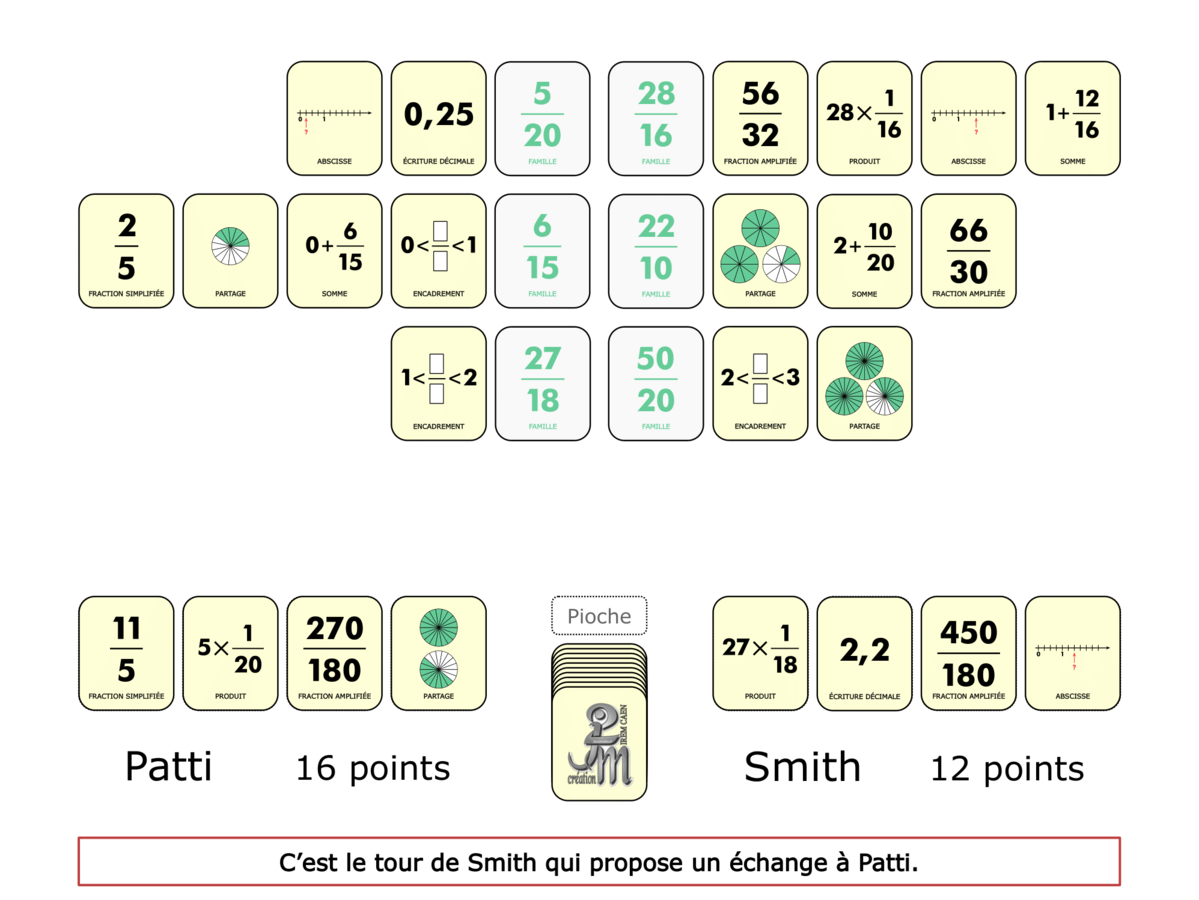
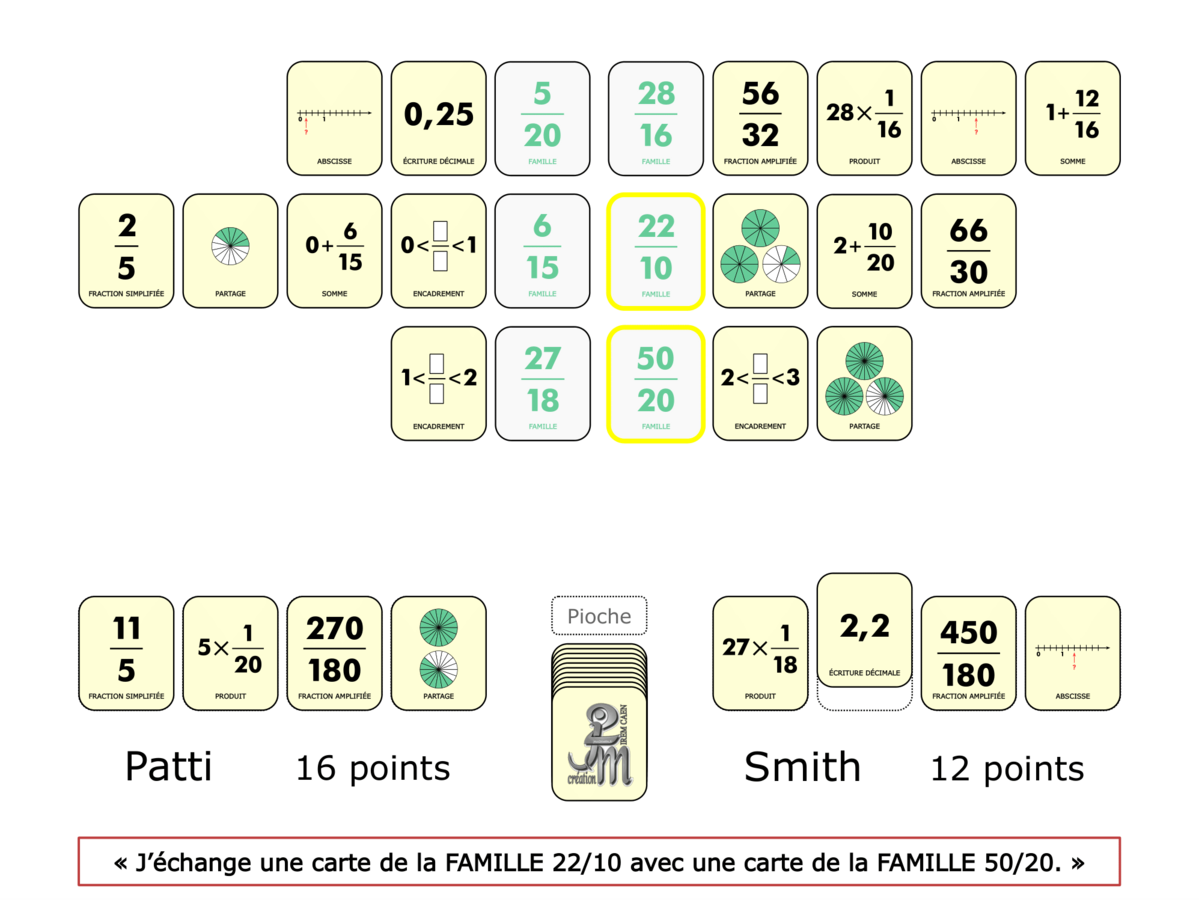
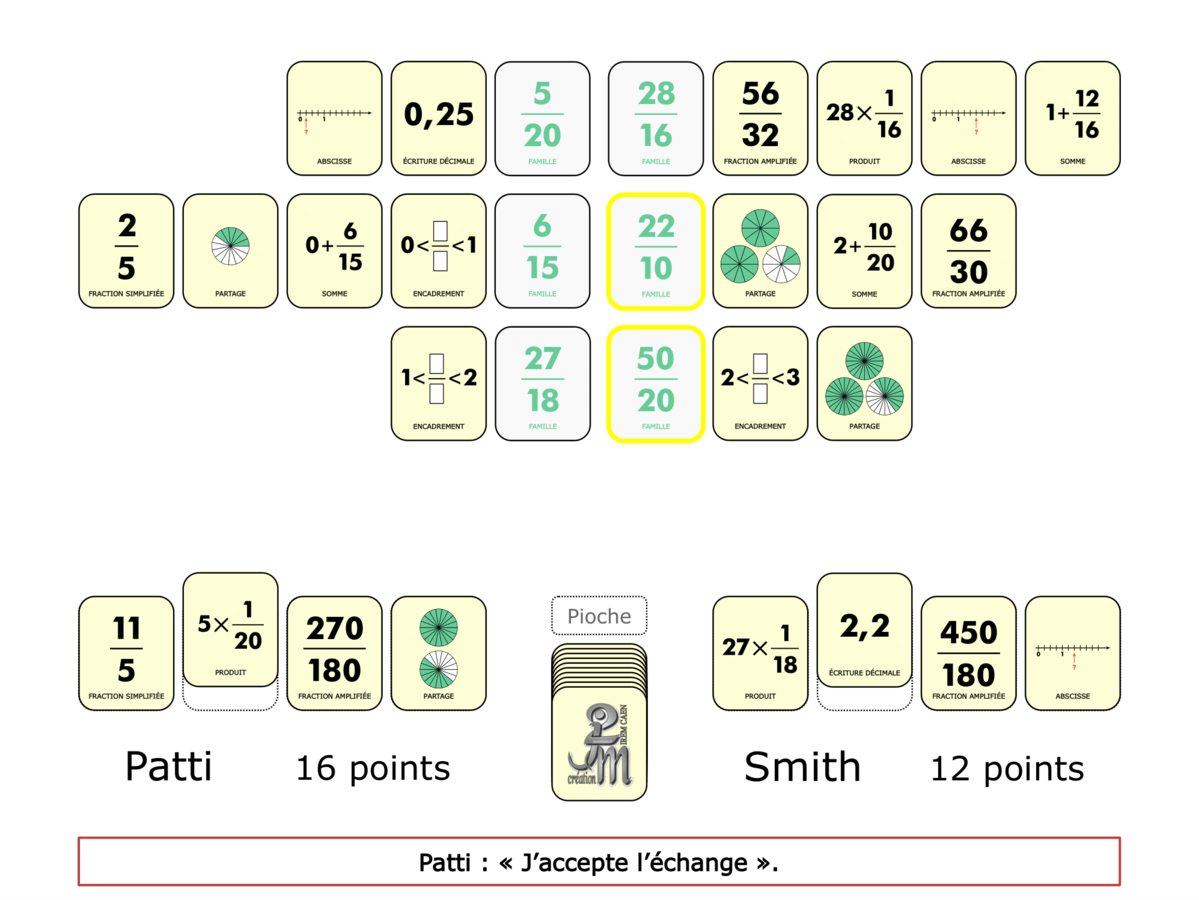
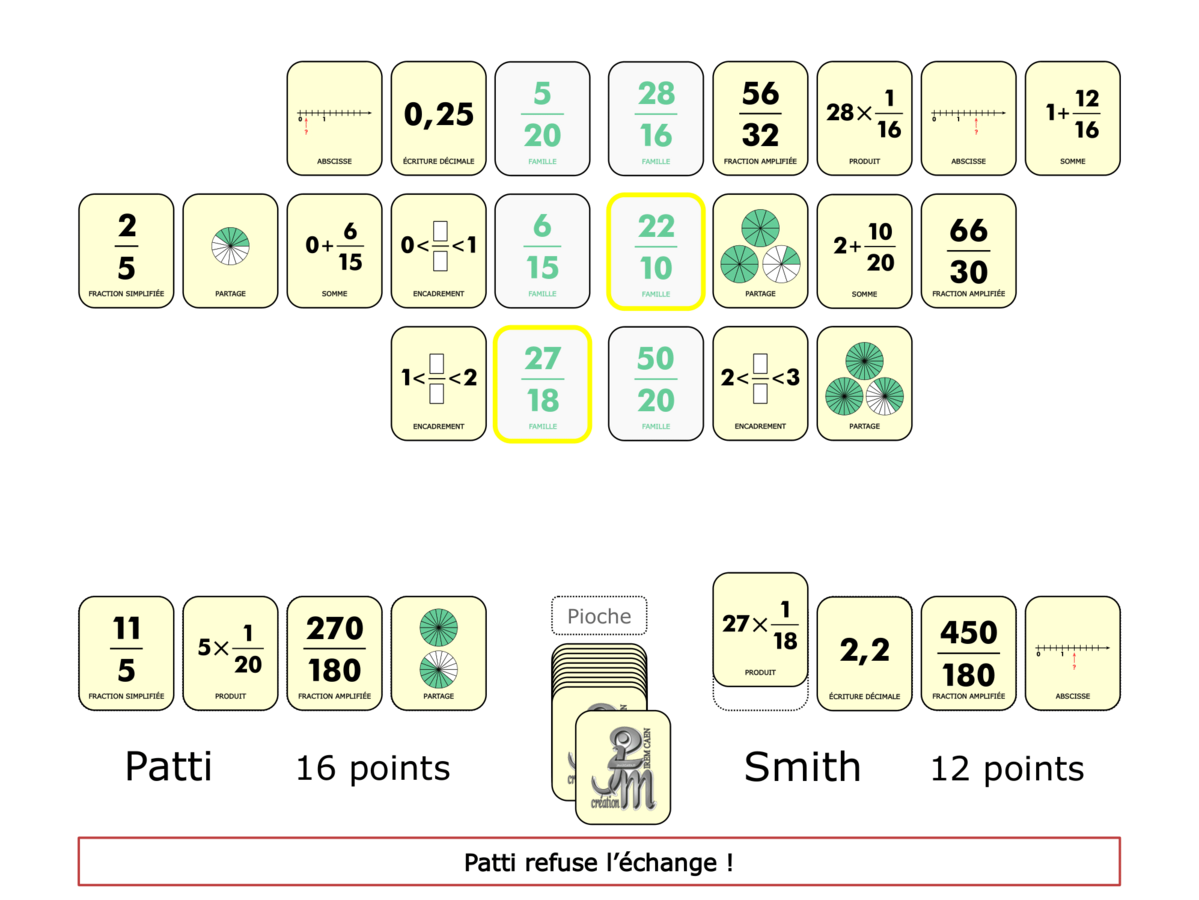
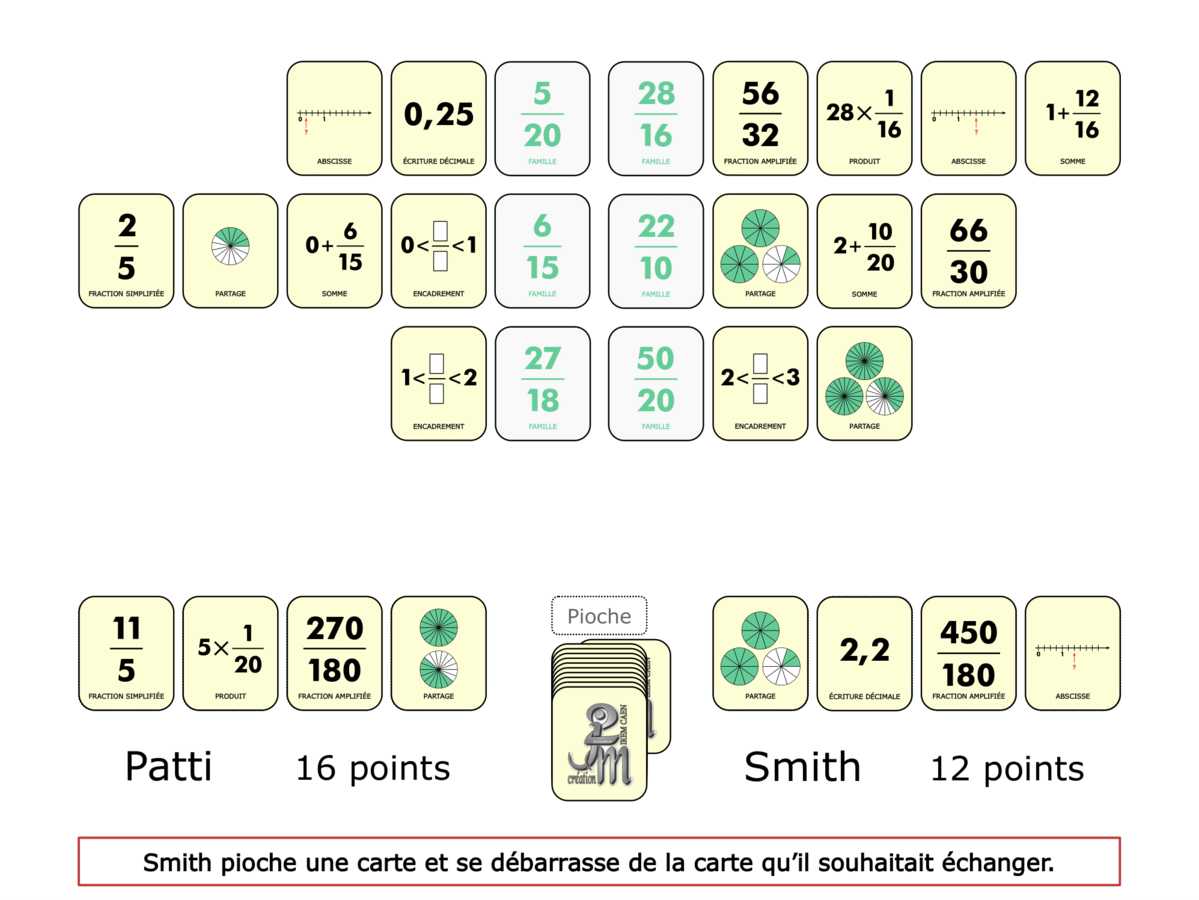
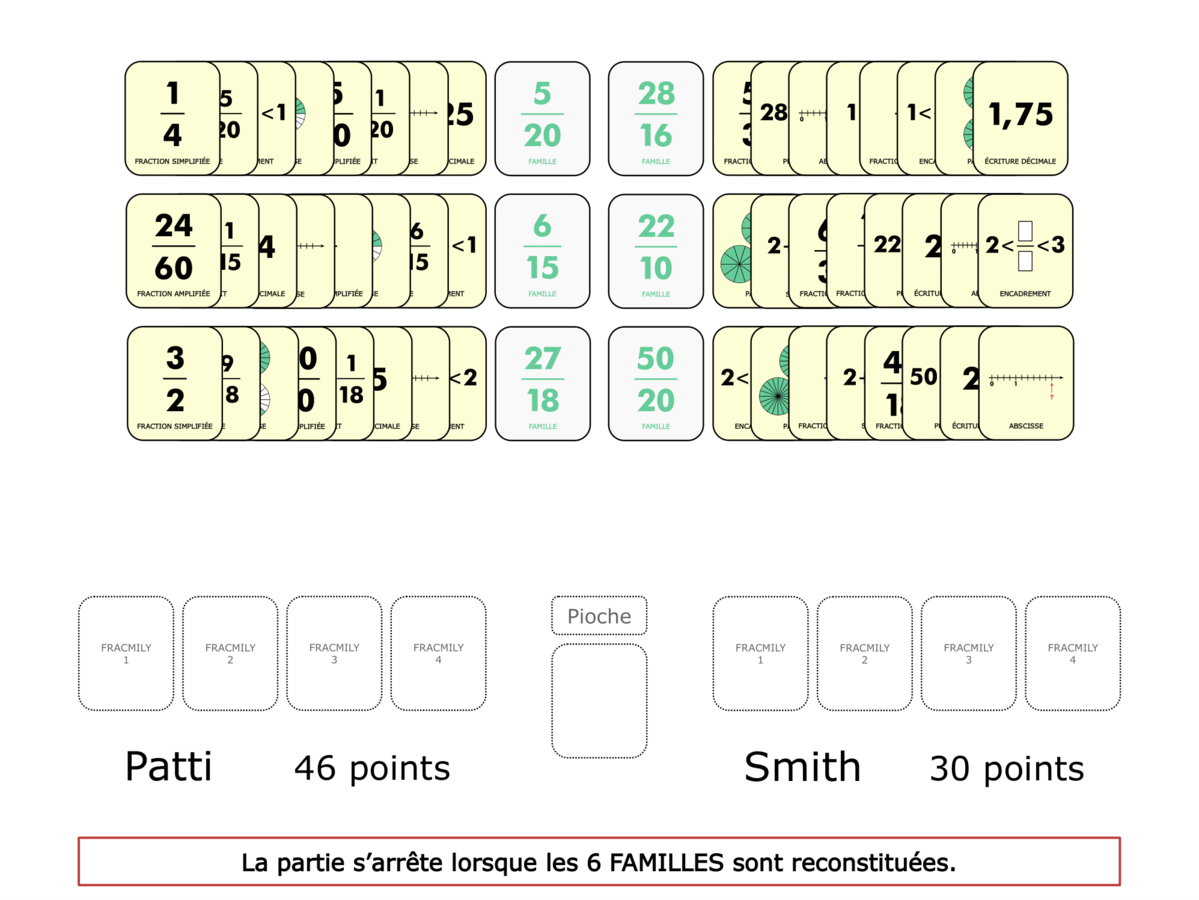
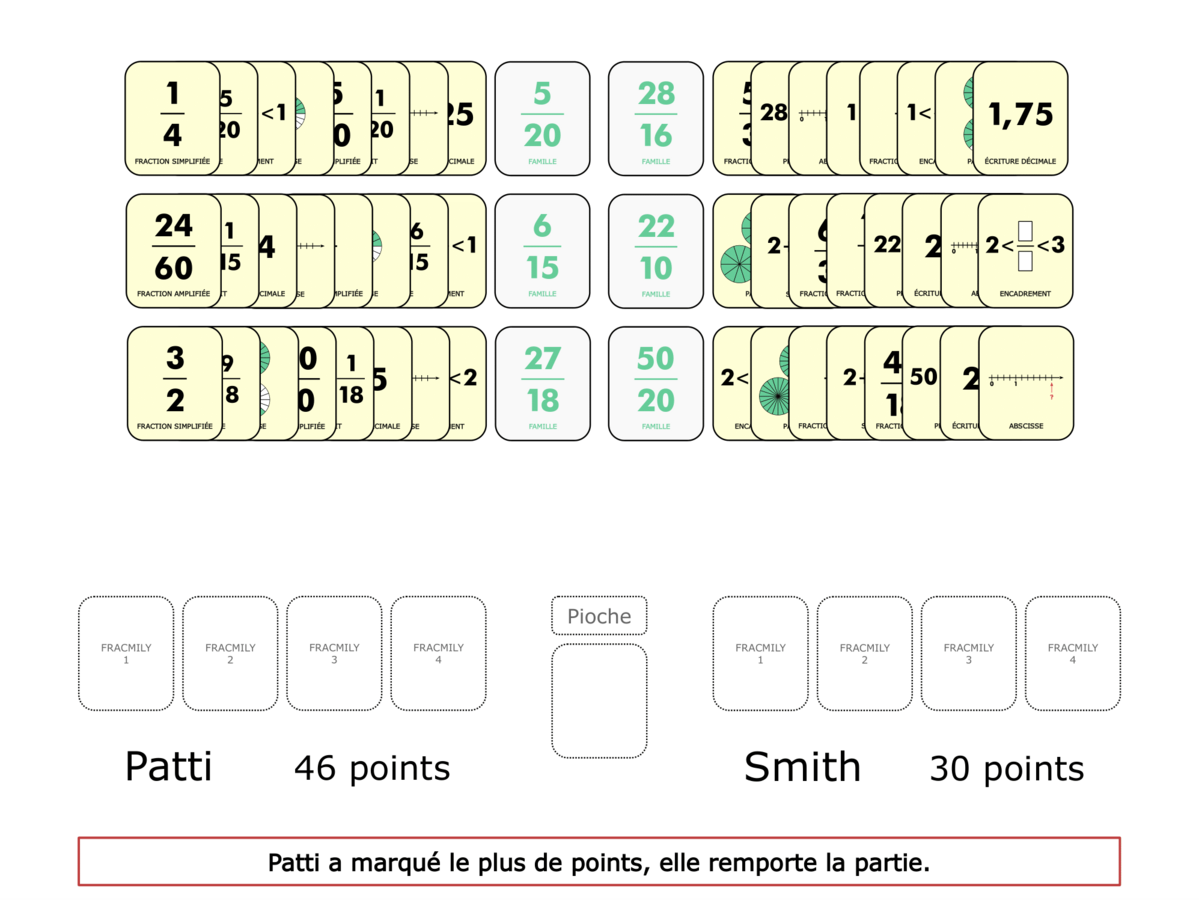
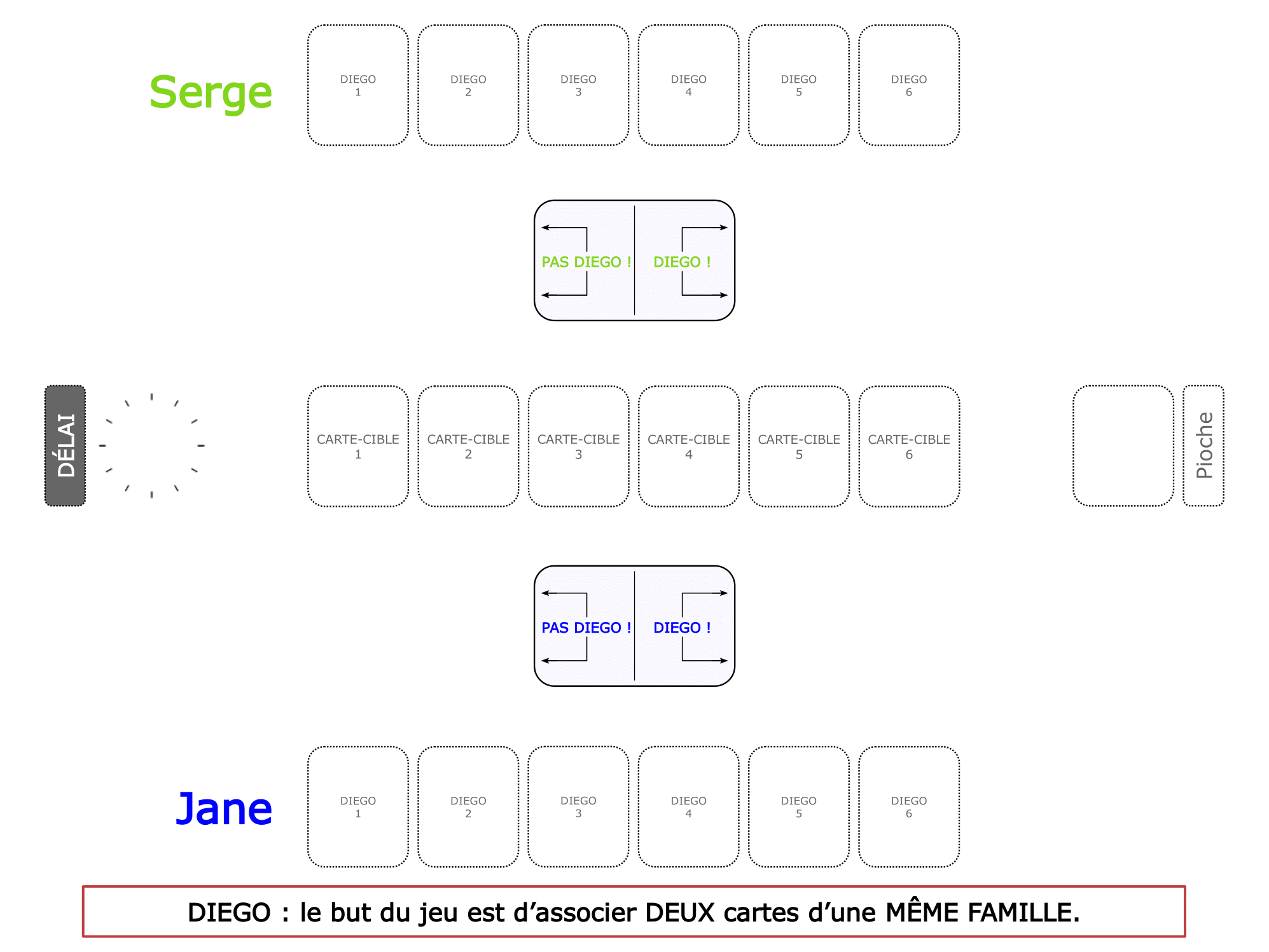
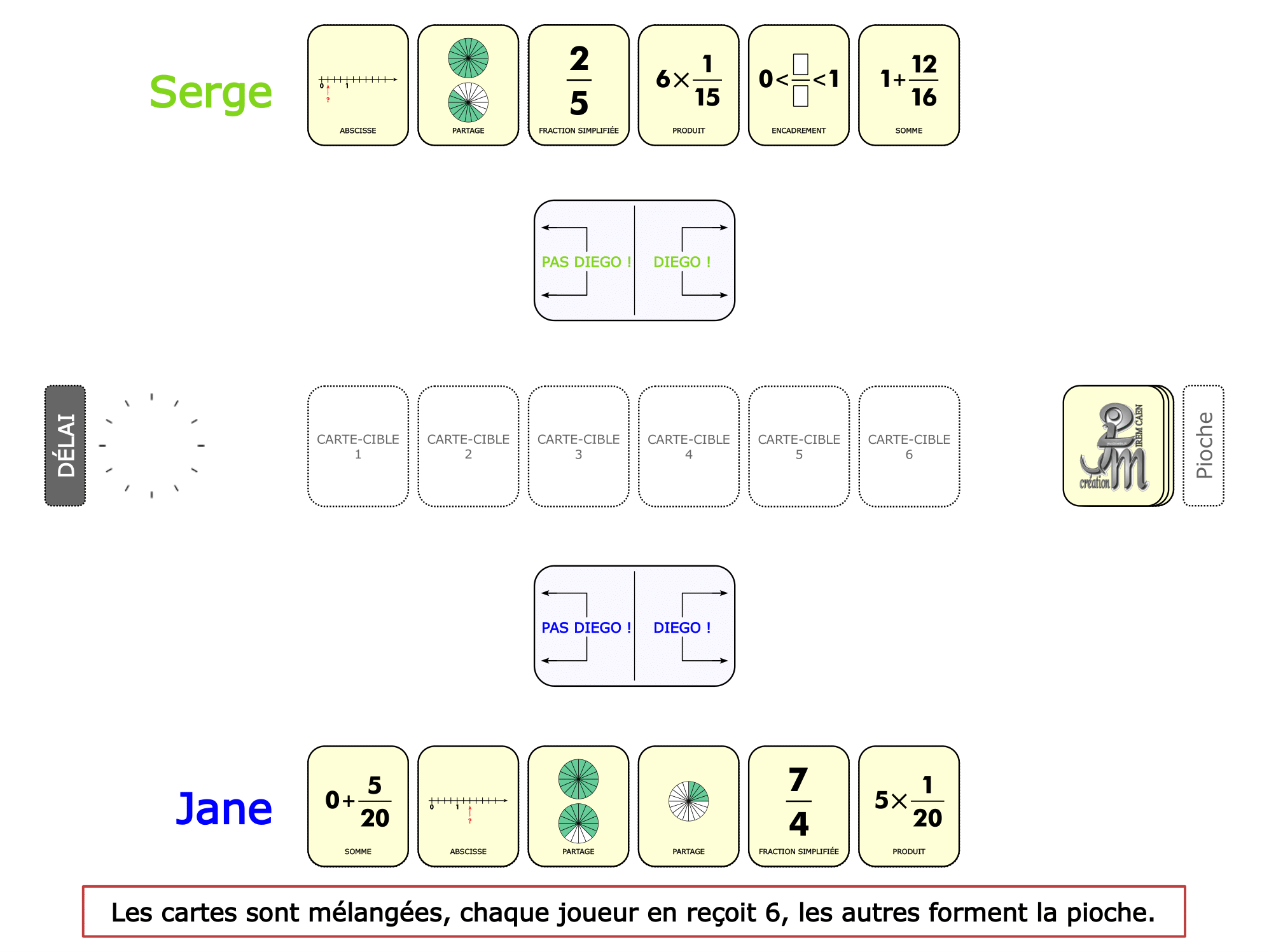
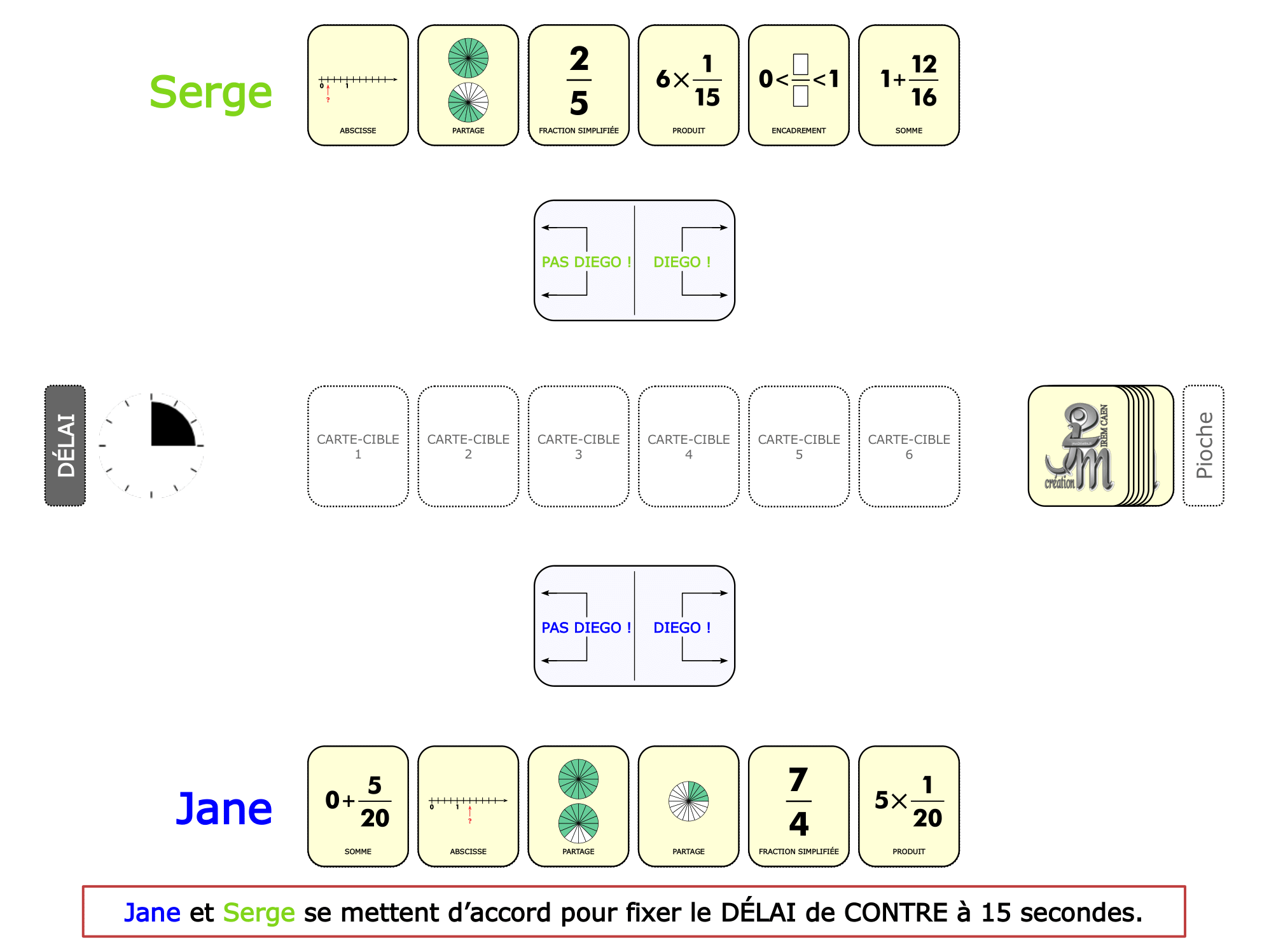
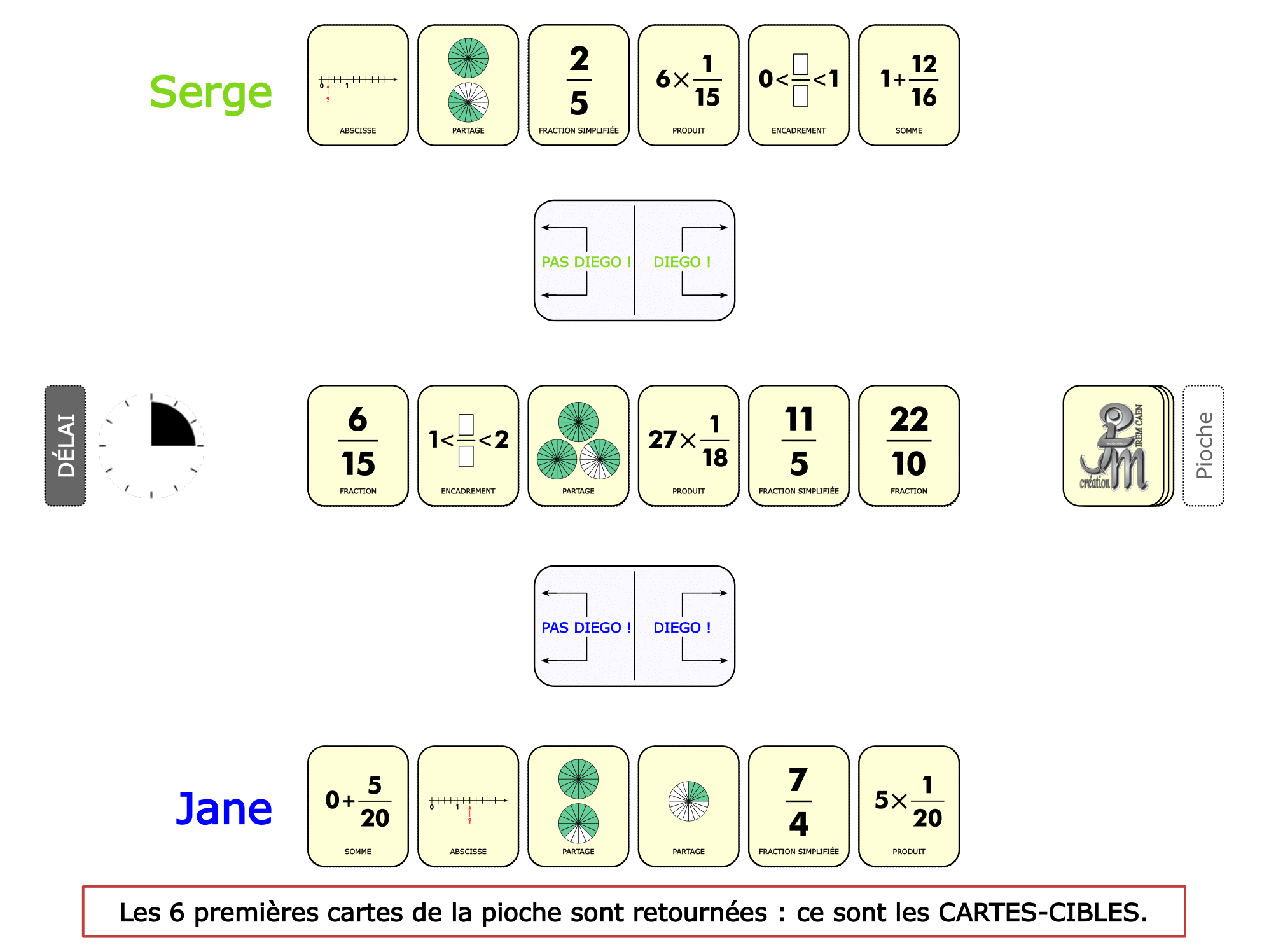
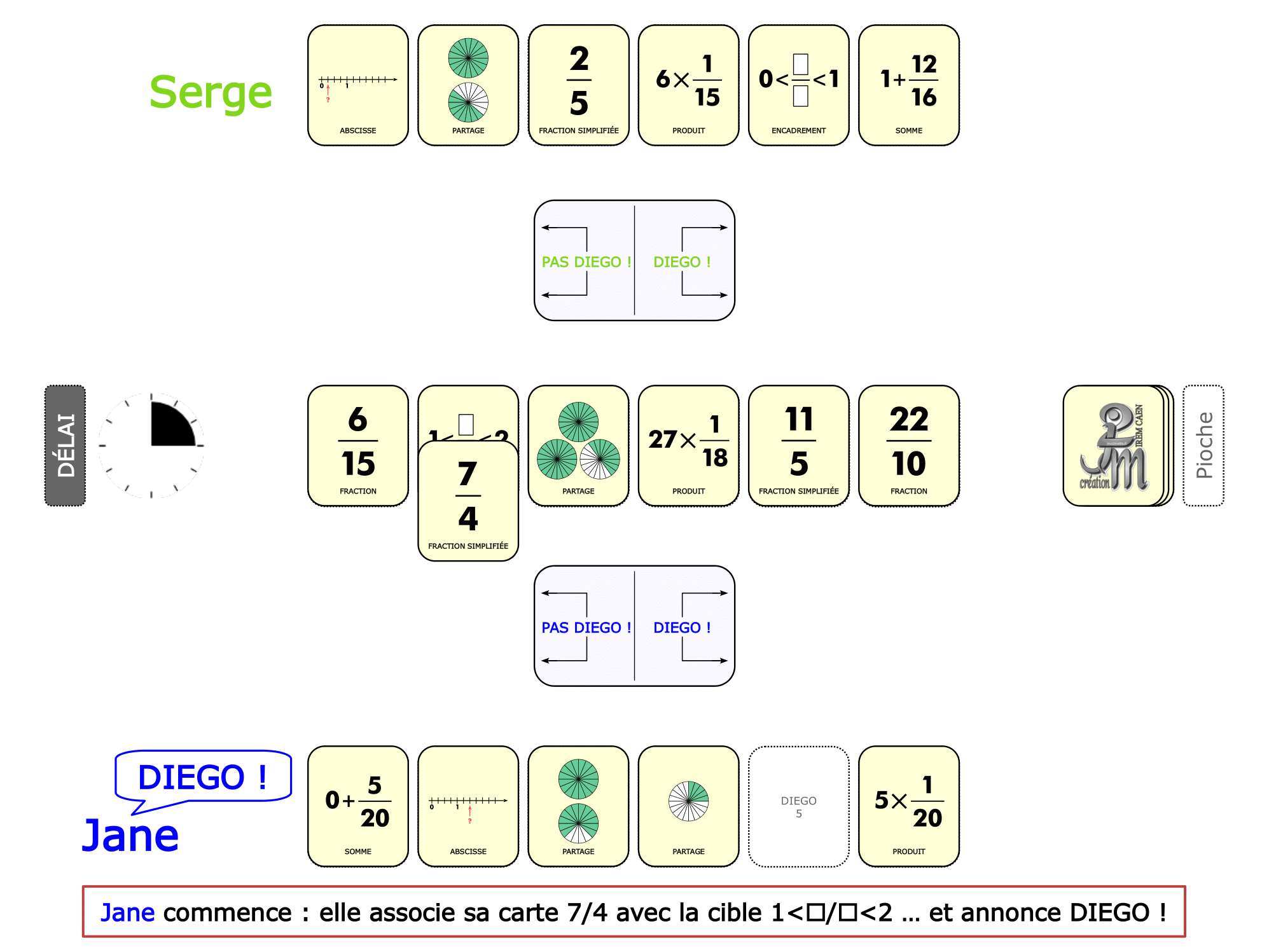
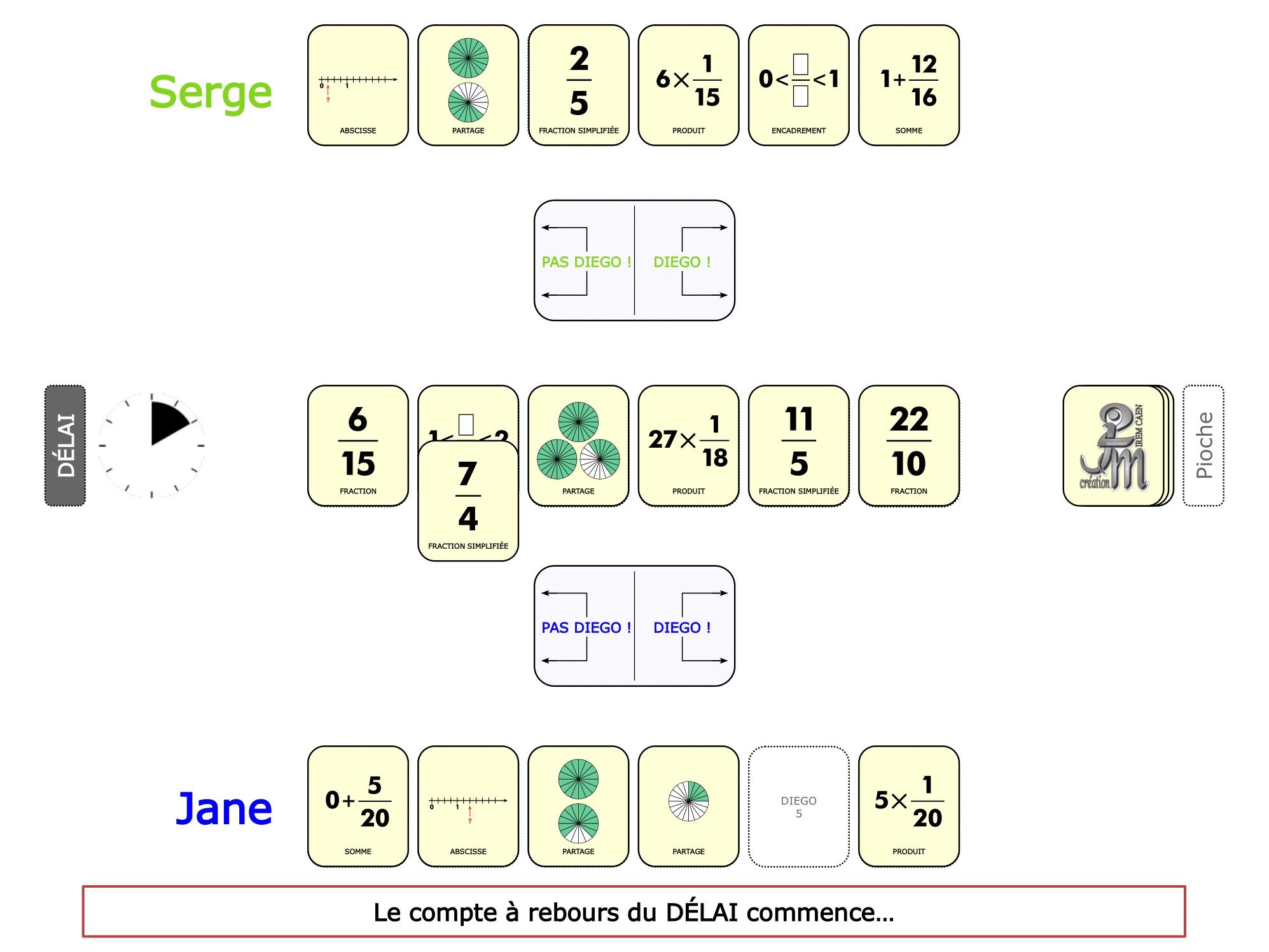
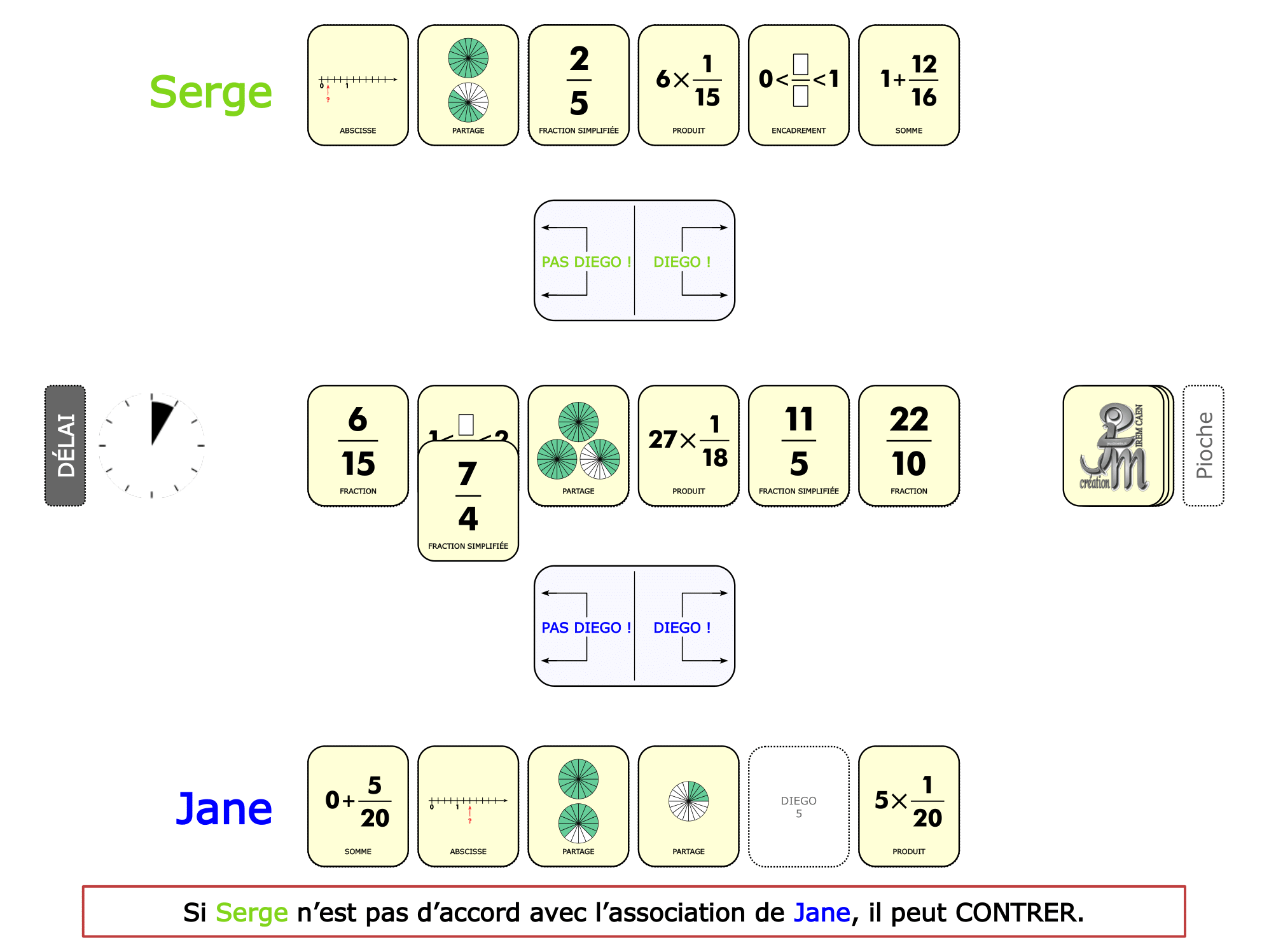
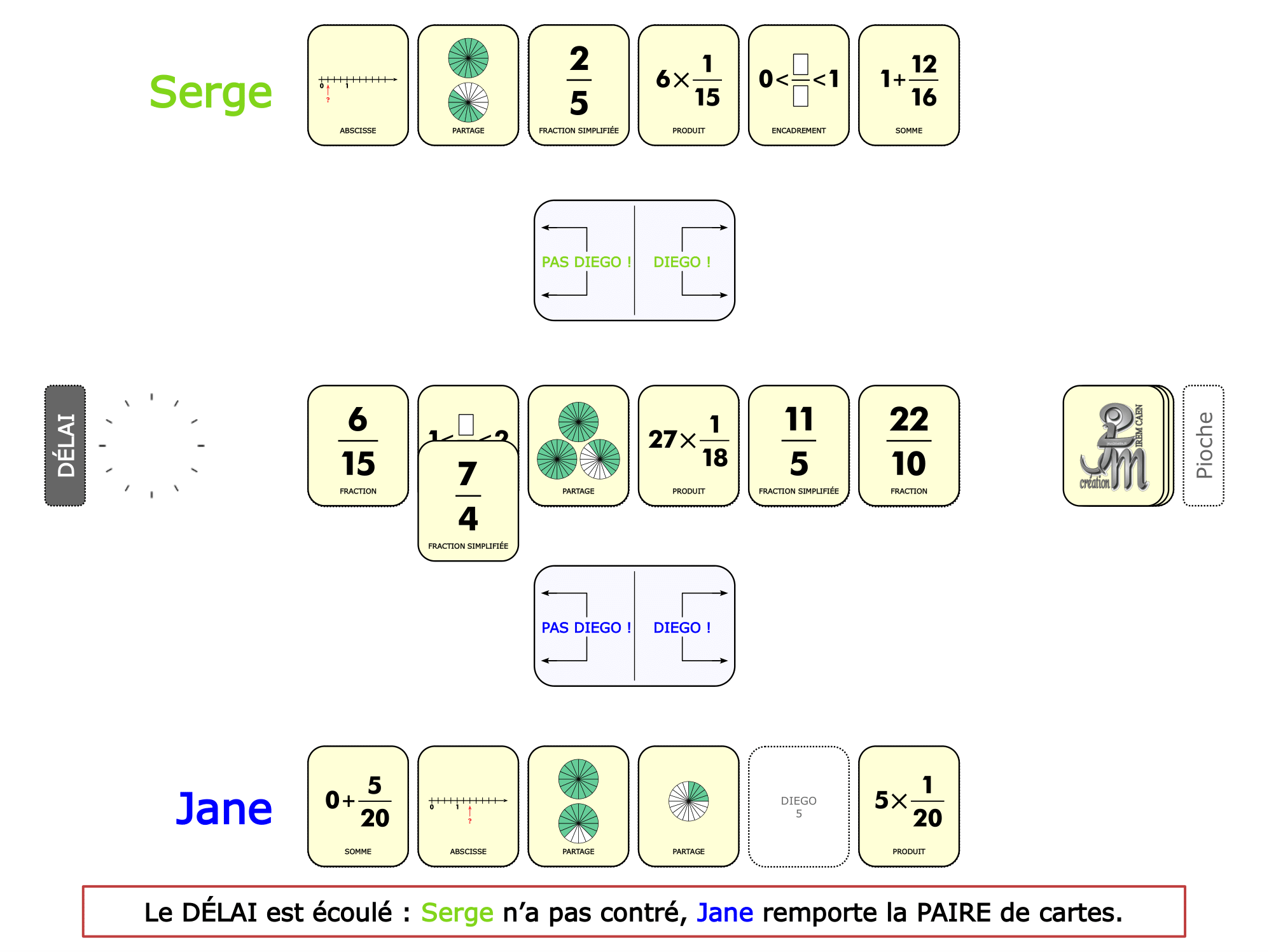
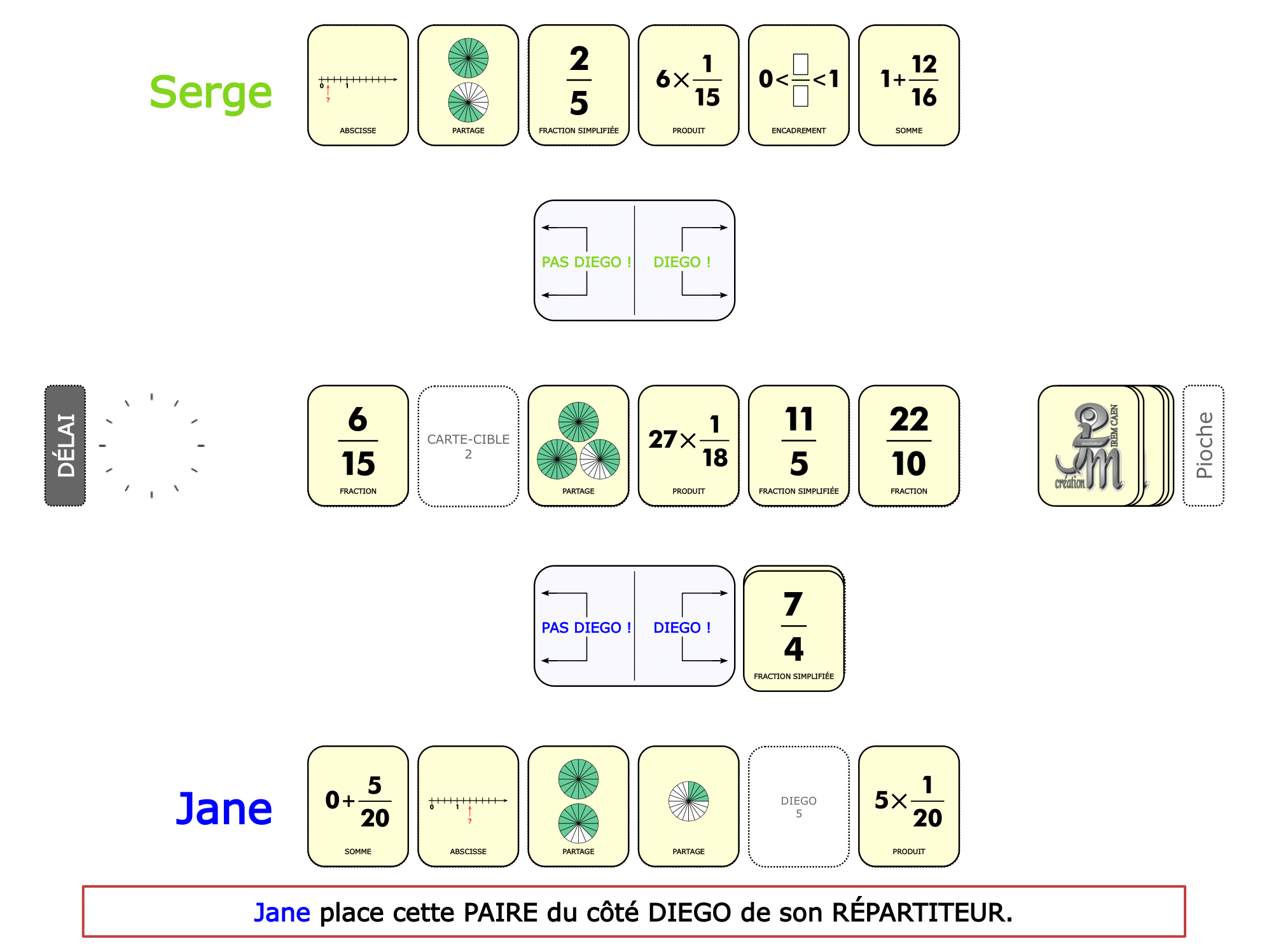
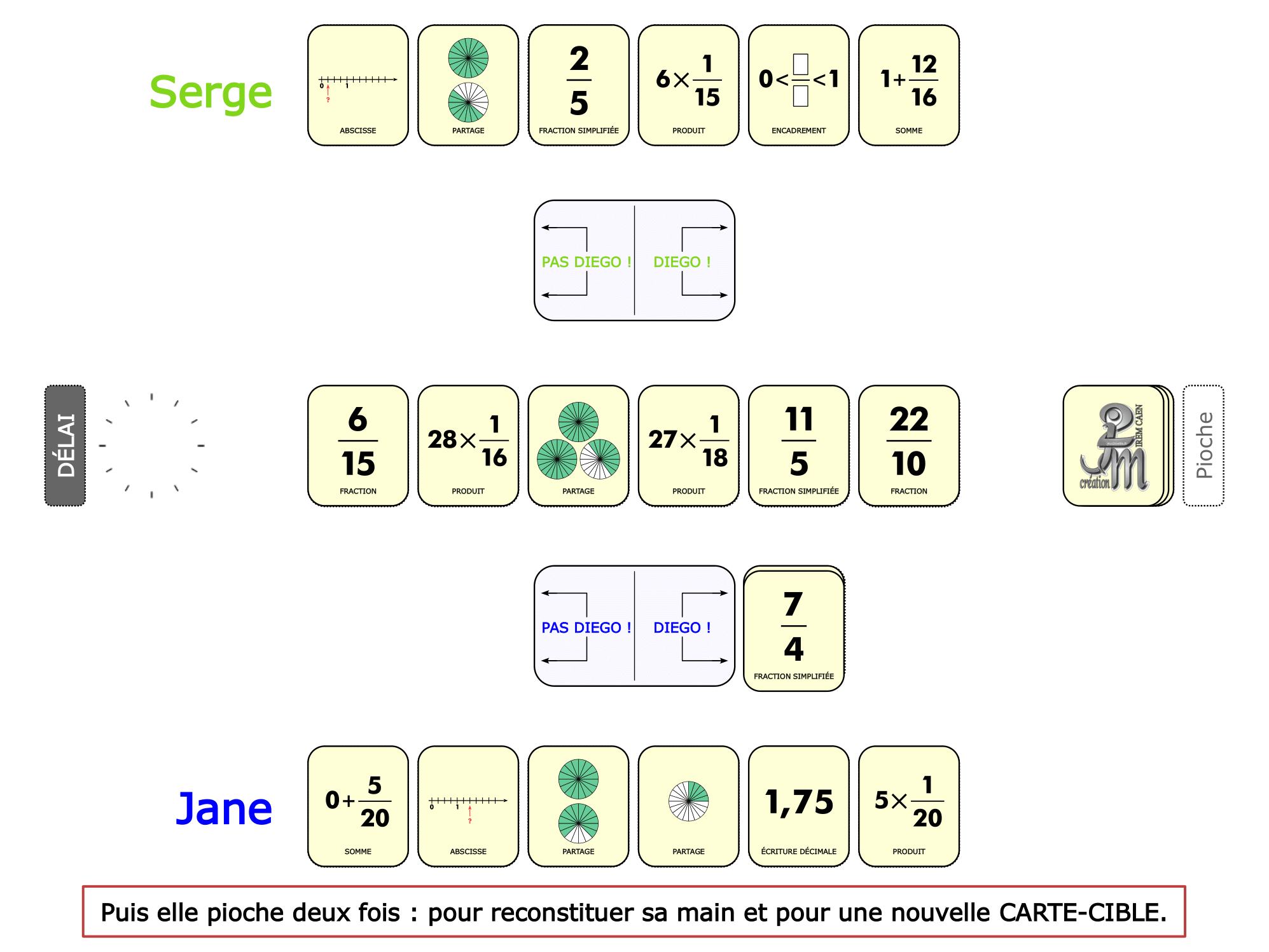
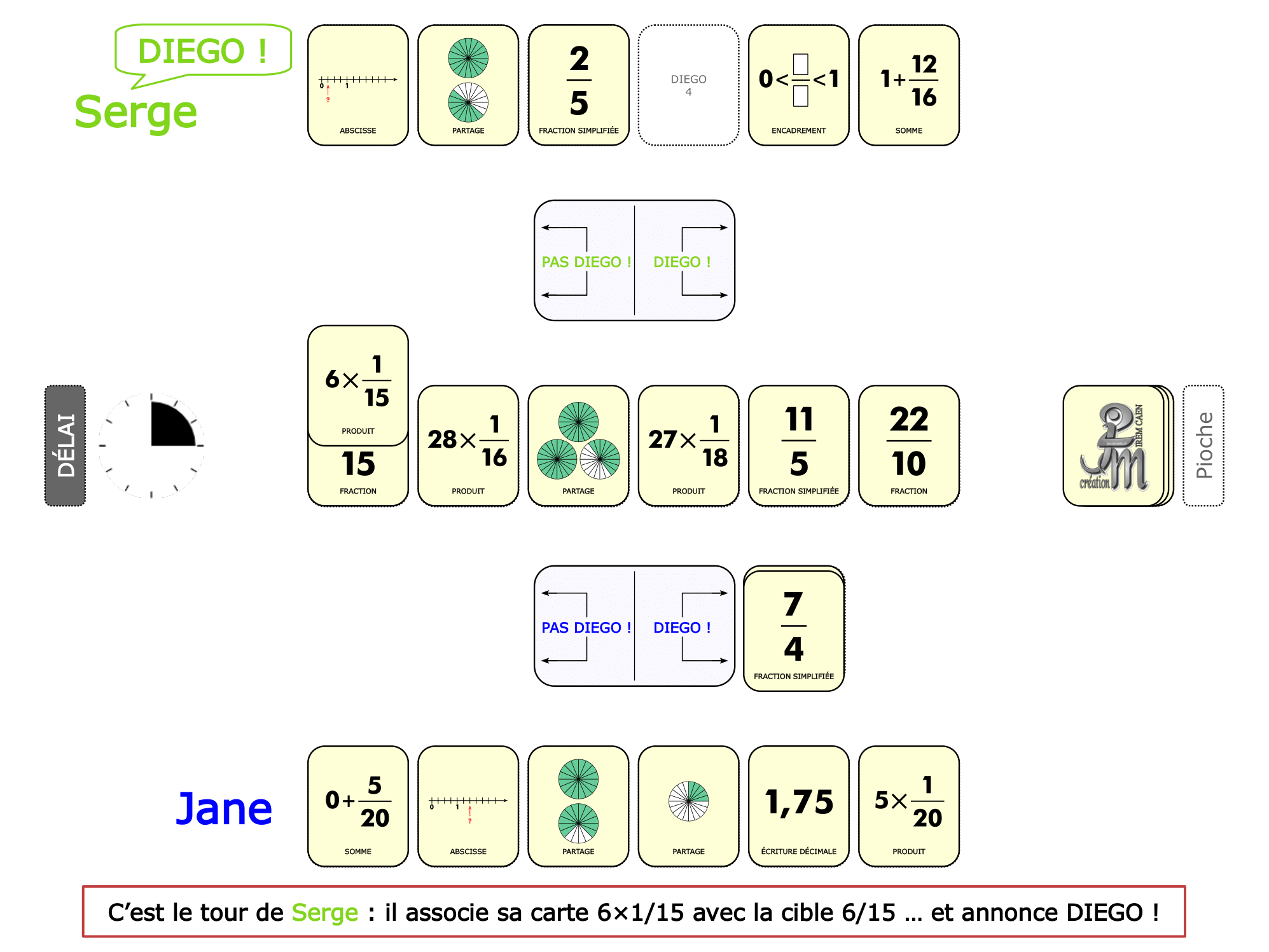
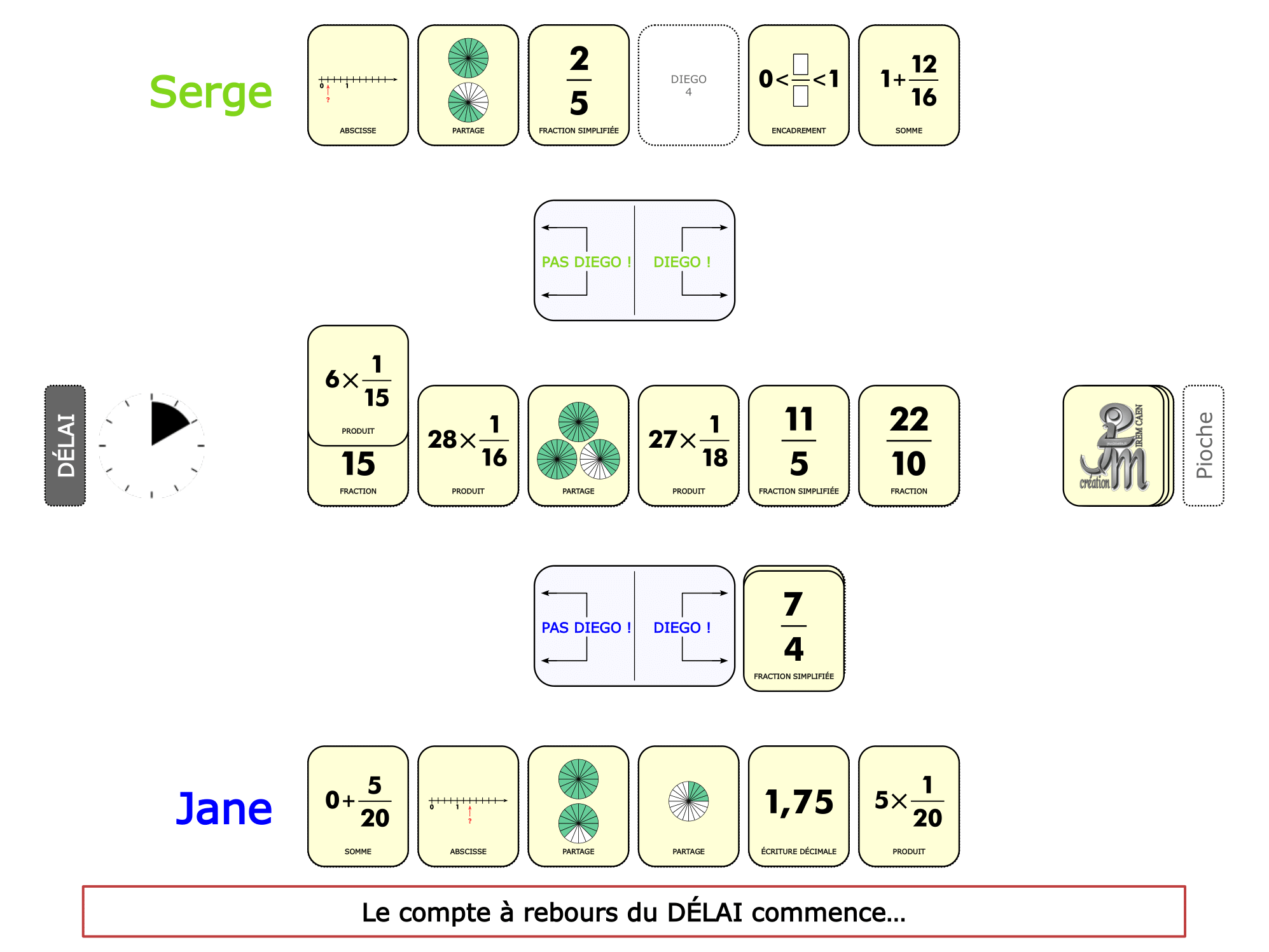
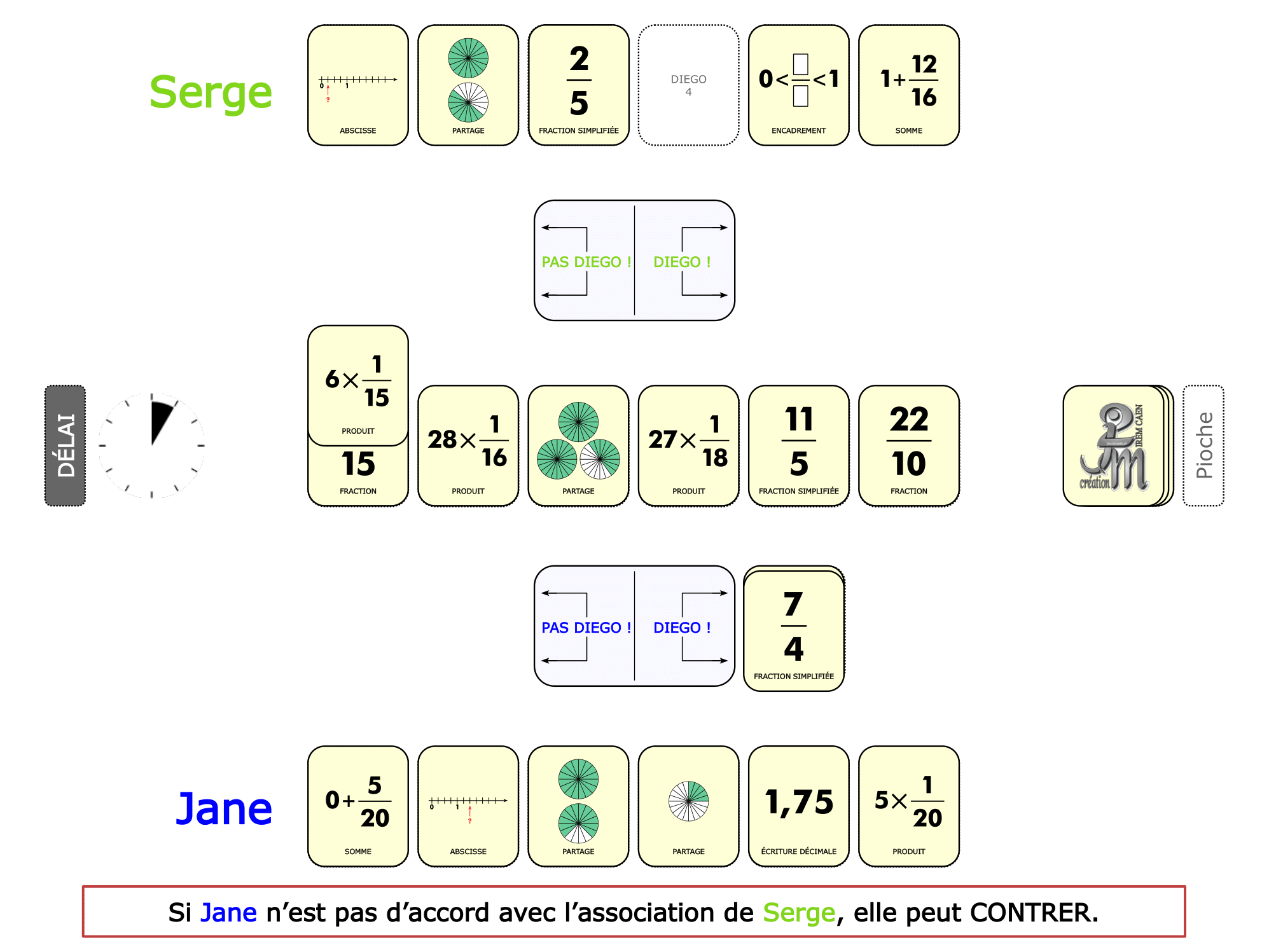
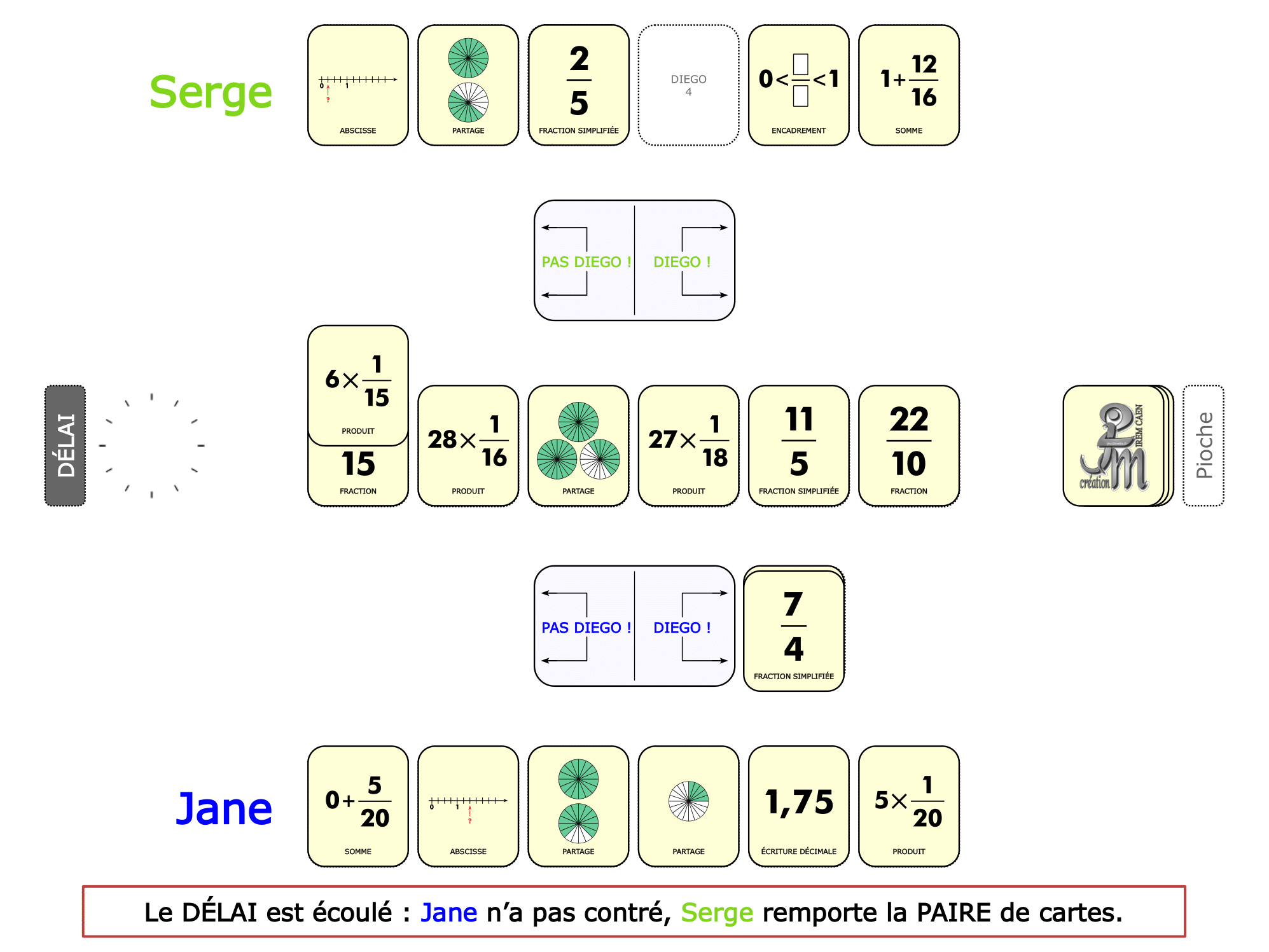
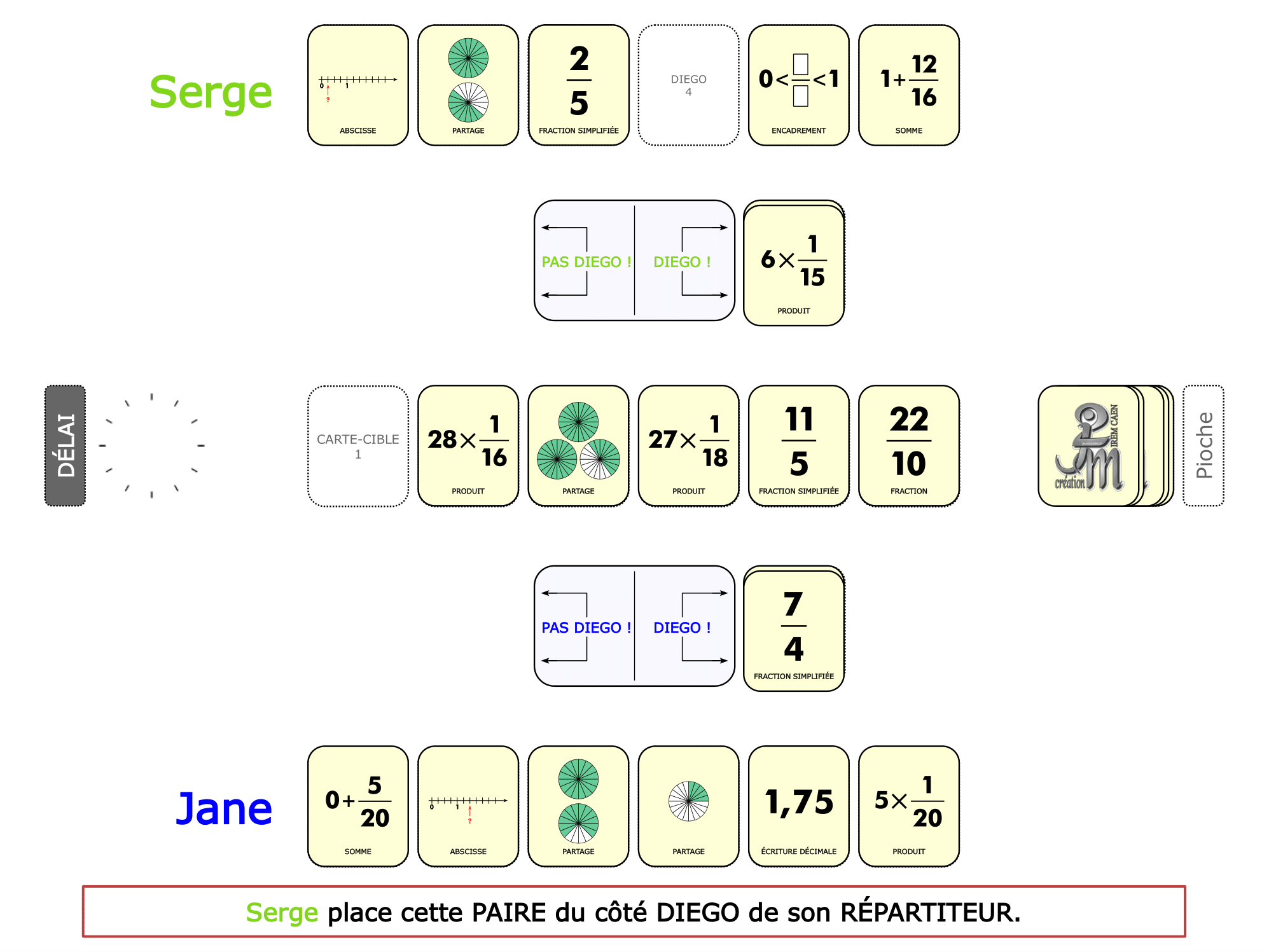
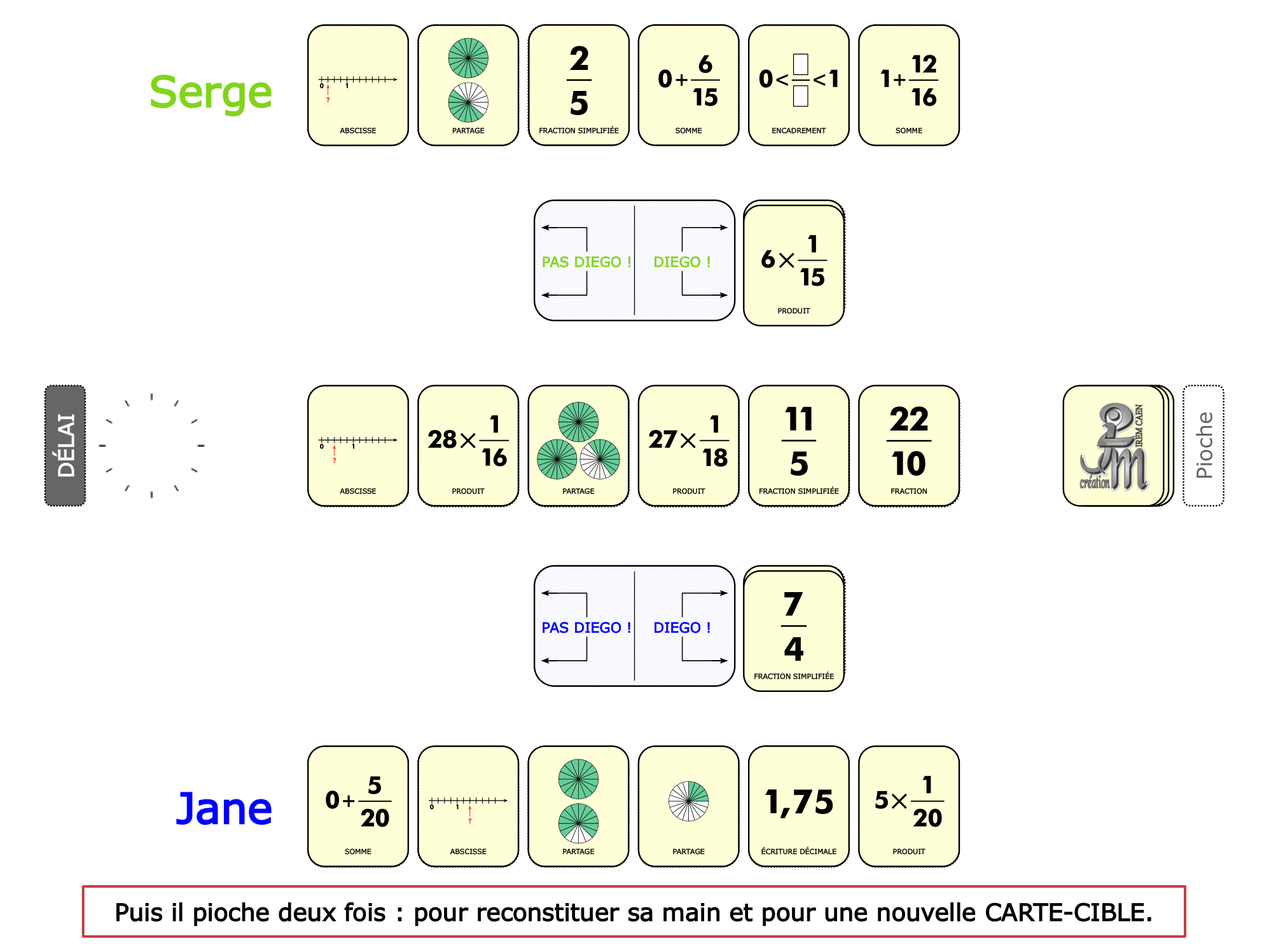
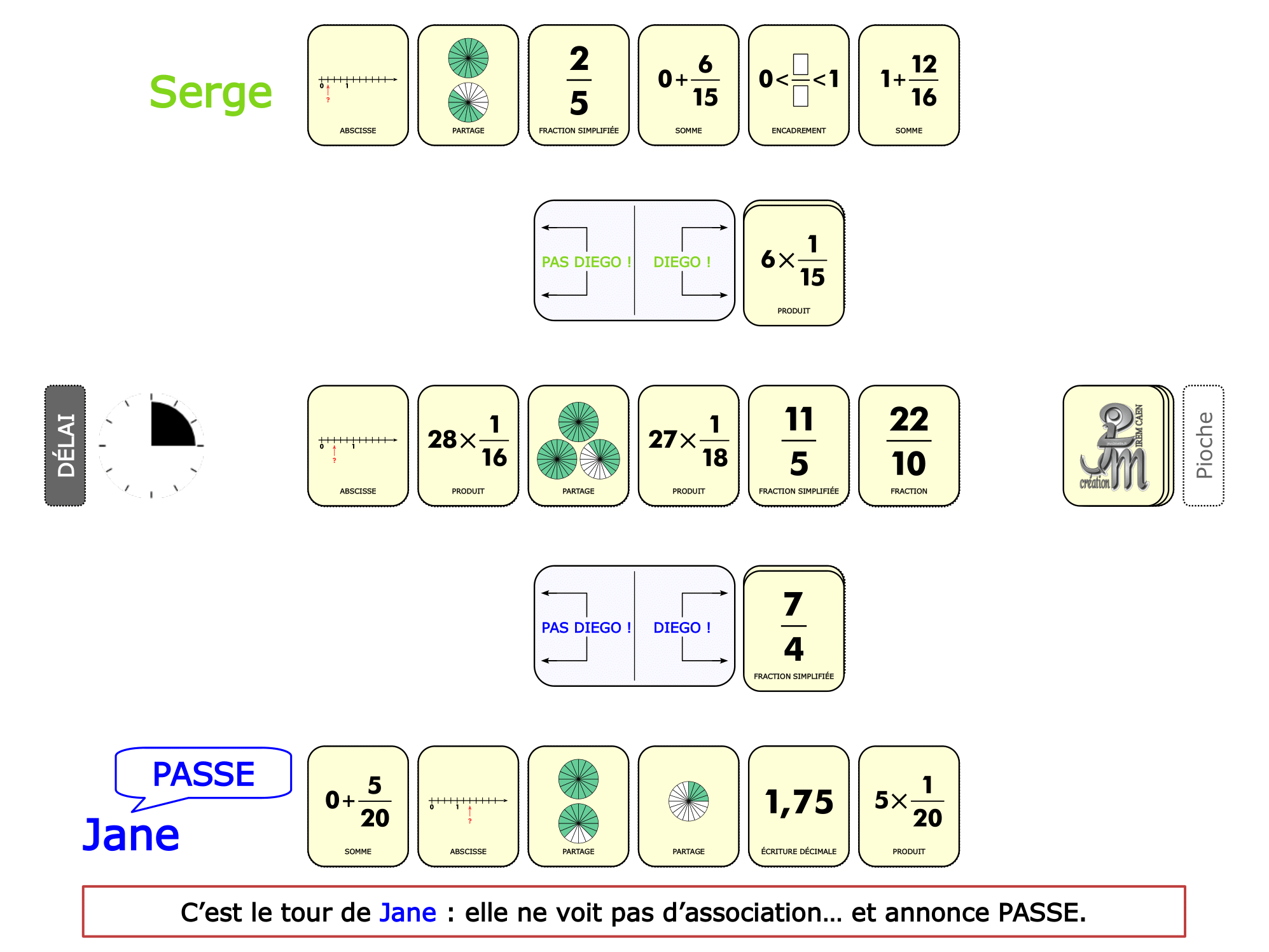
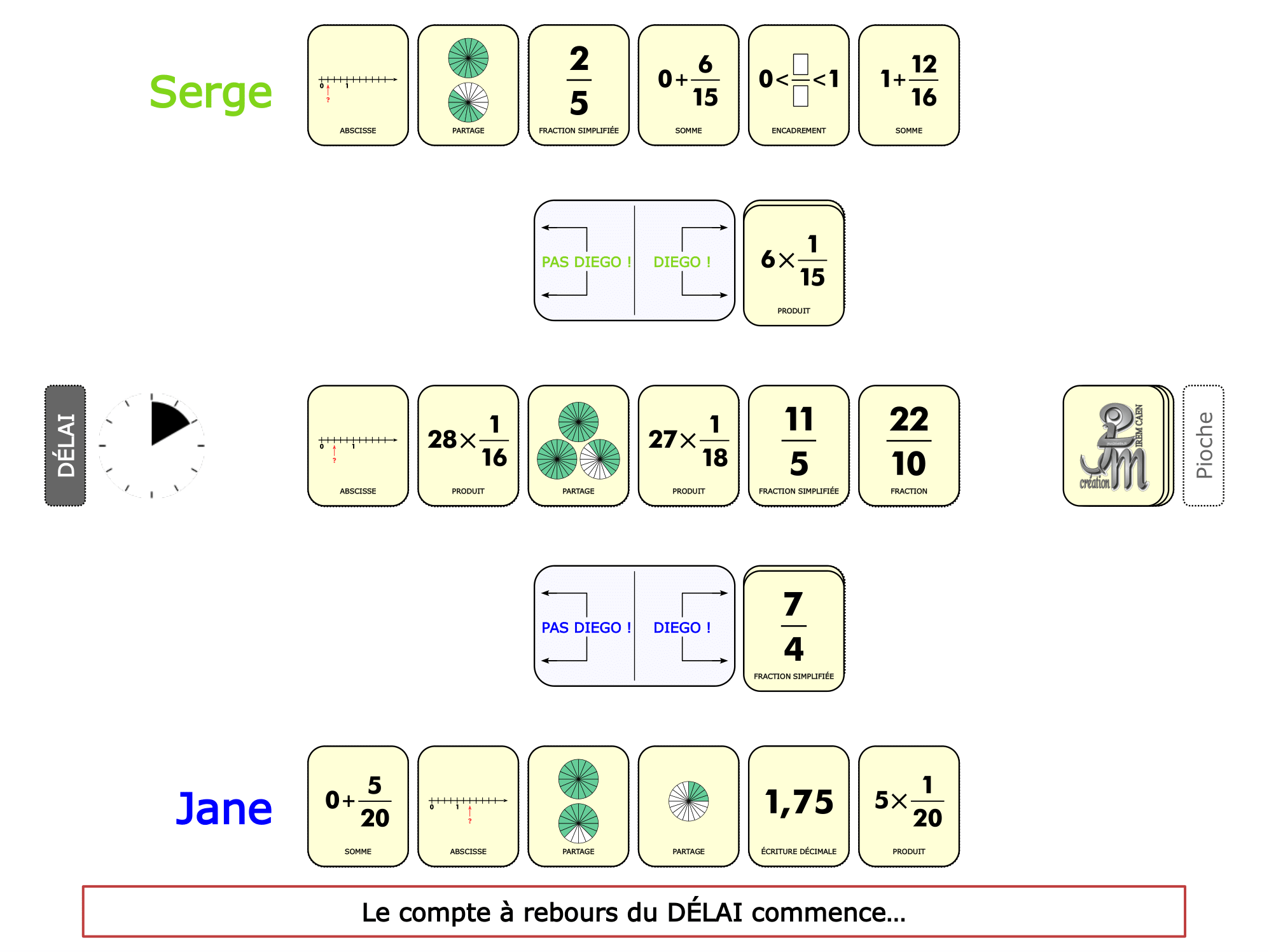
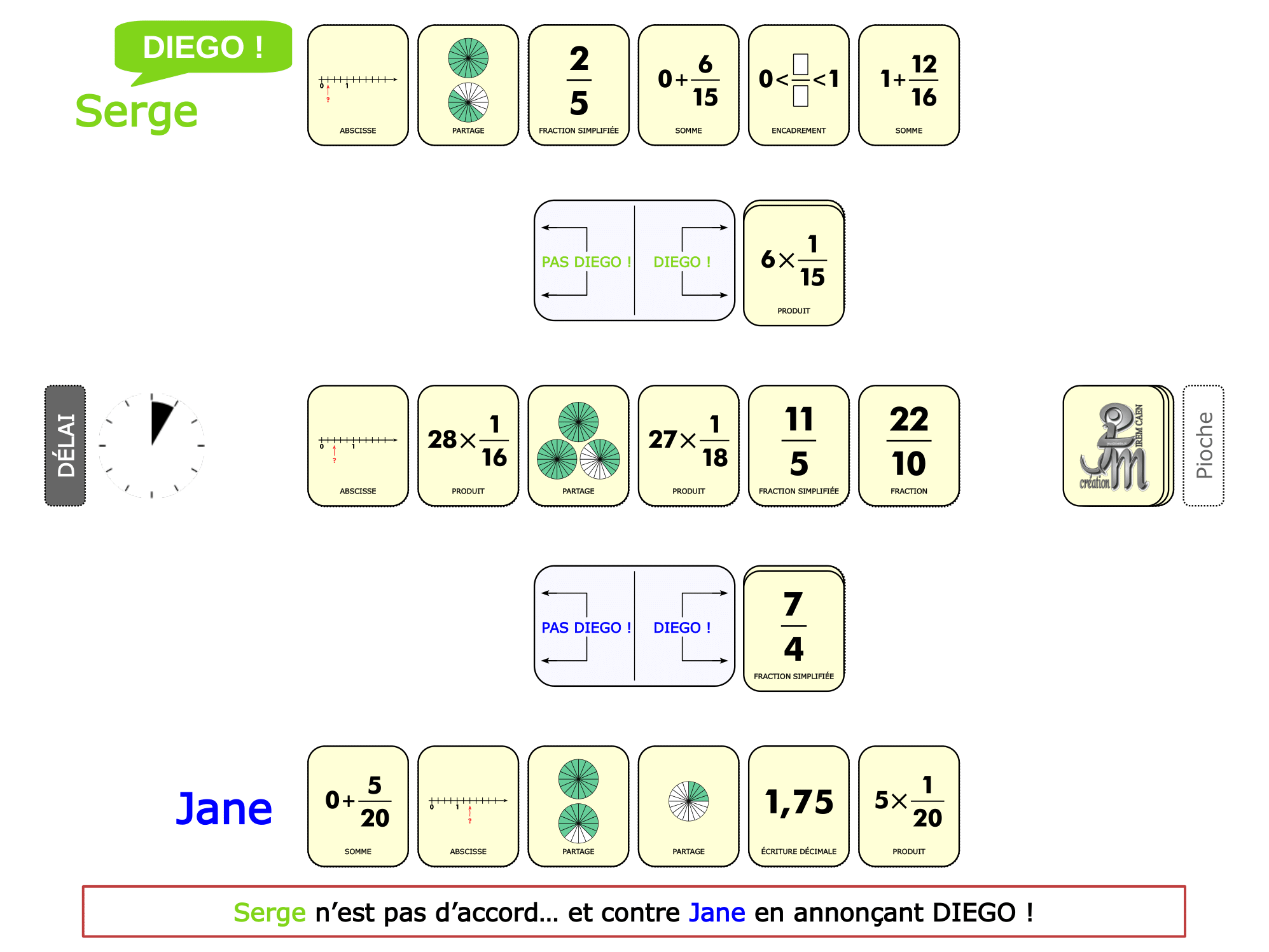
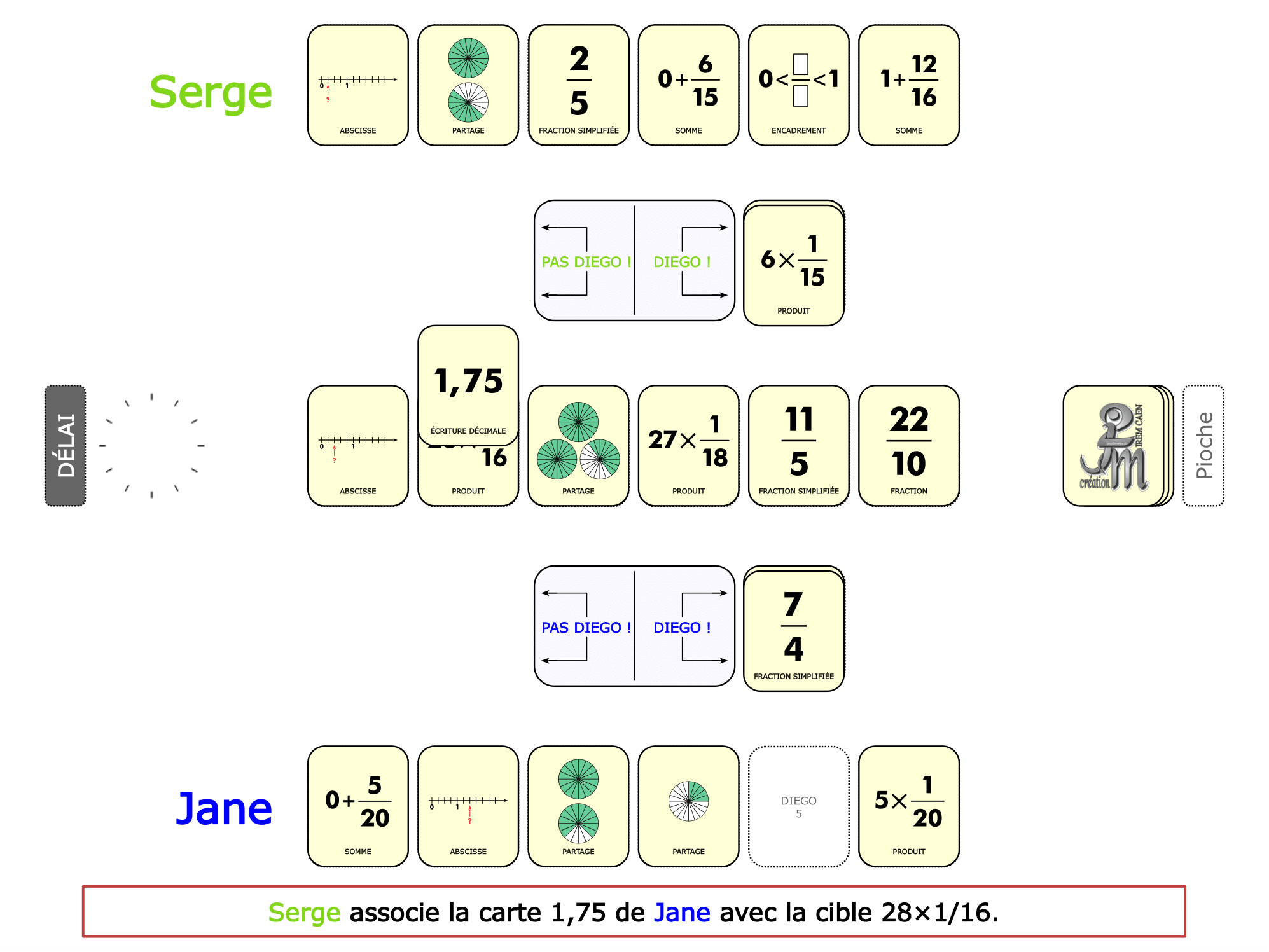
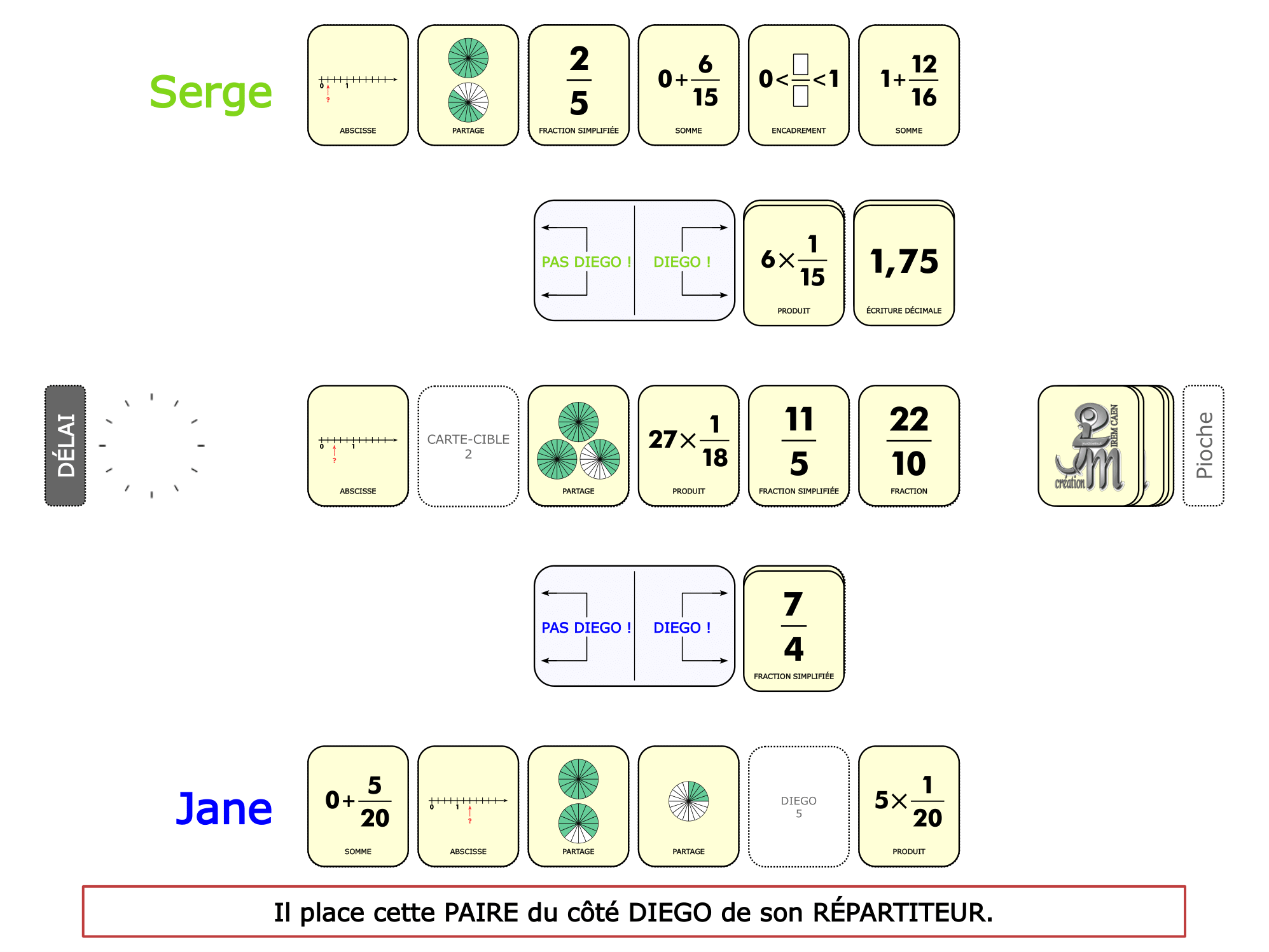
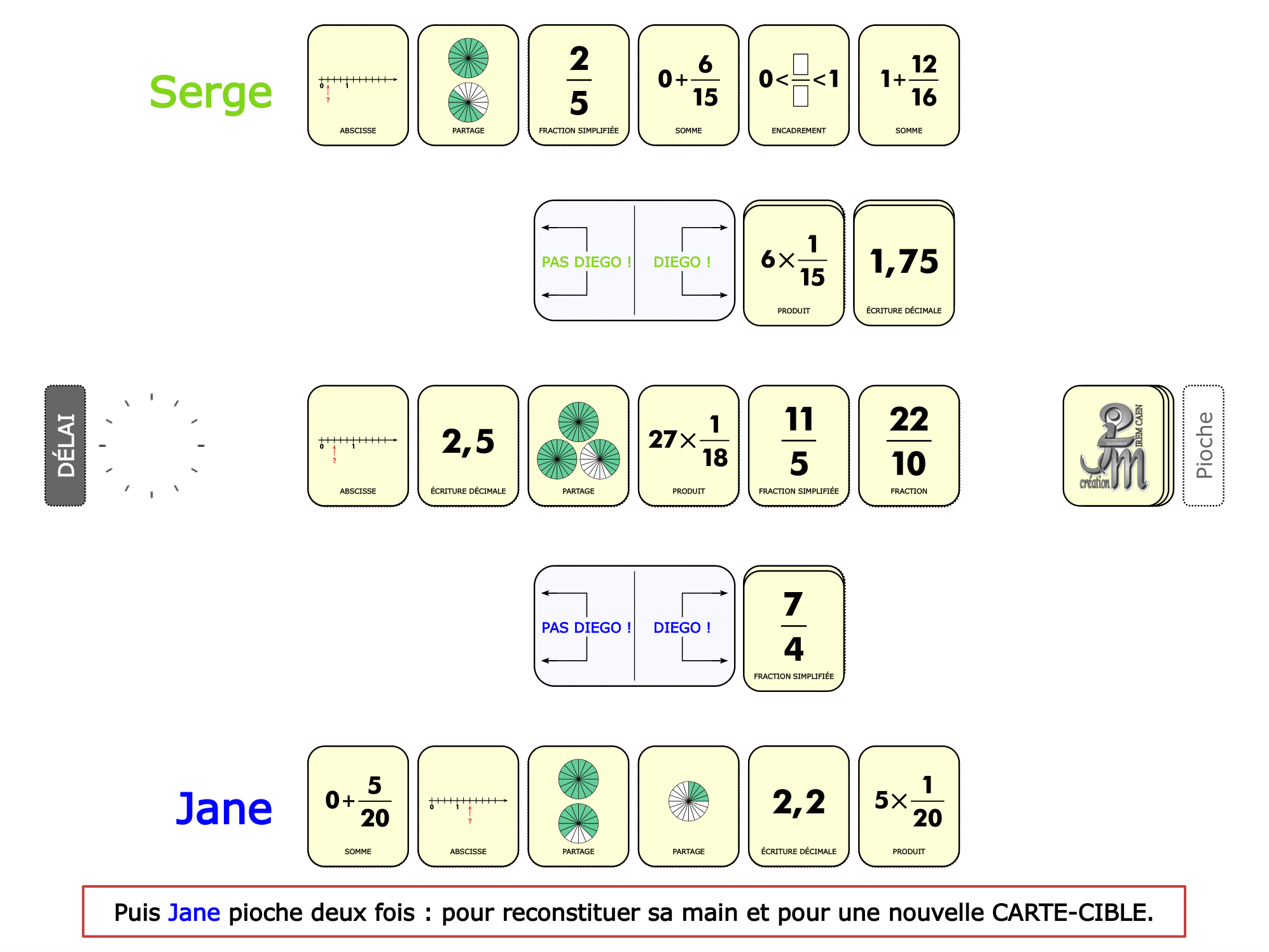
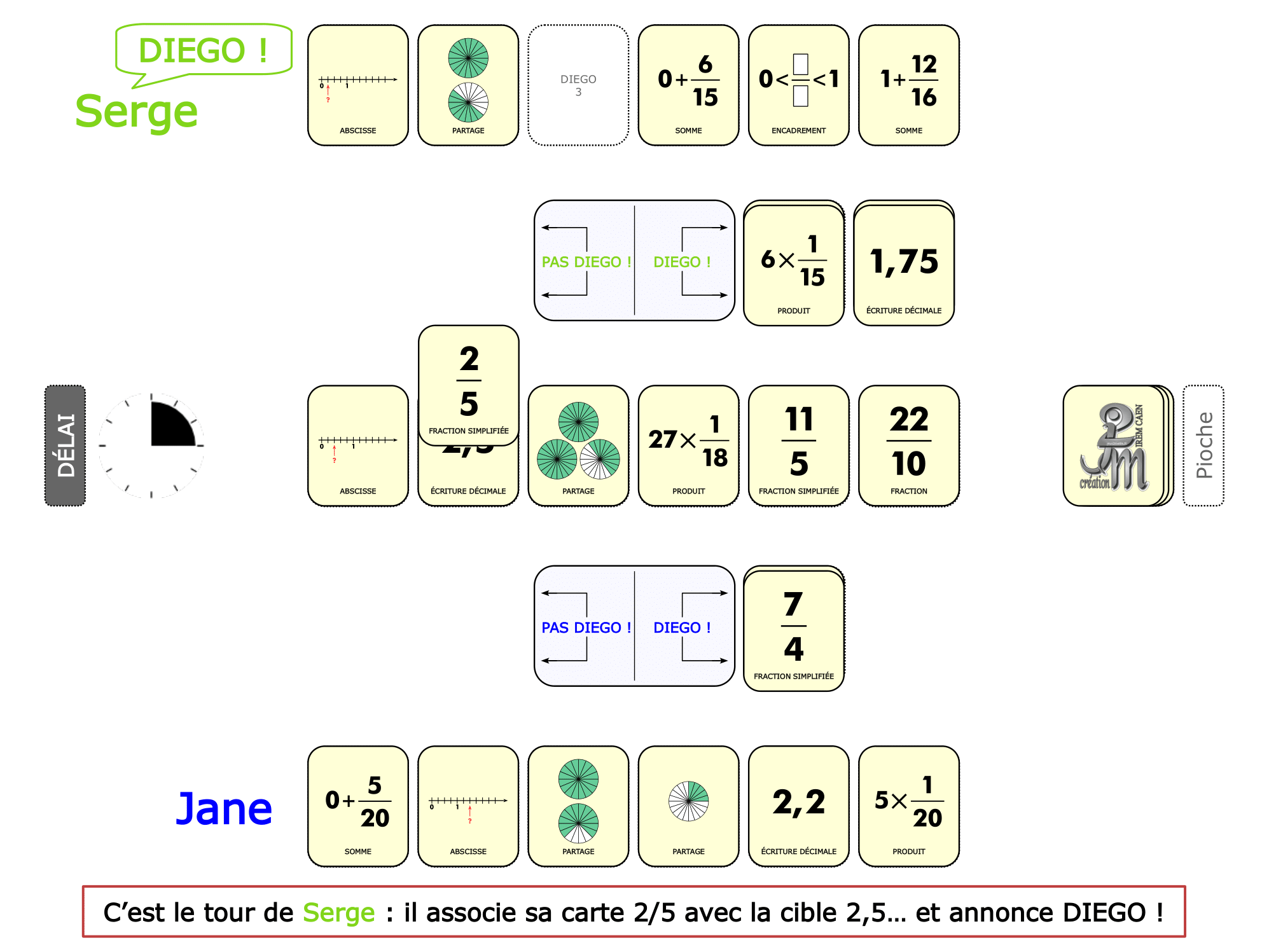
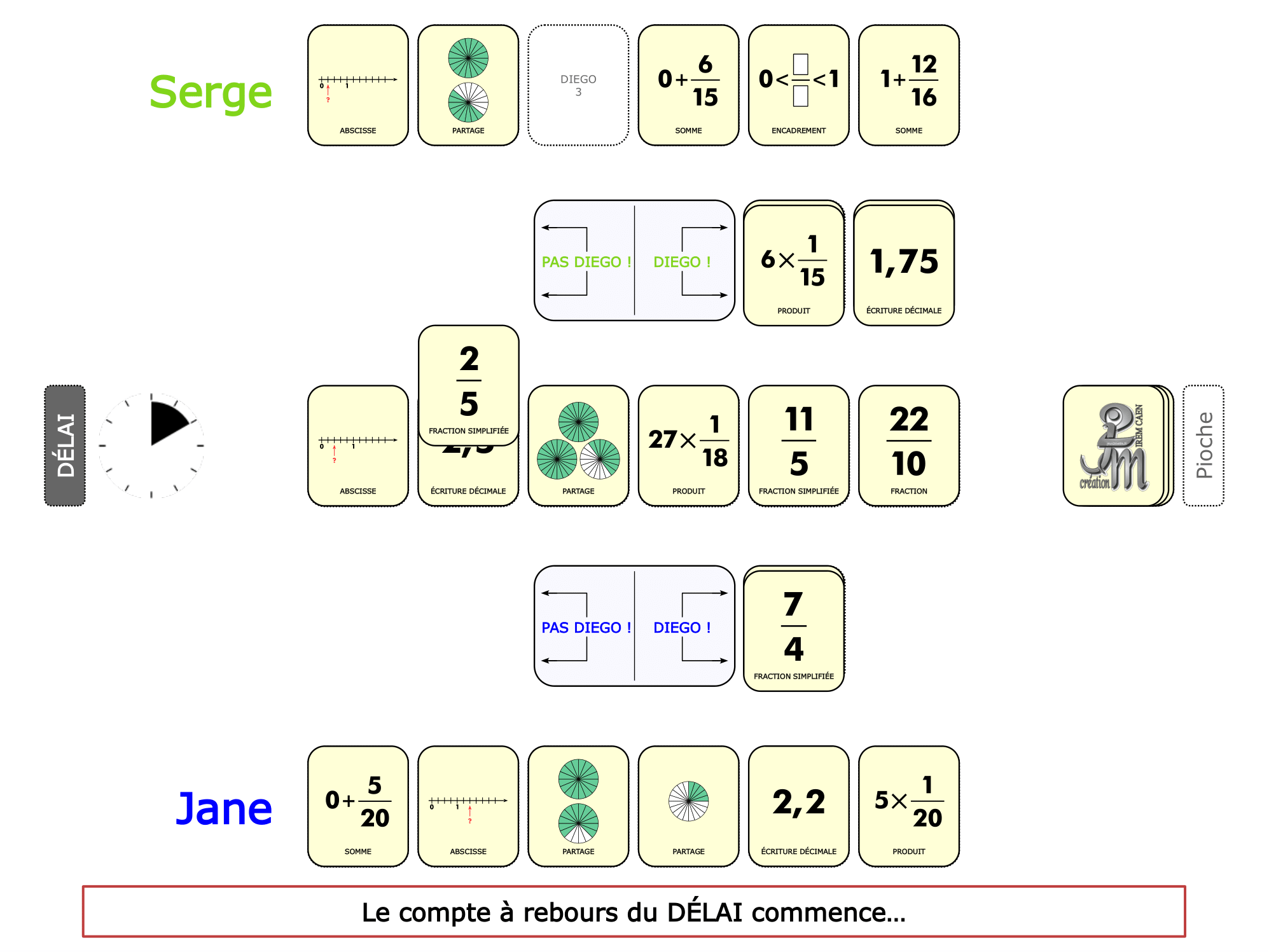
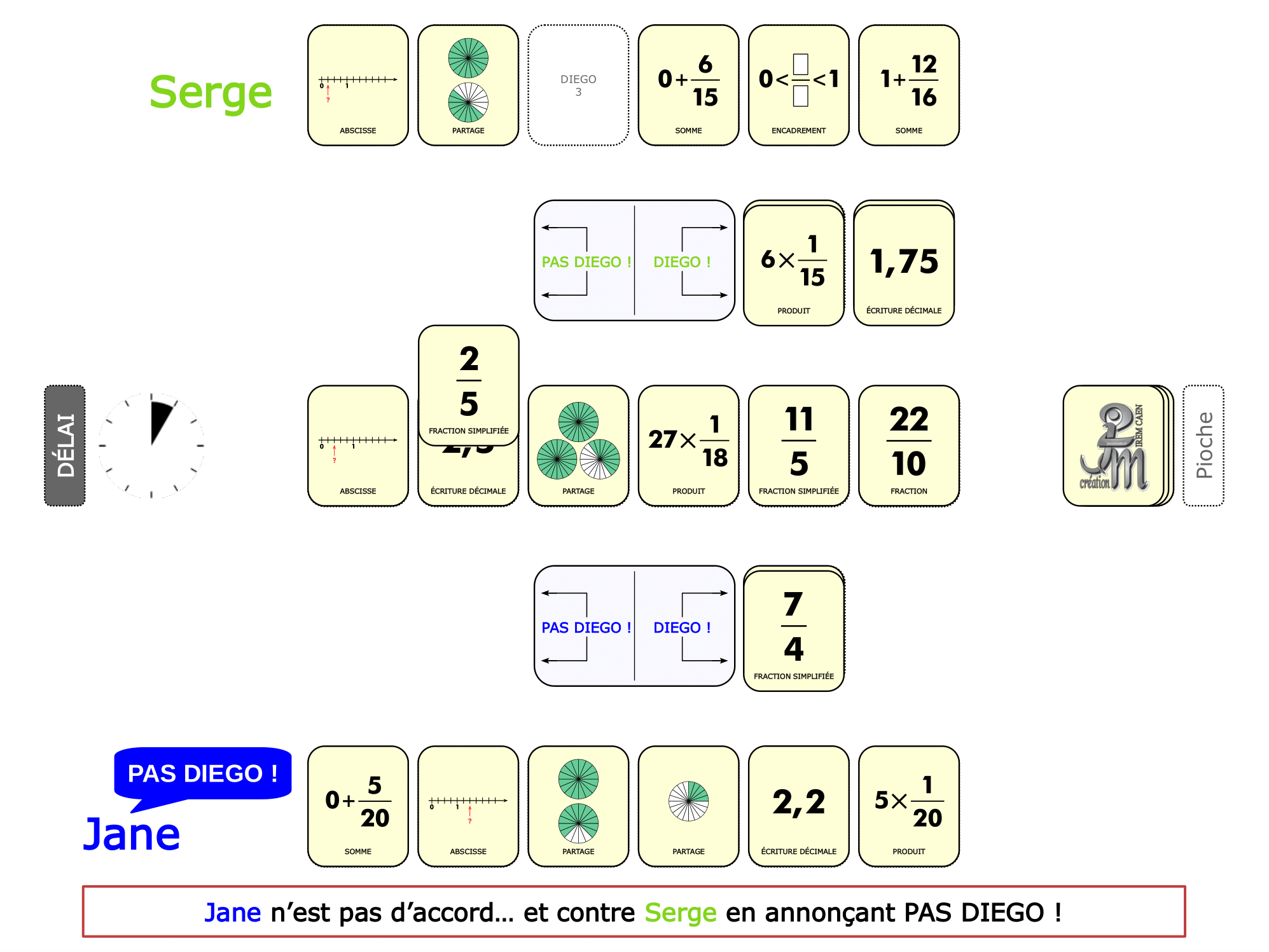
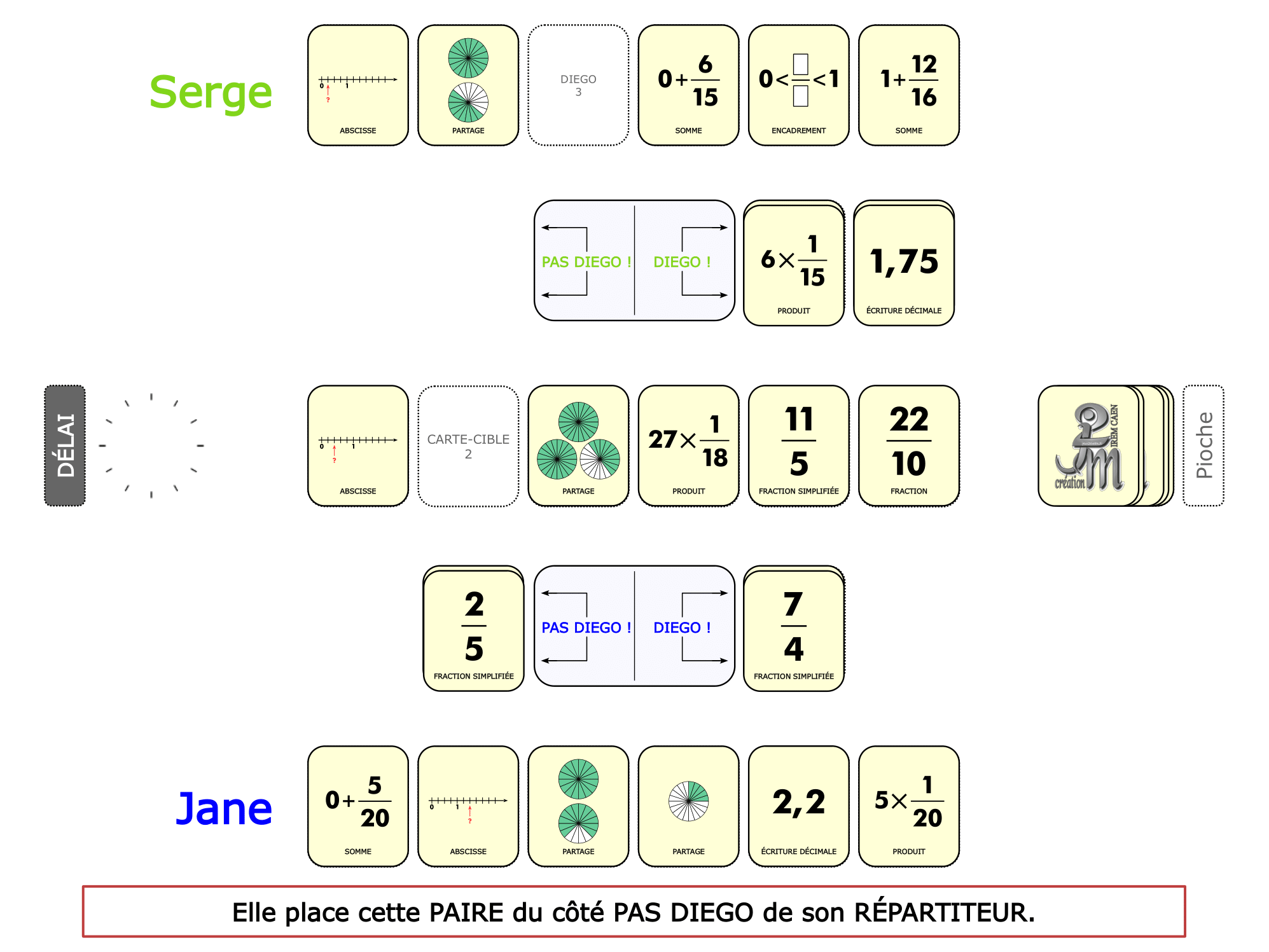
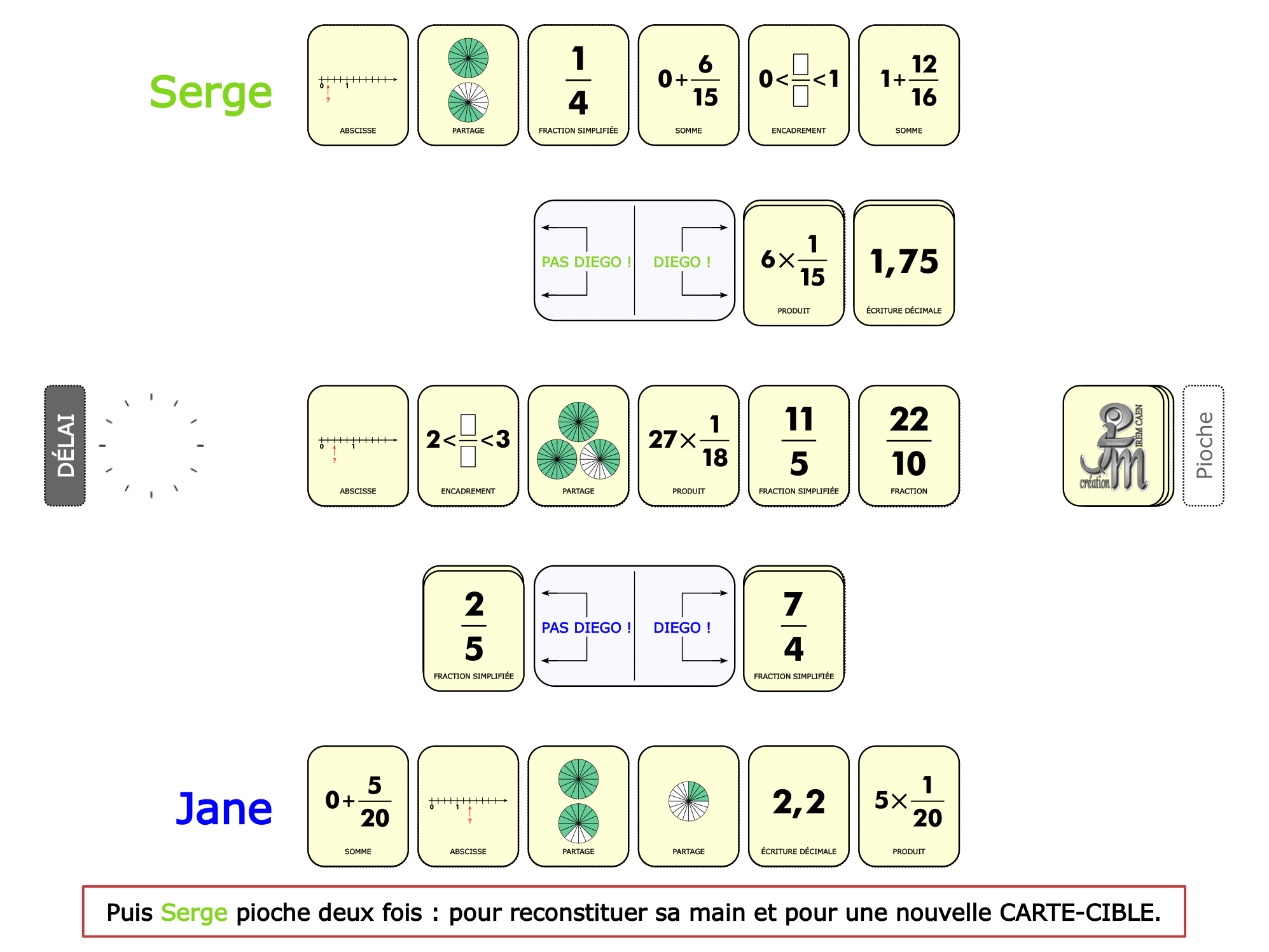
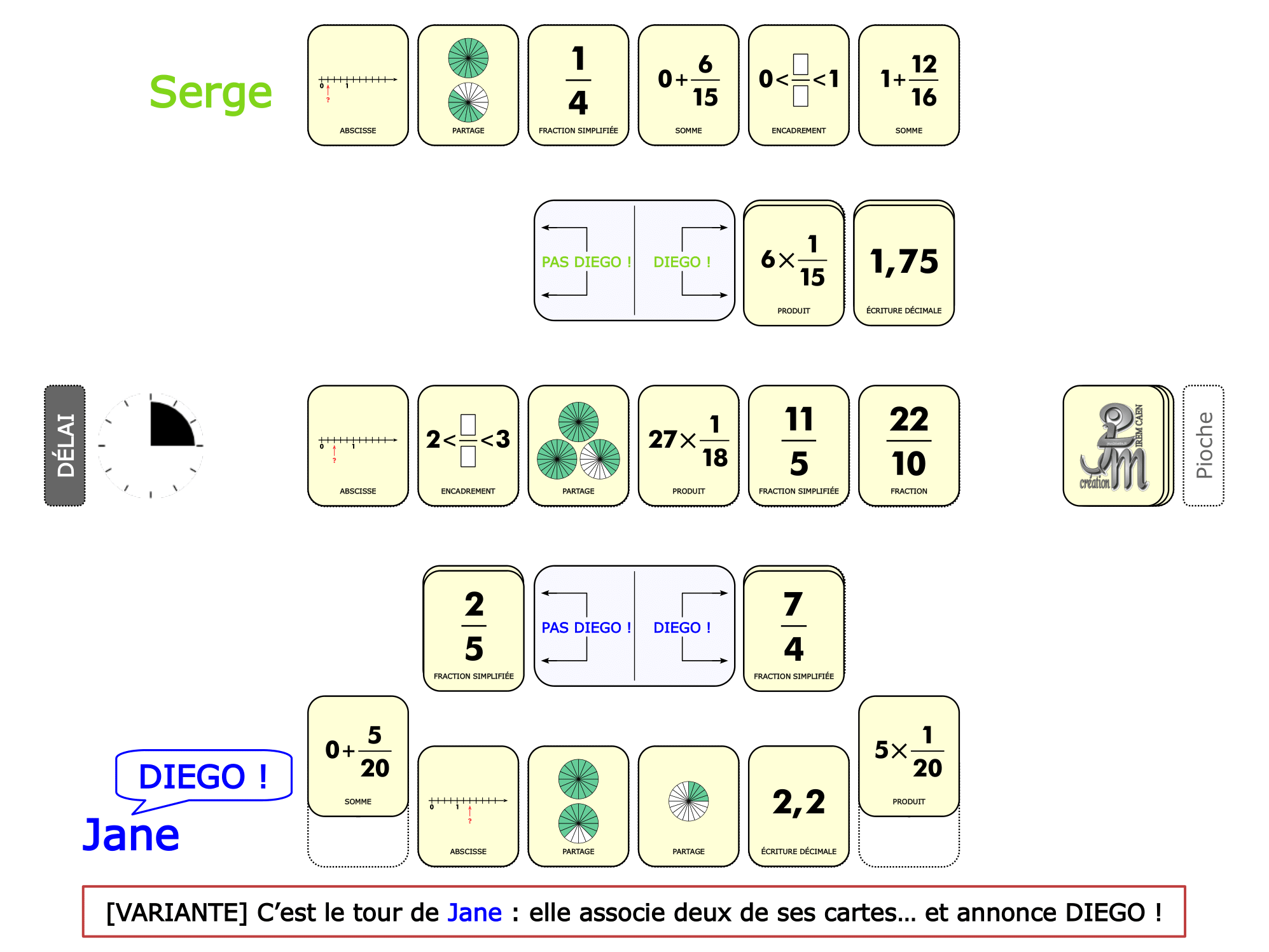
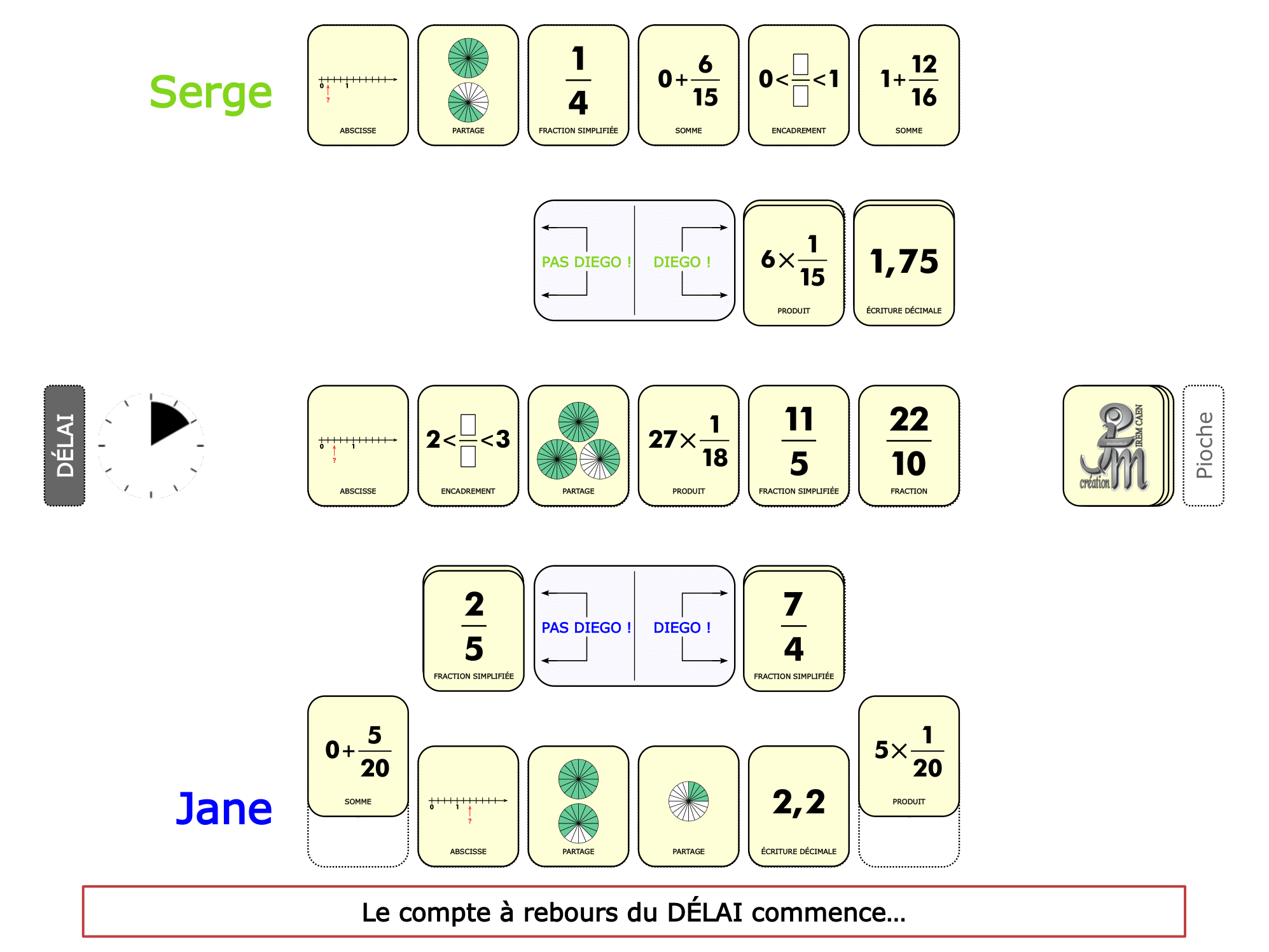
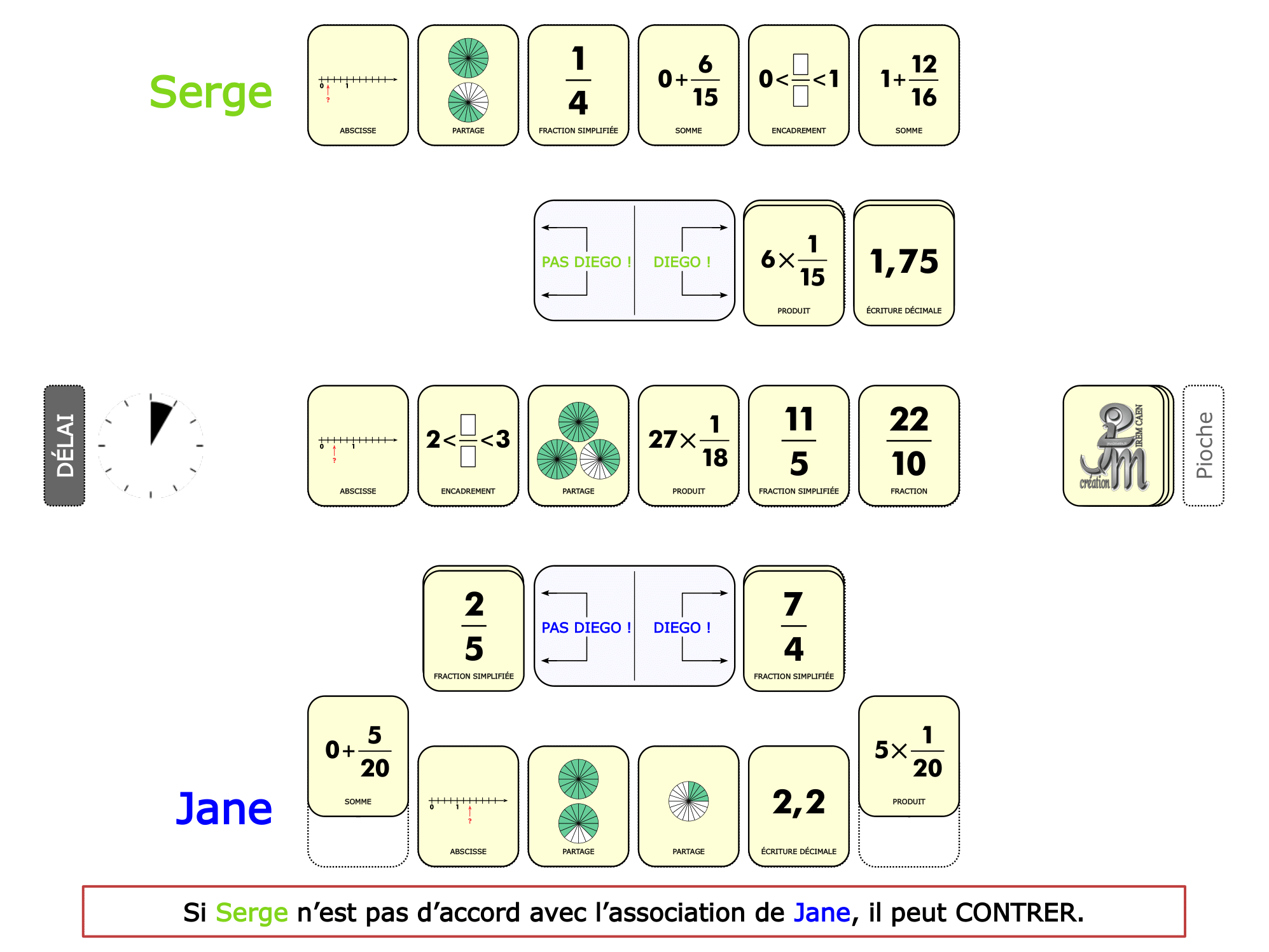
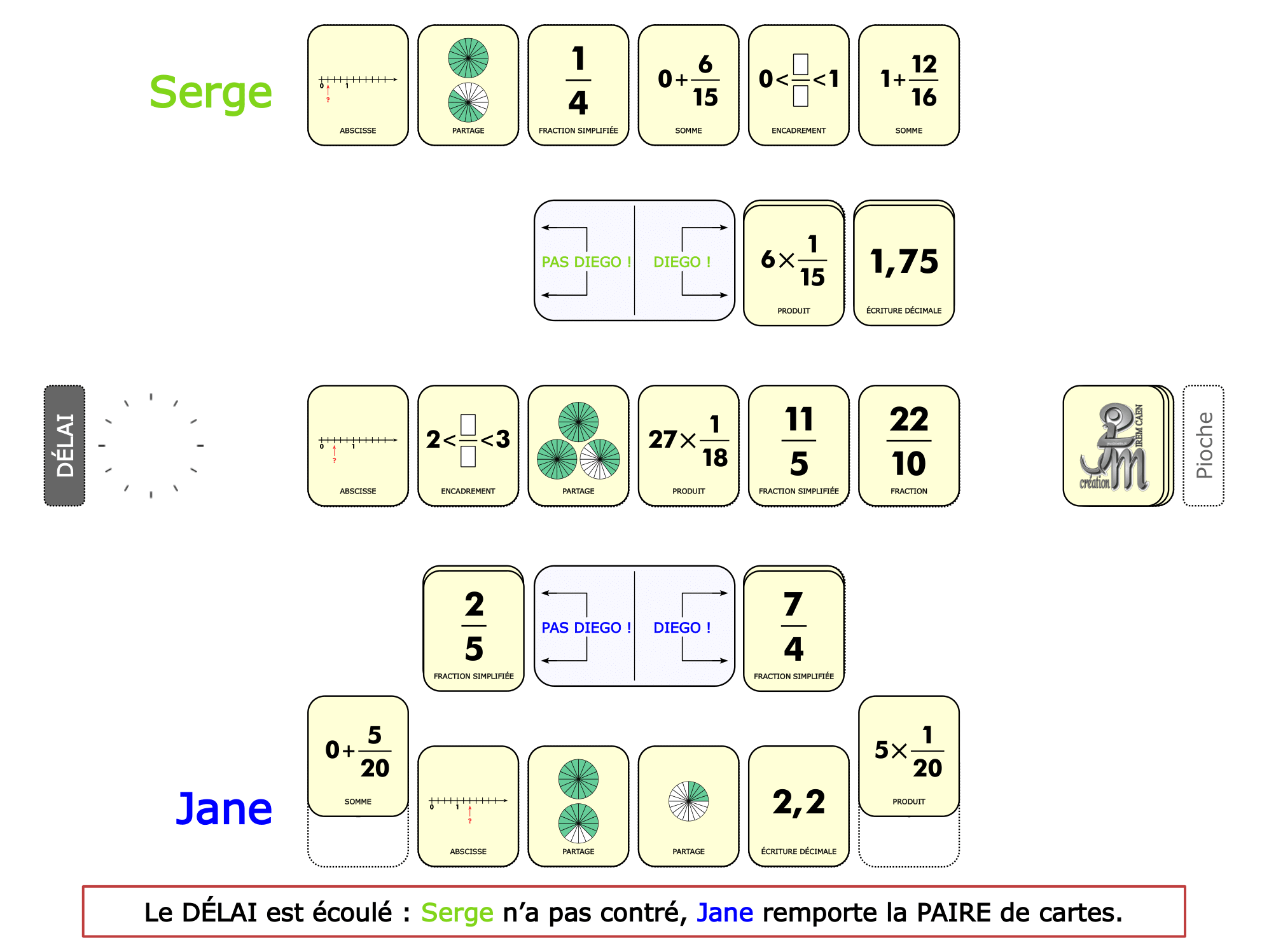
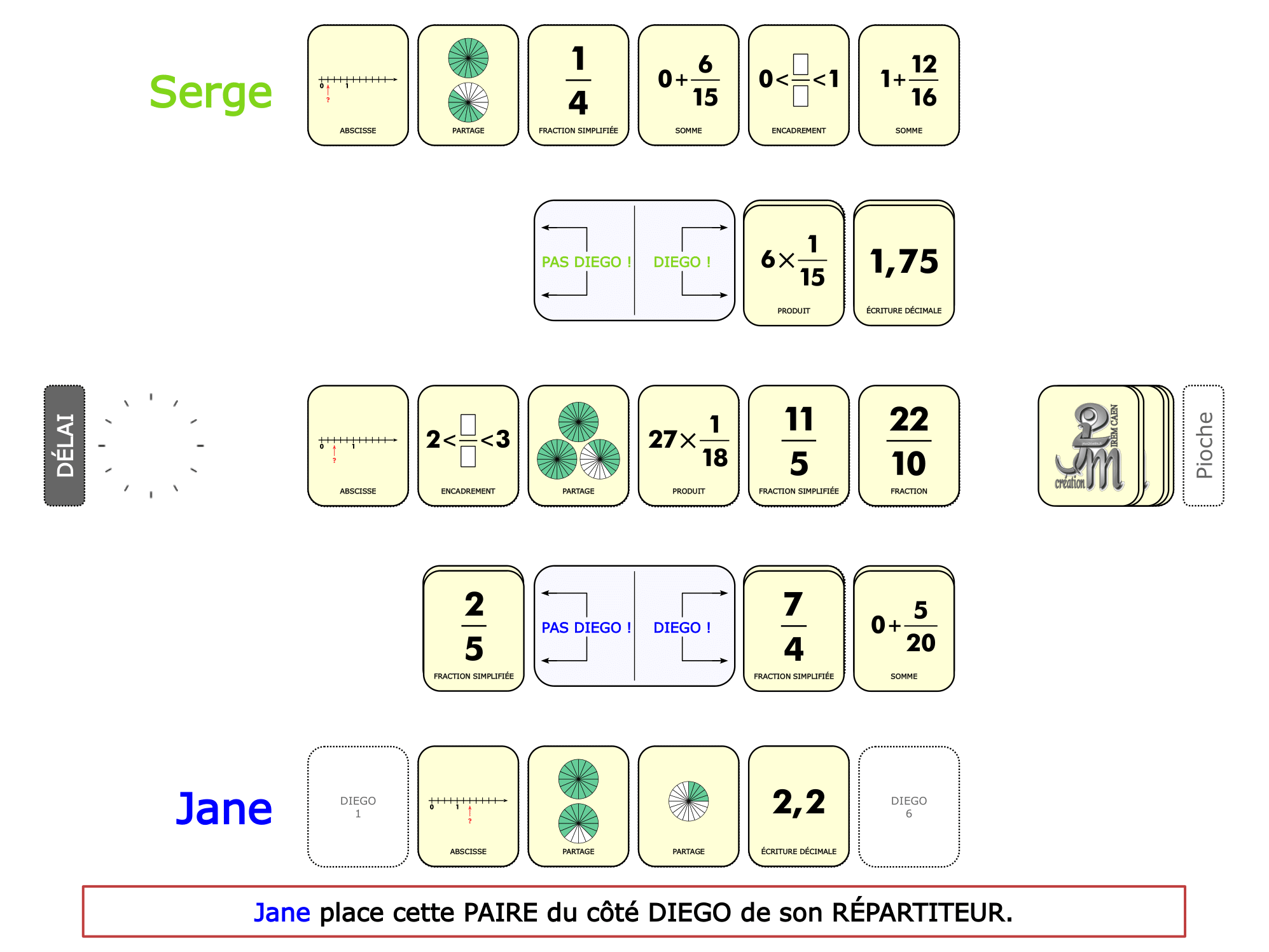
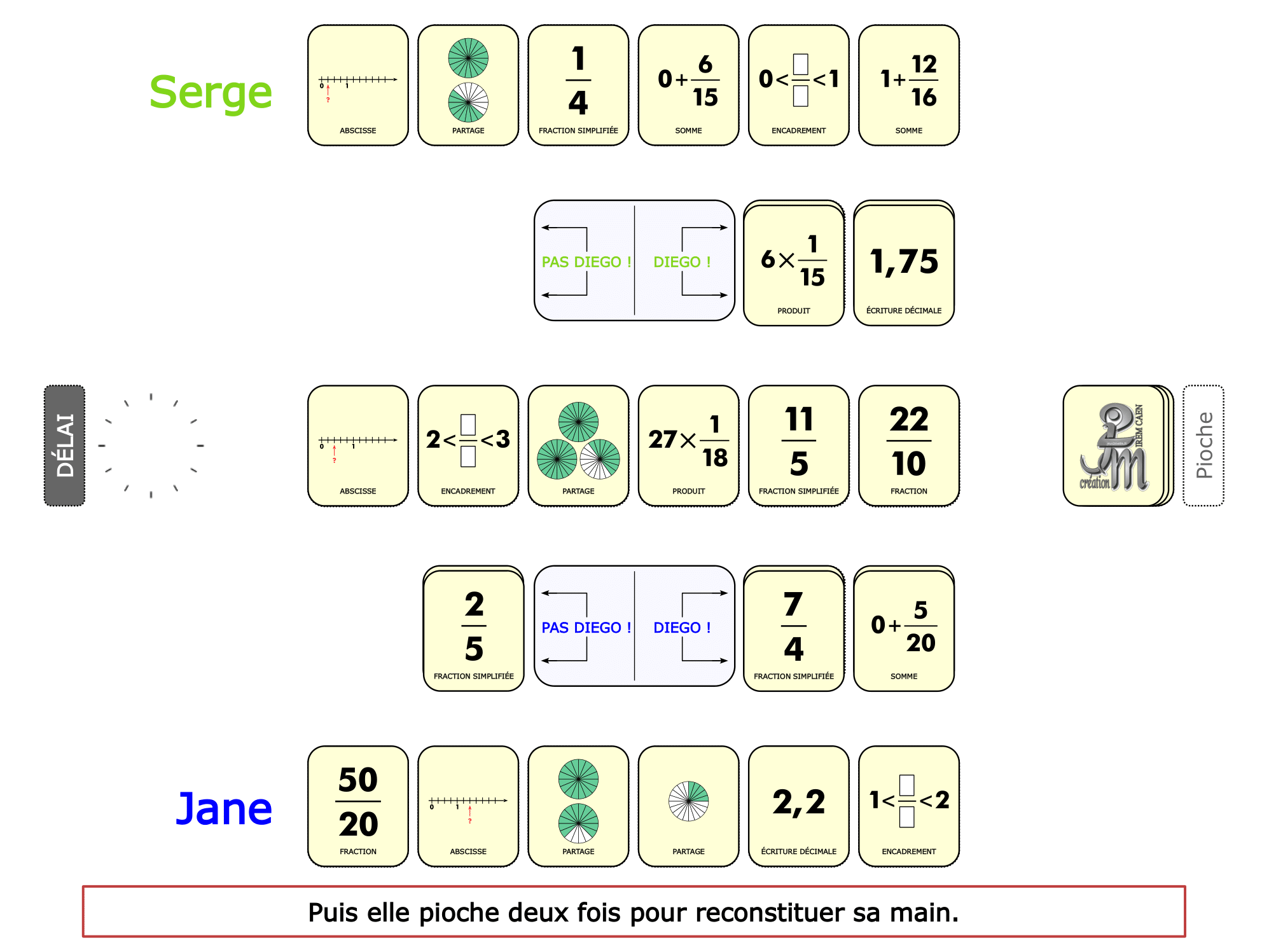
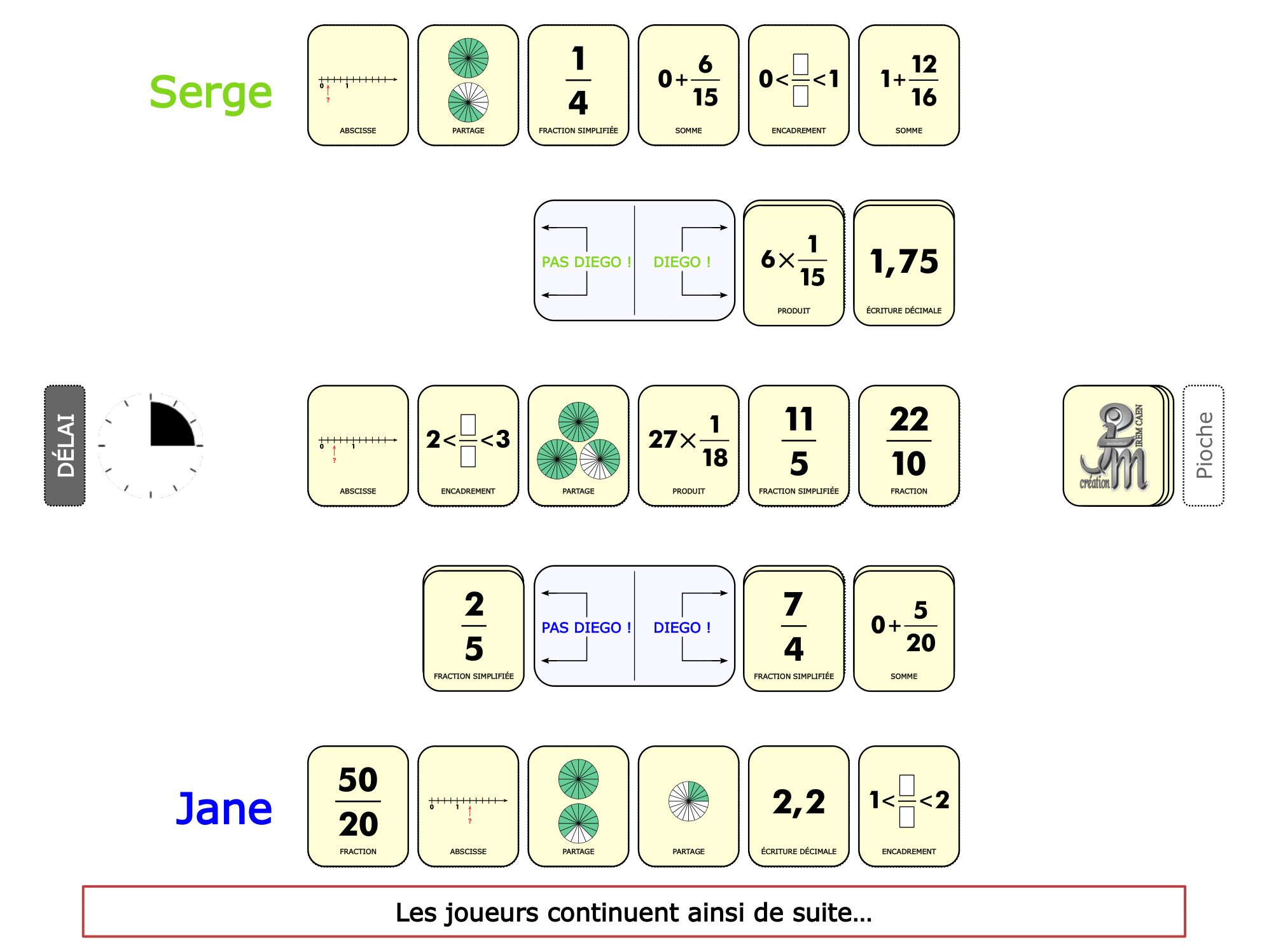
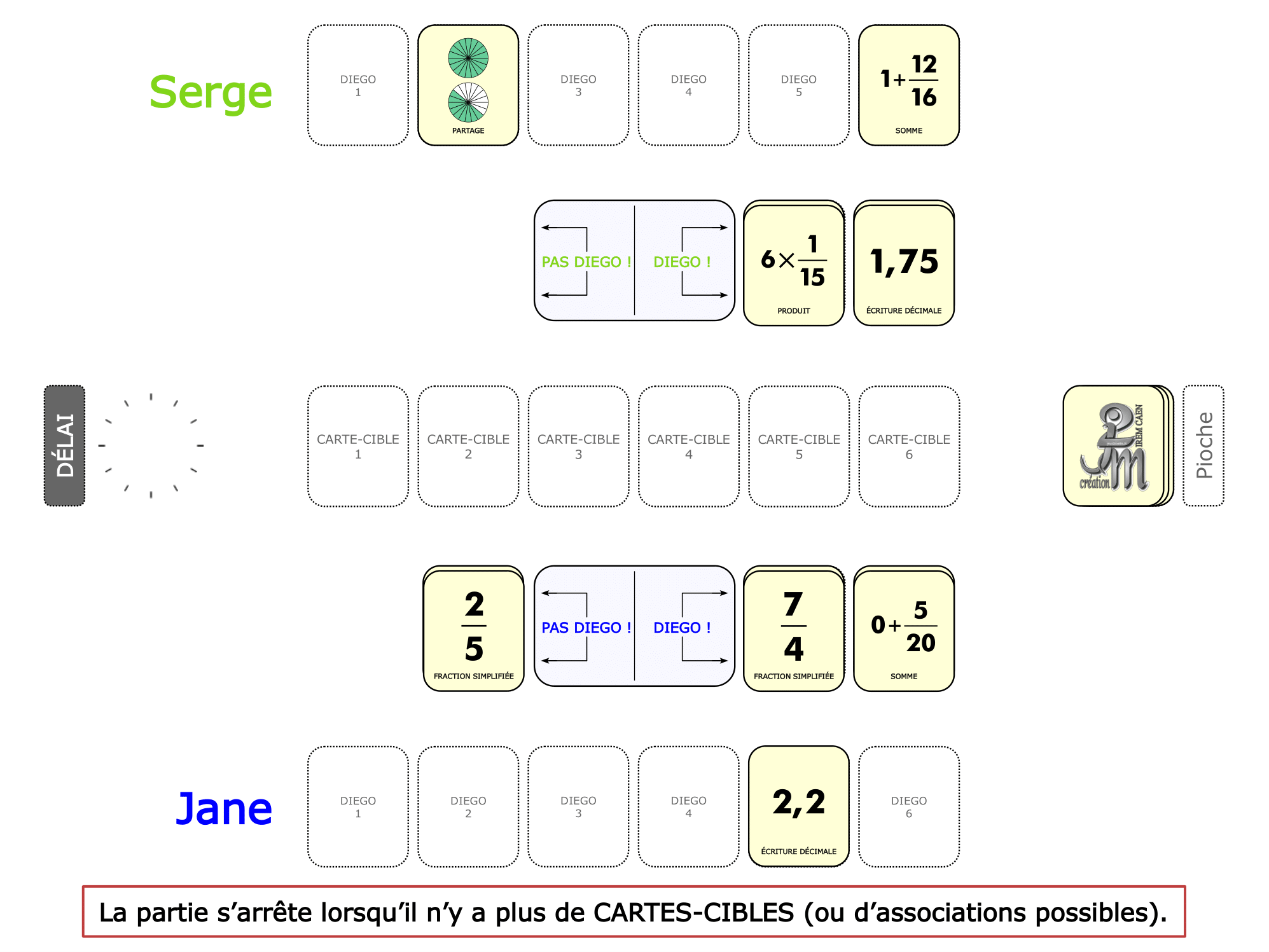
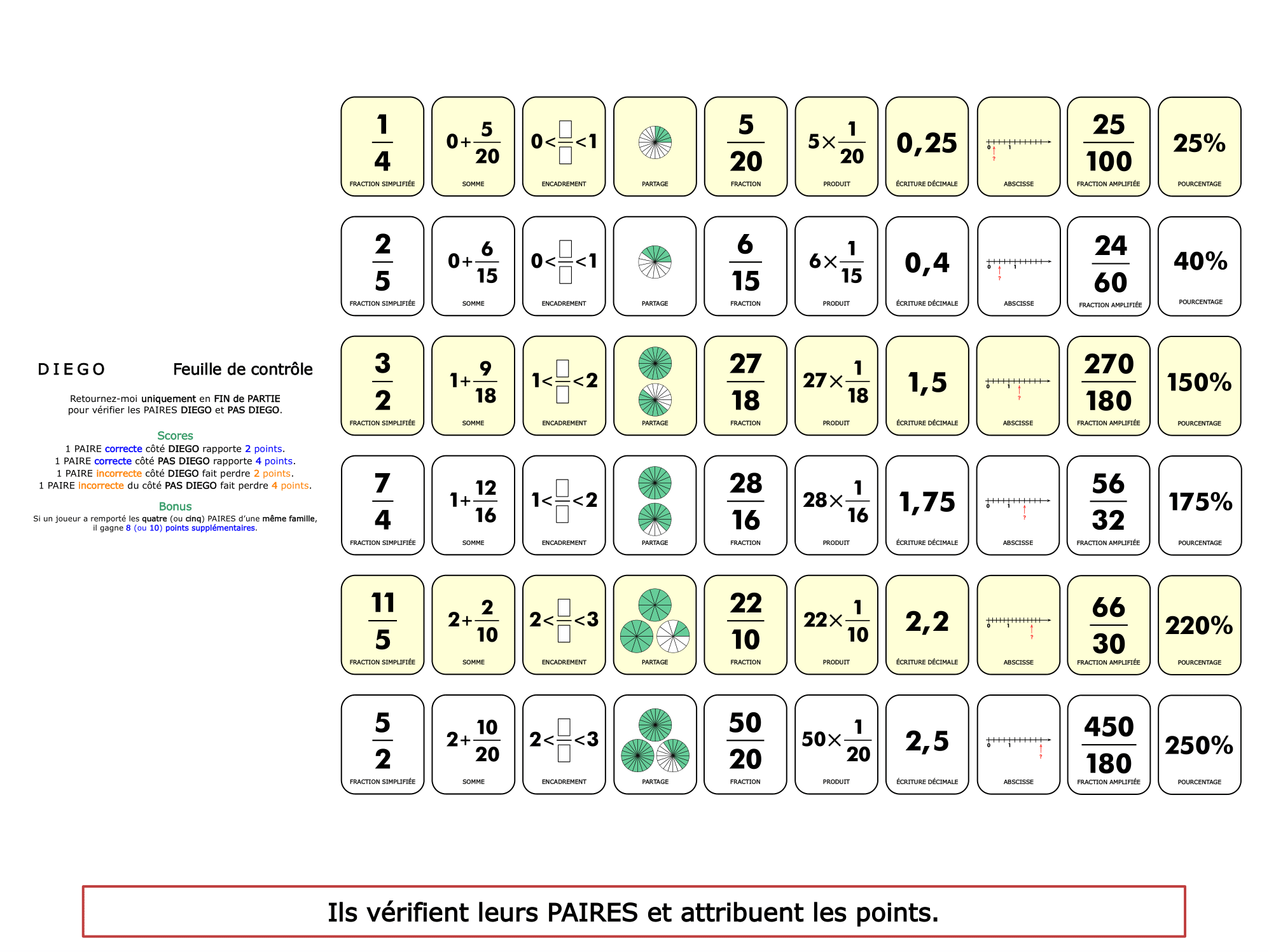
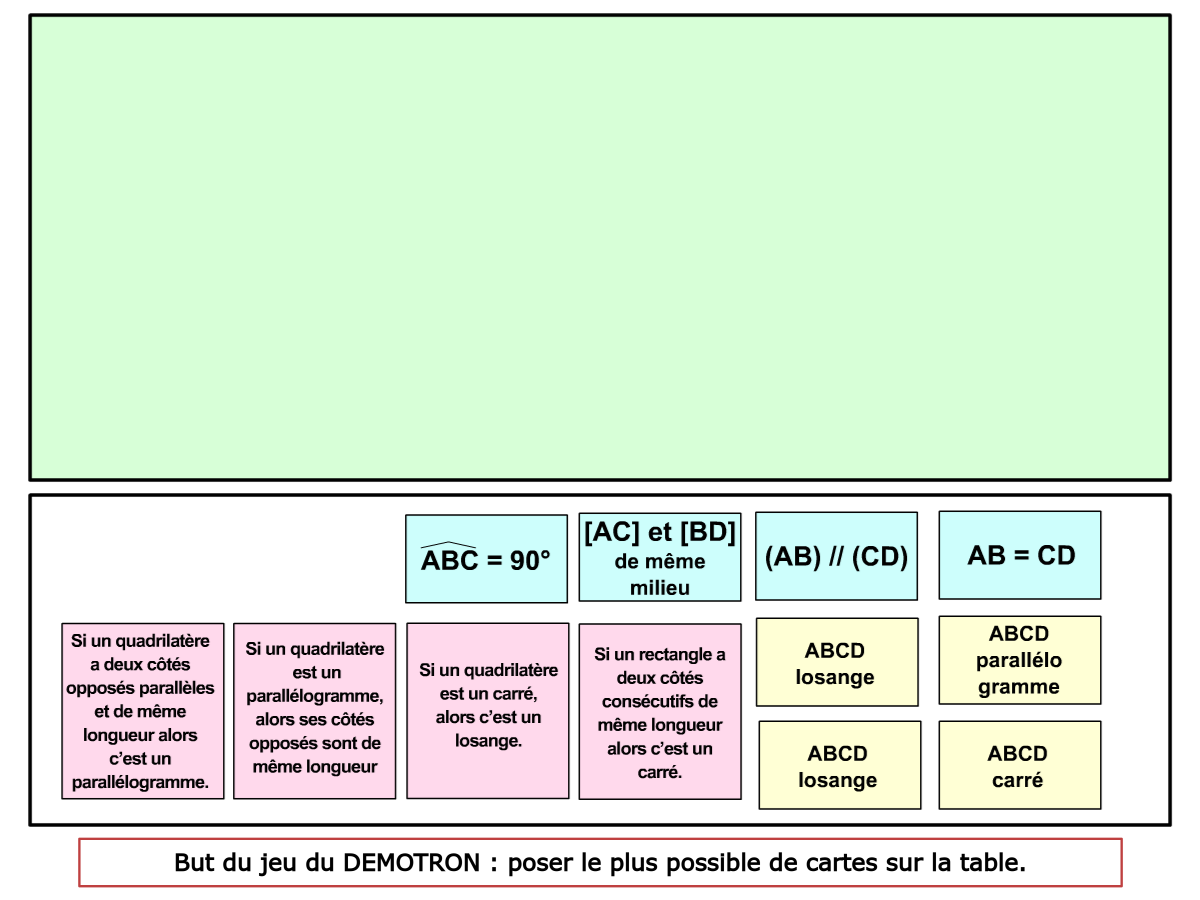
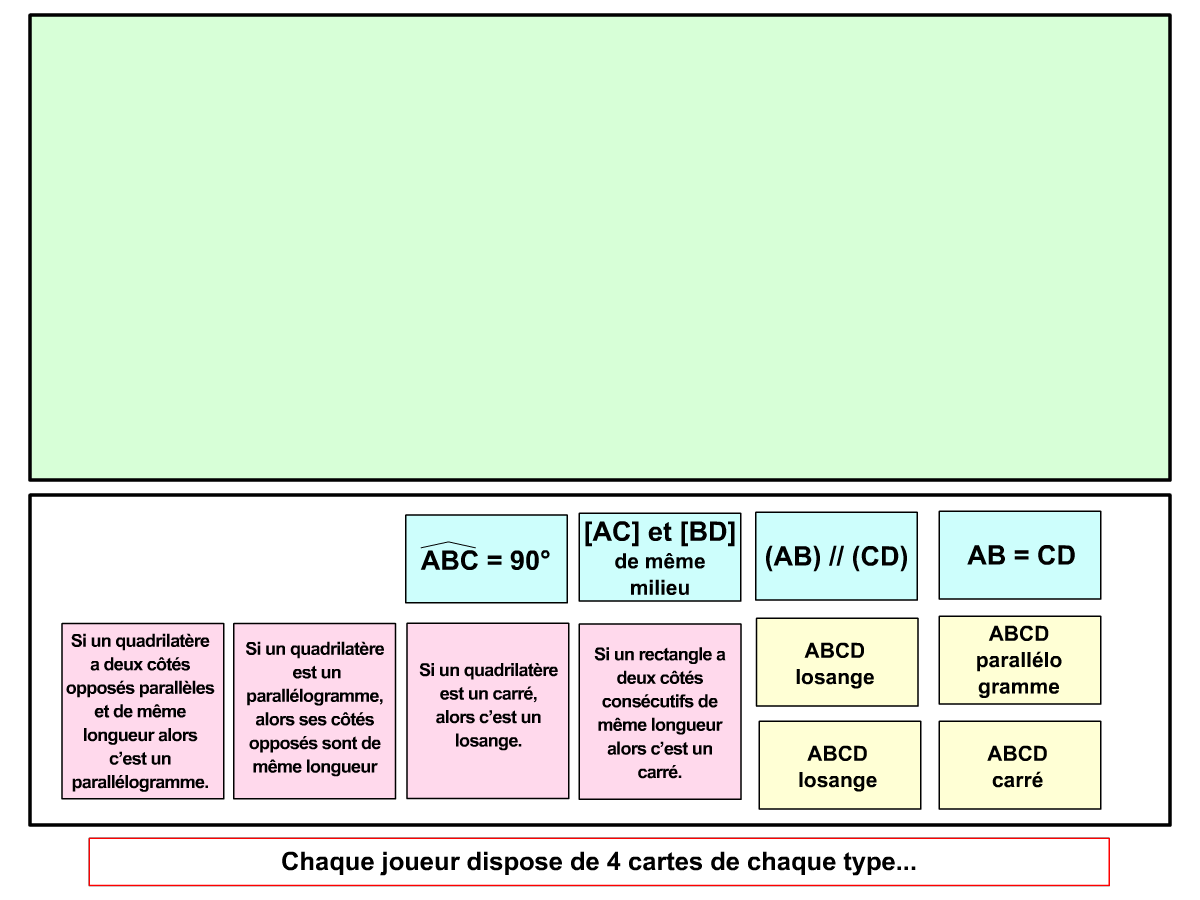
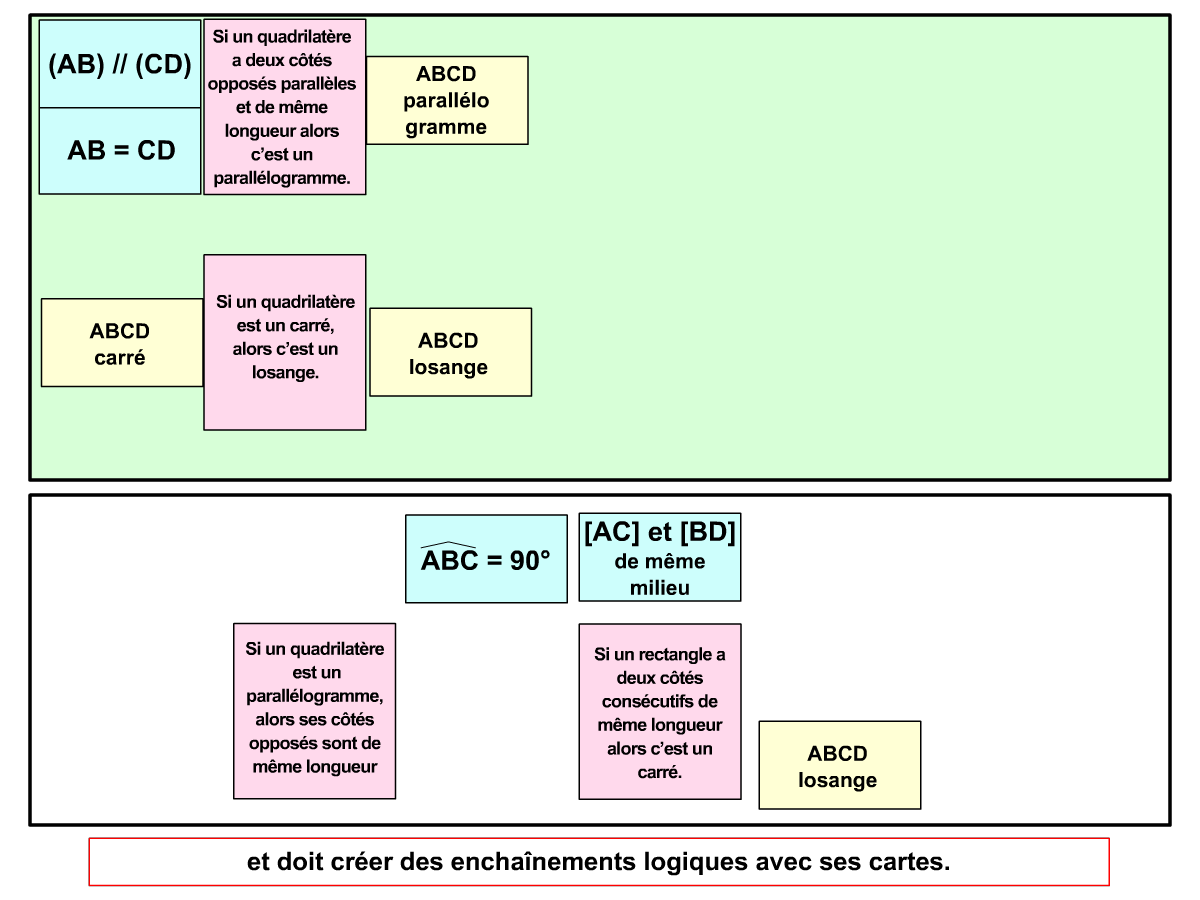
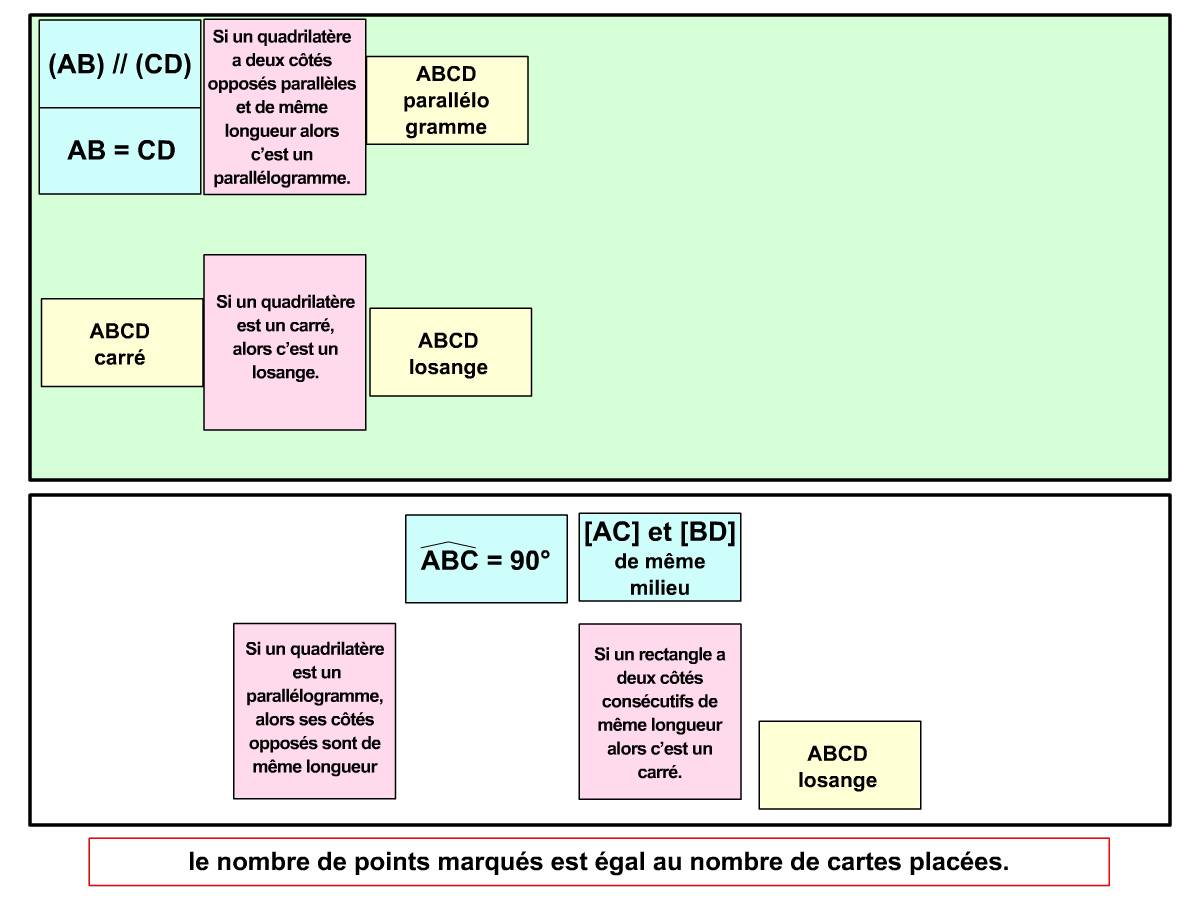
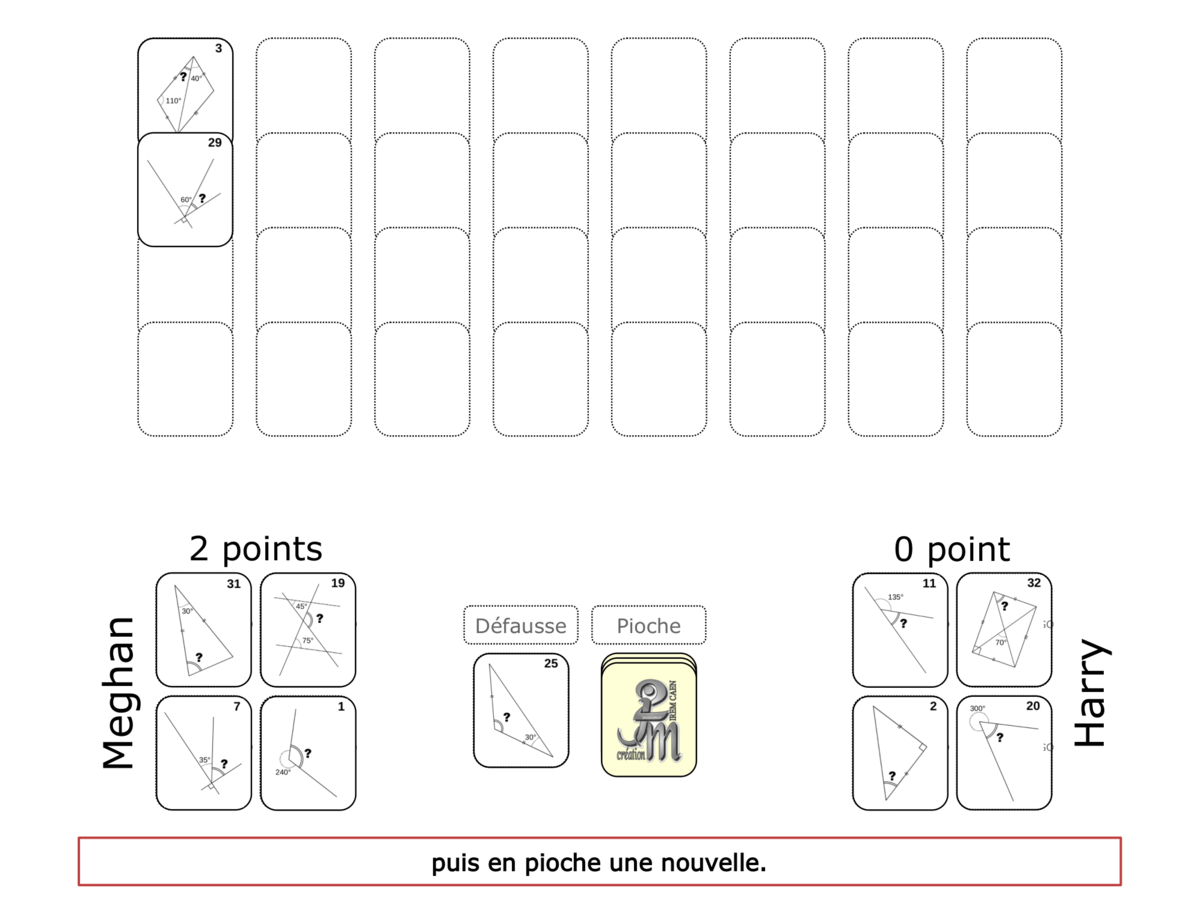
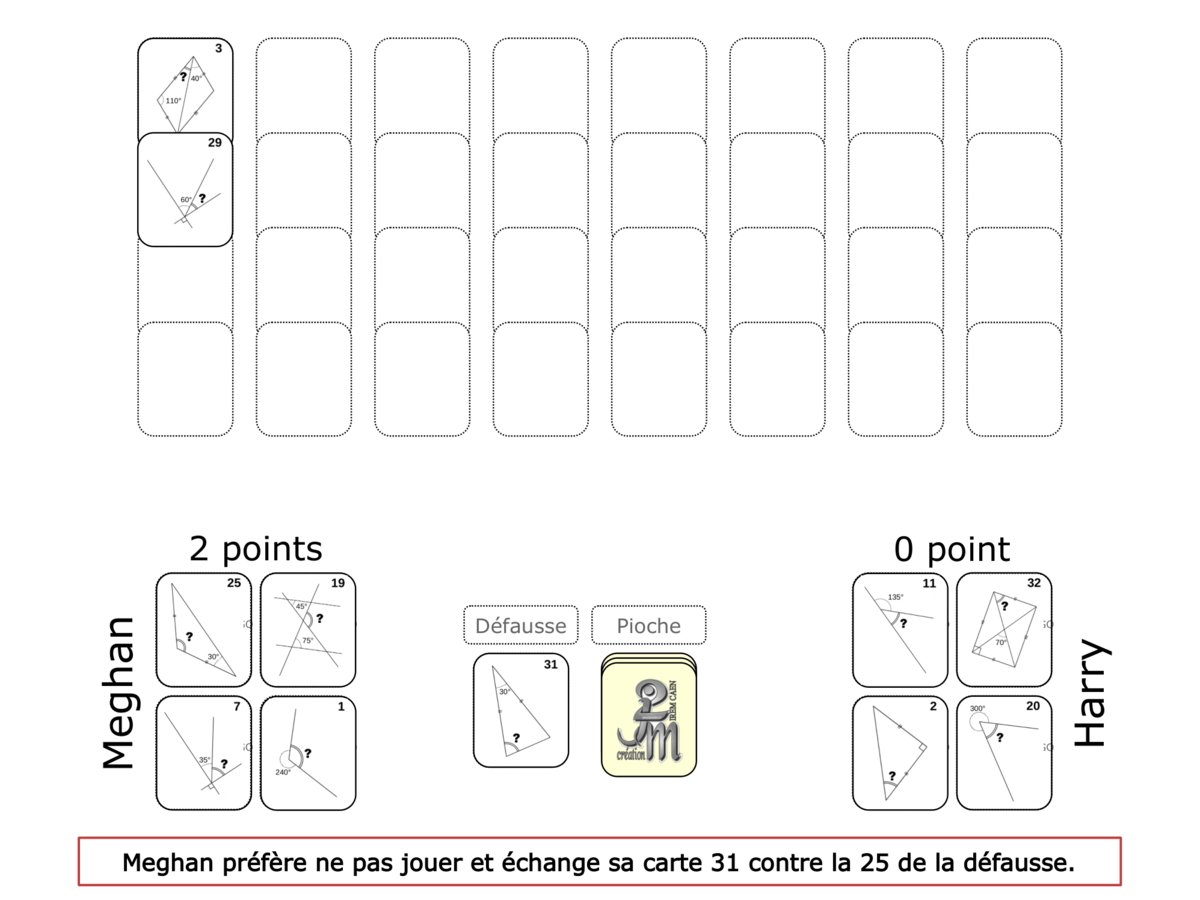
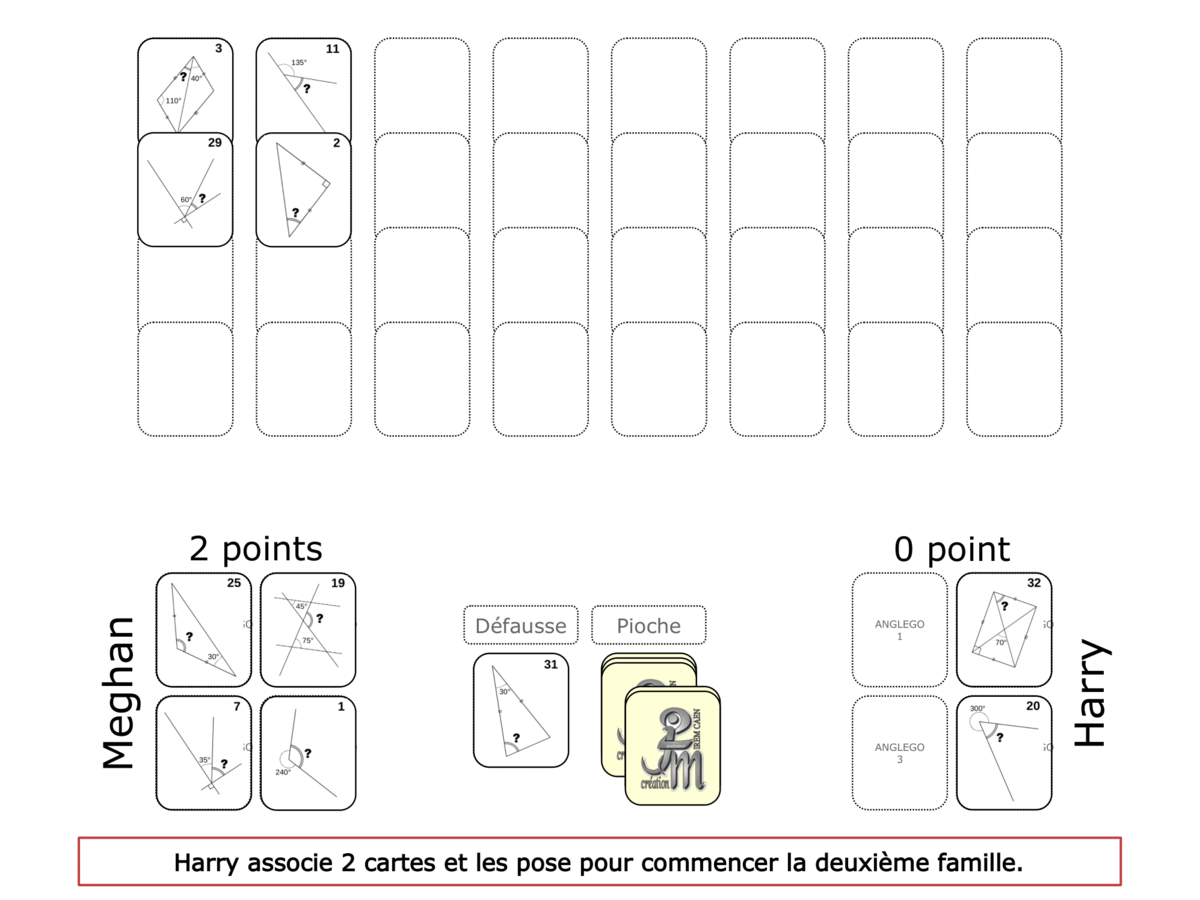
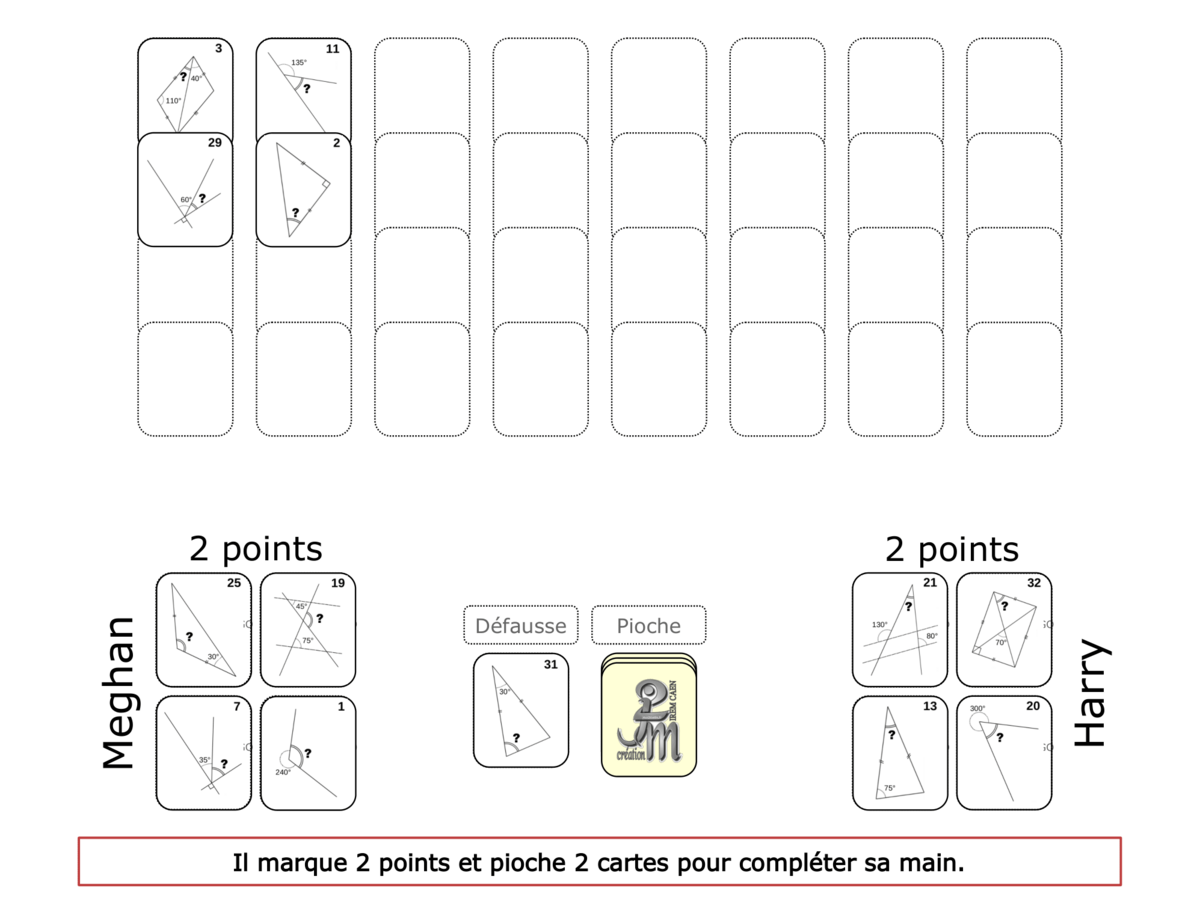
La démo
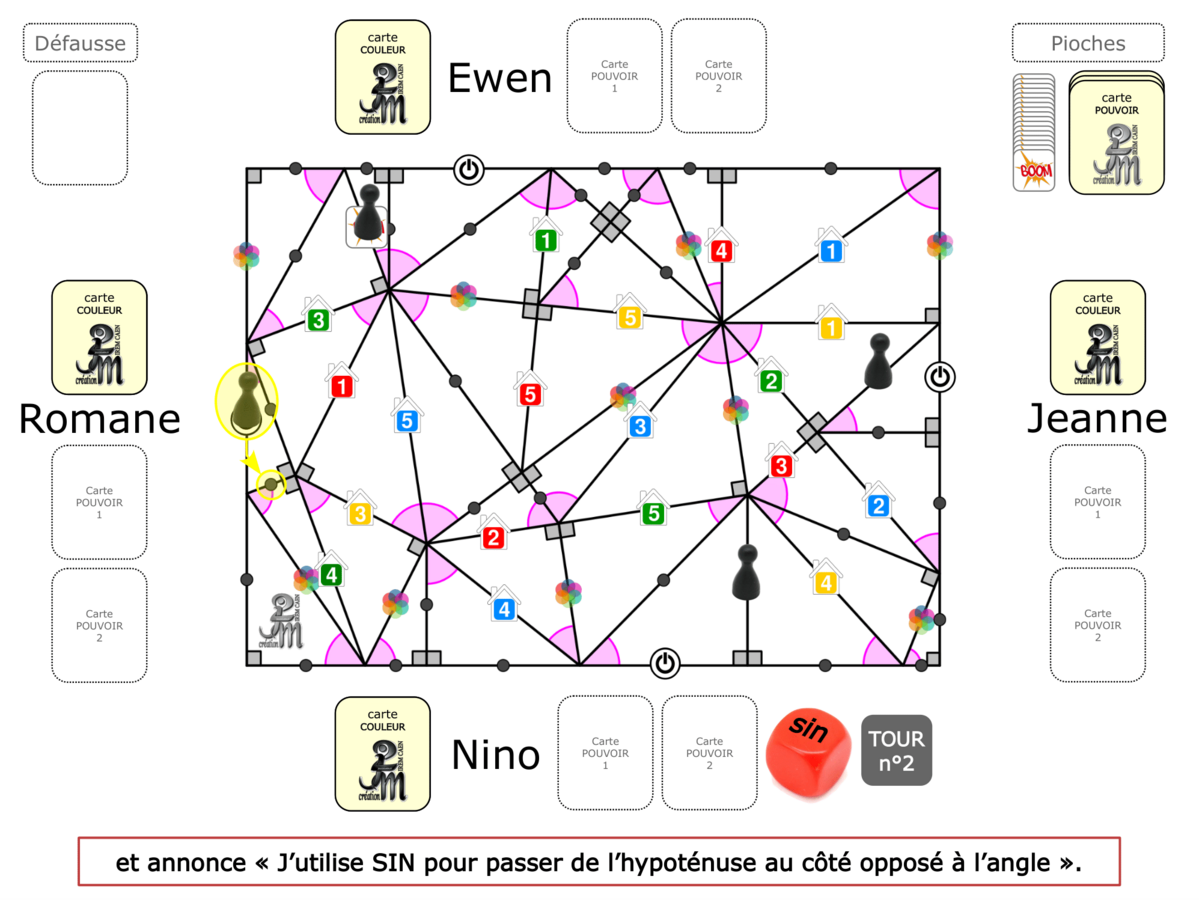
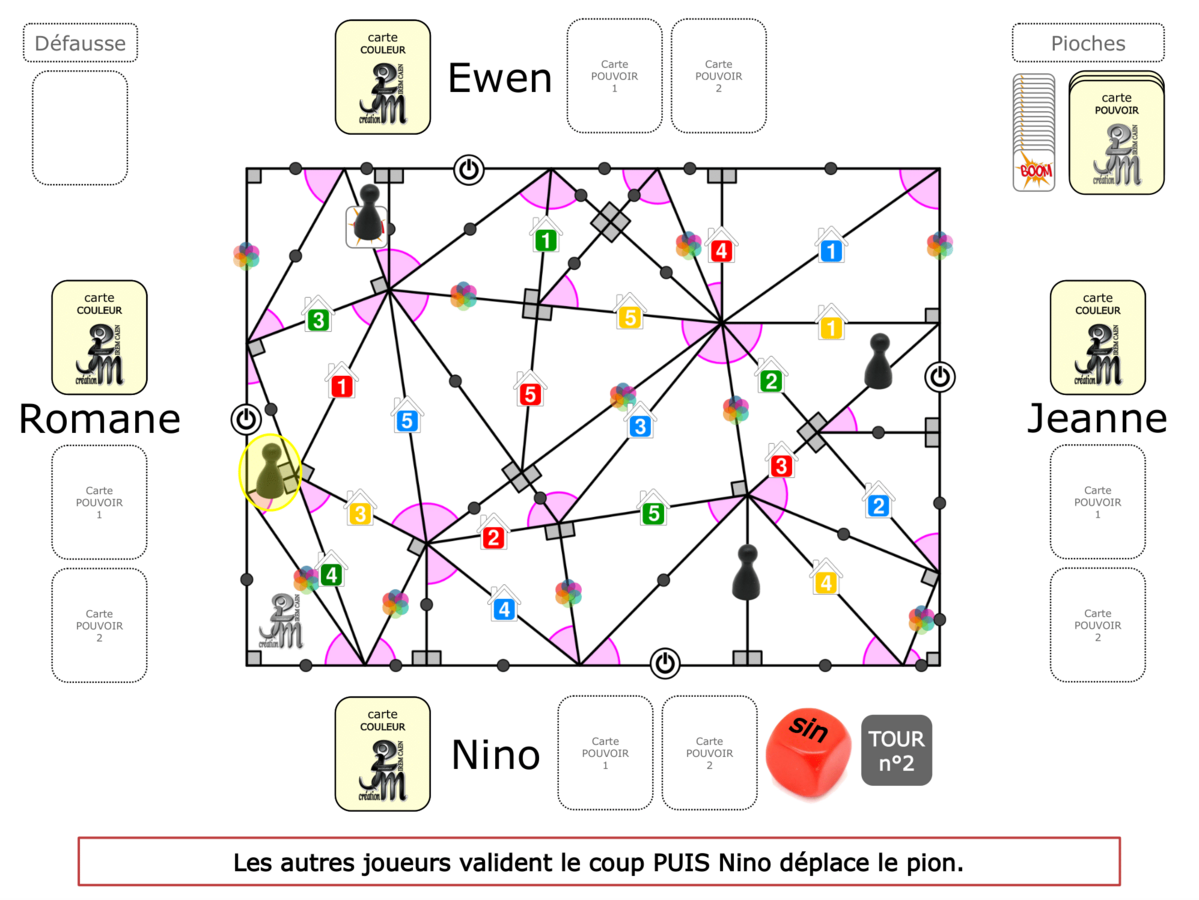
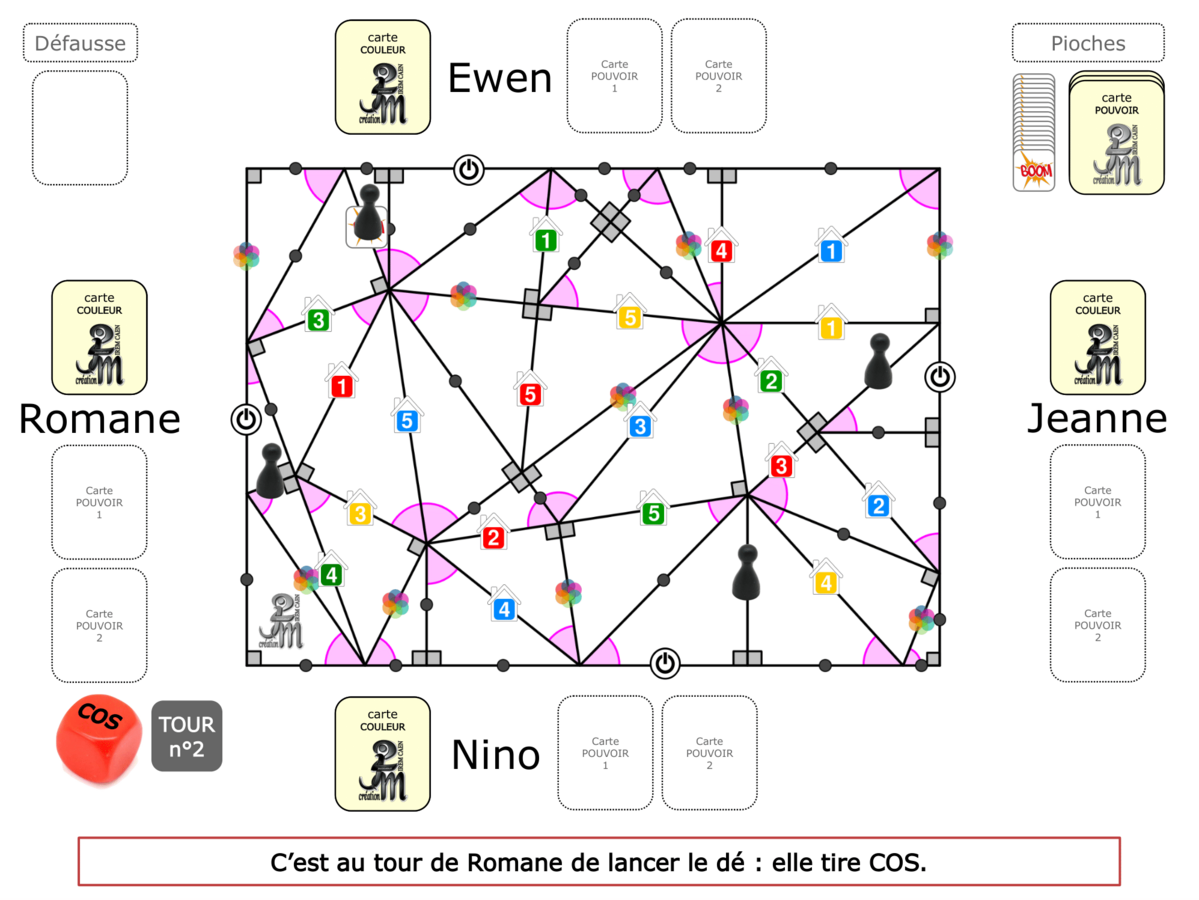
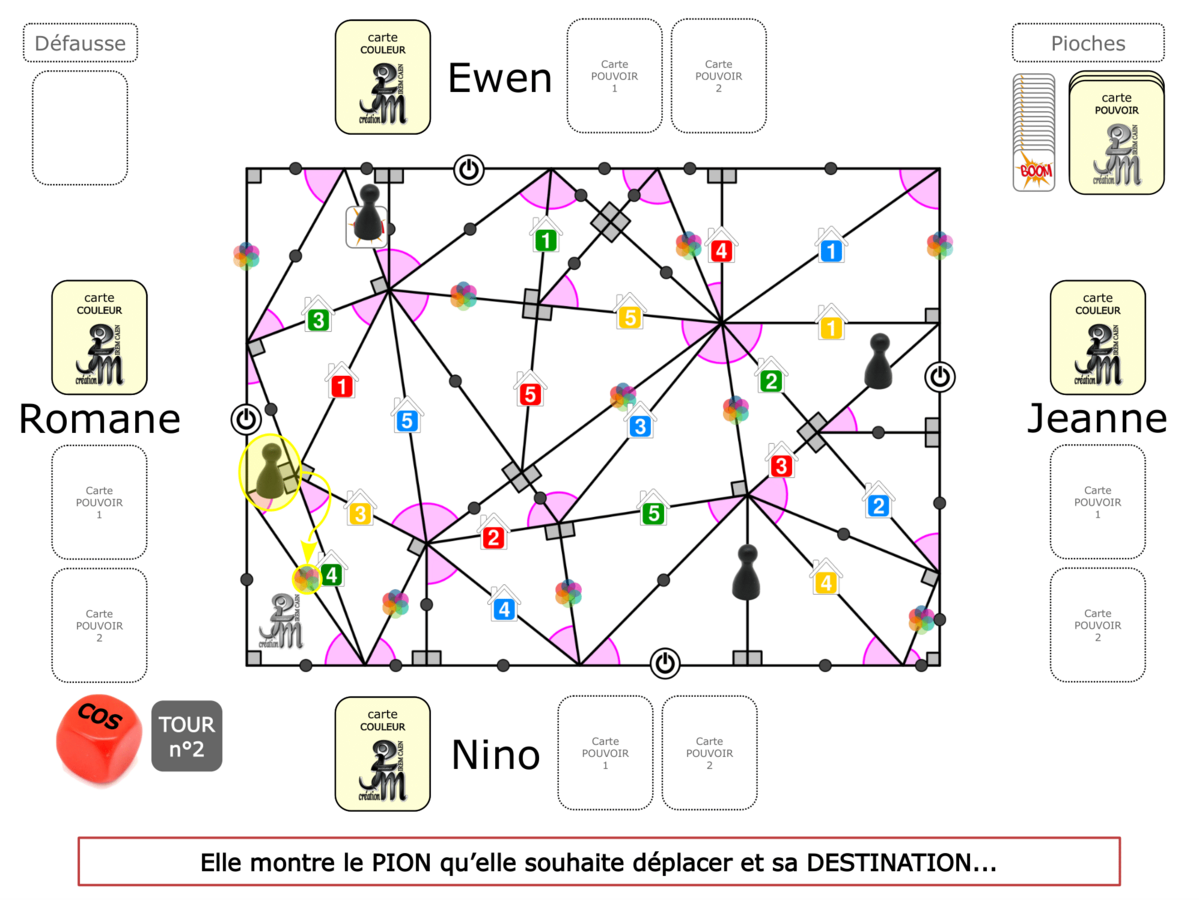
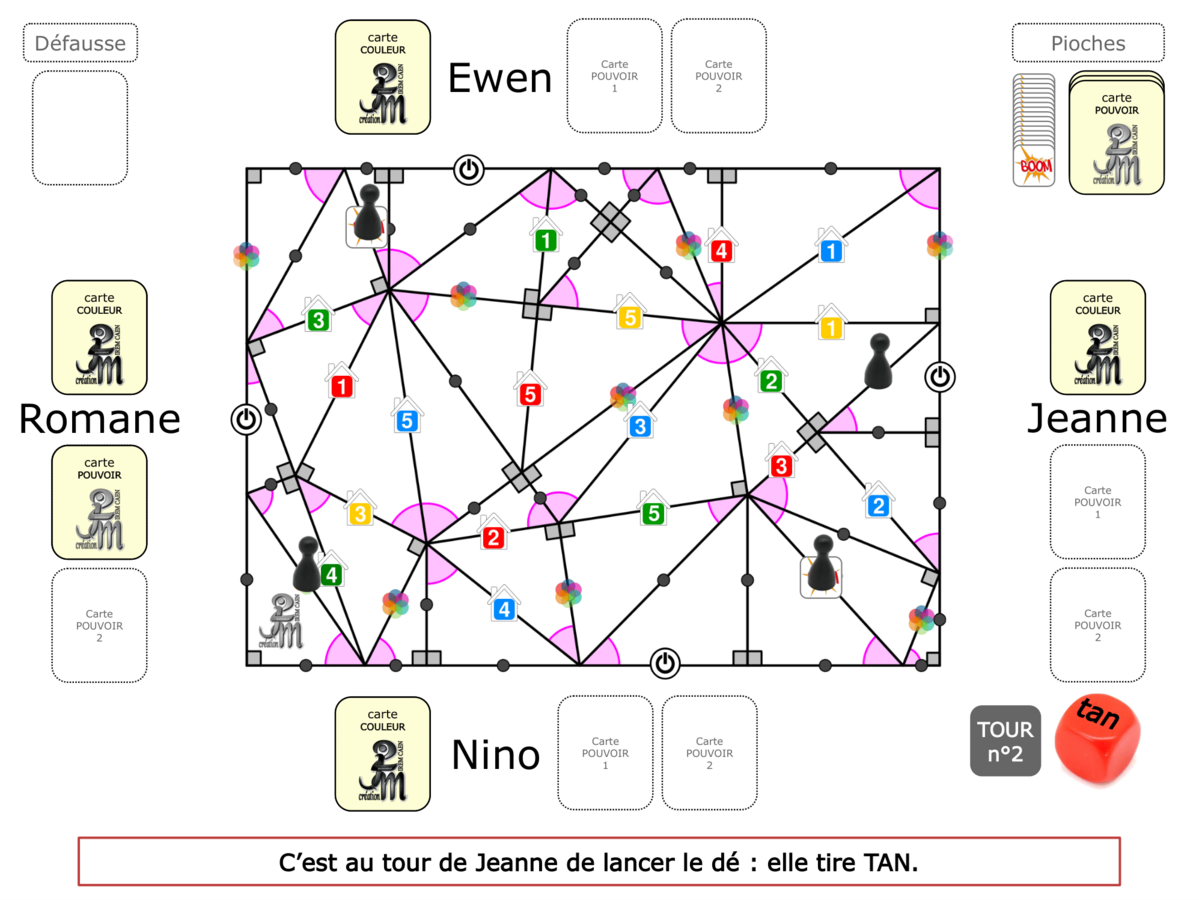
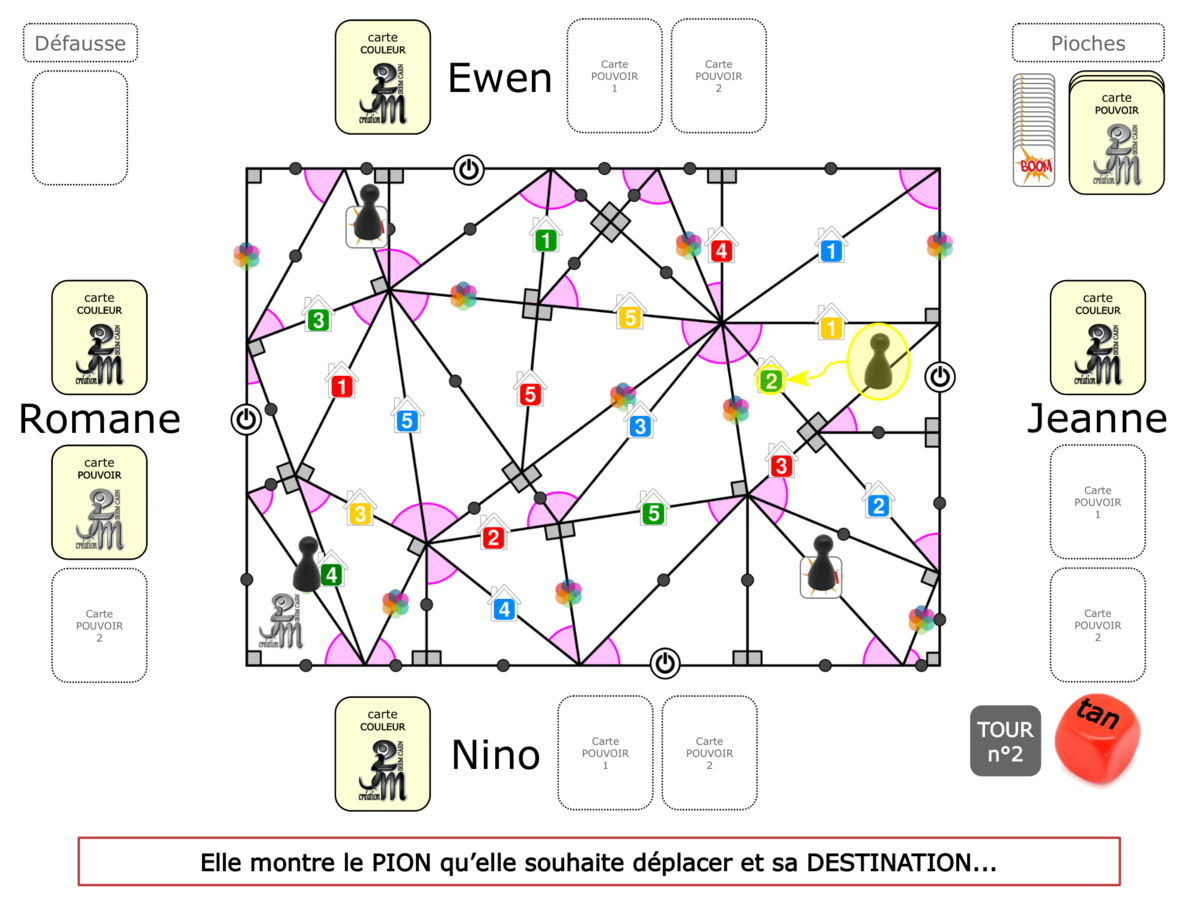
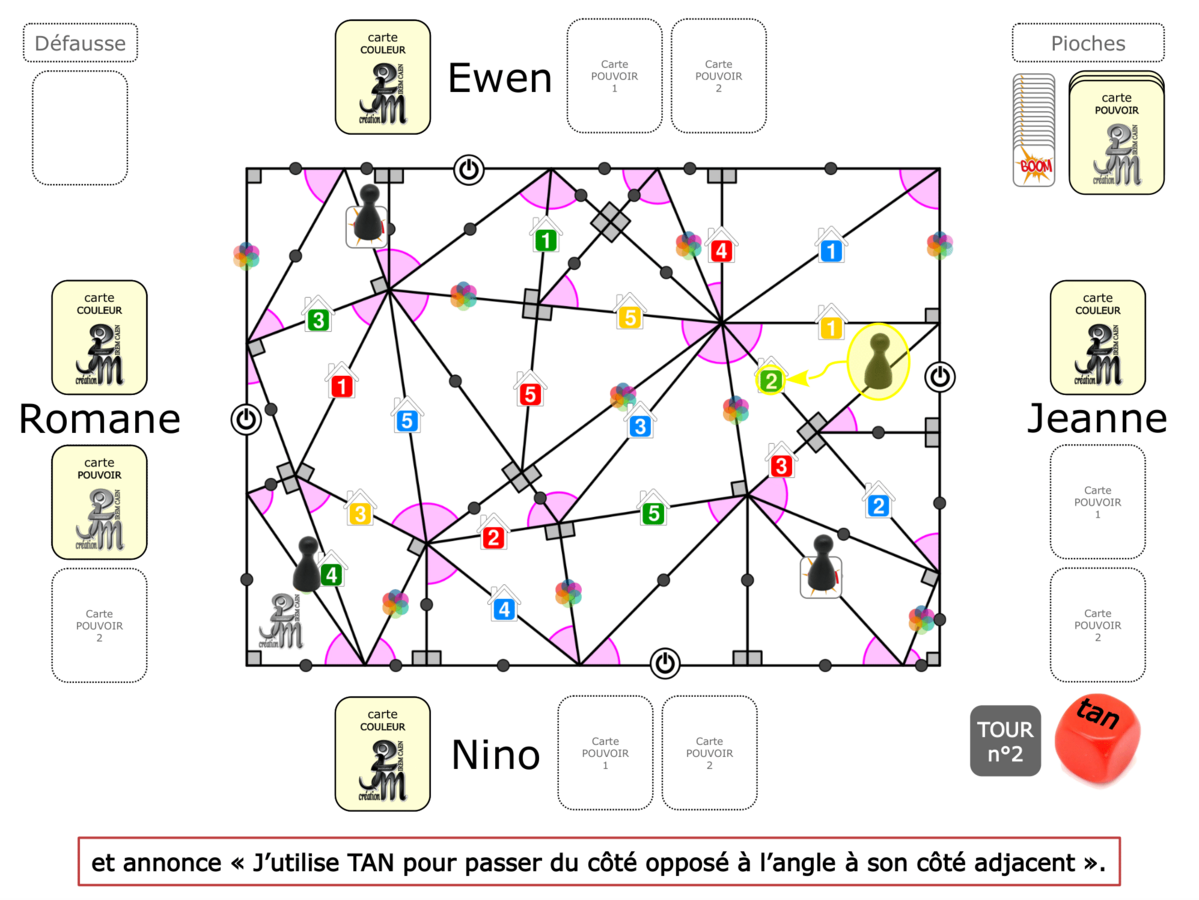
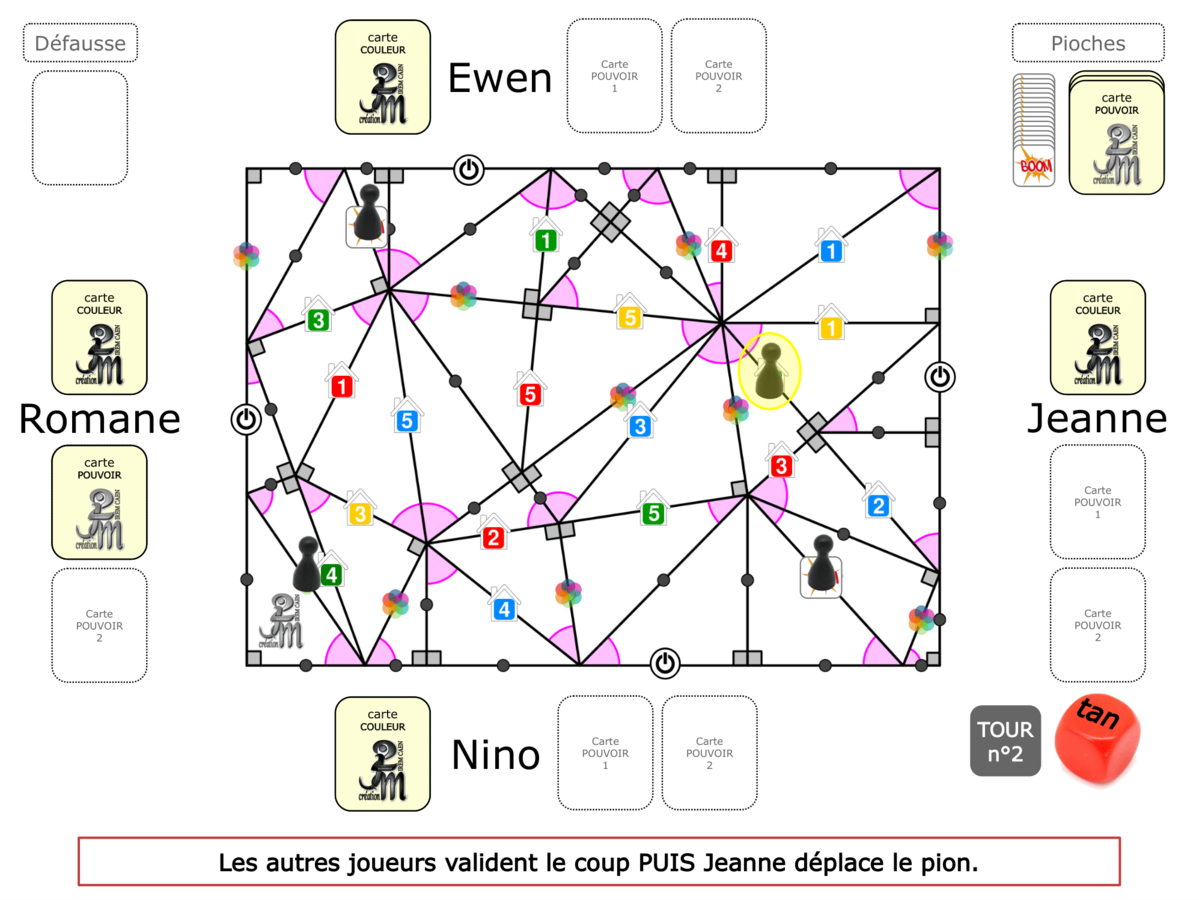
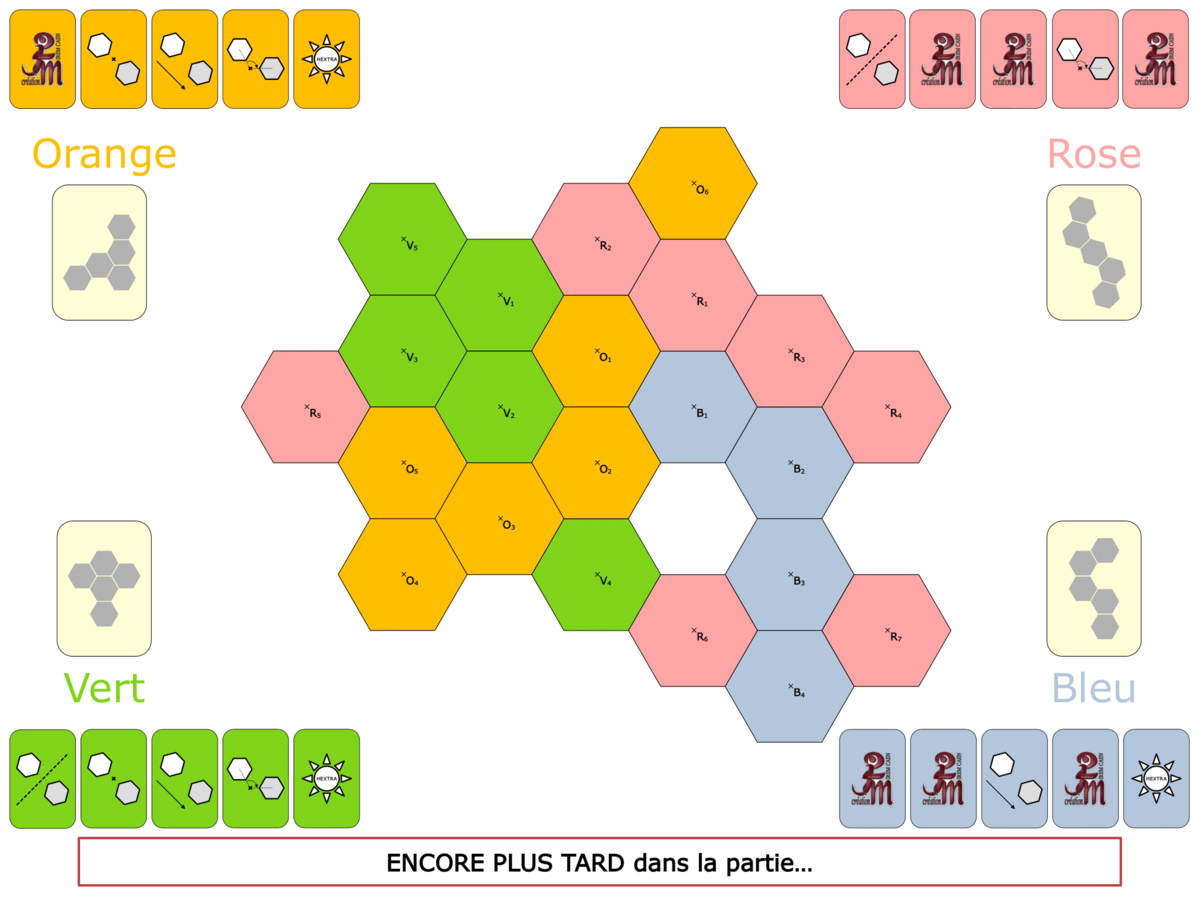
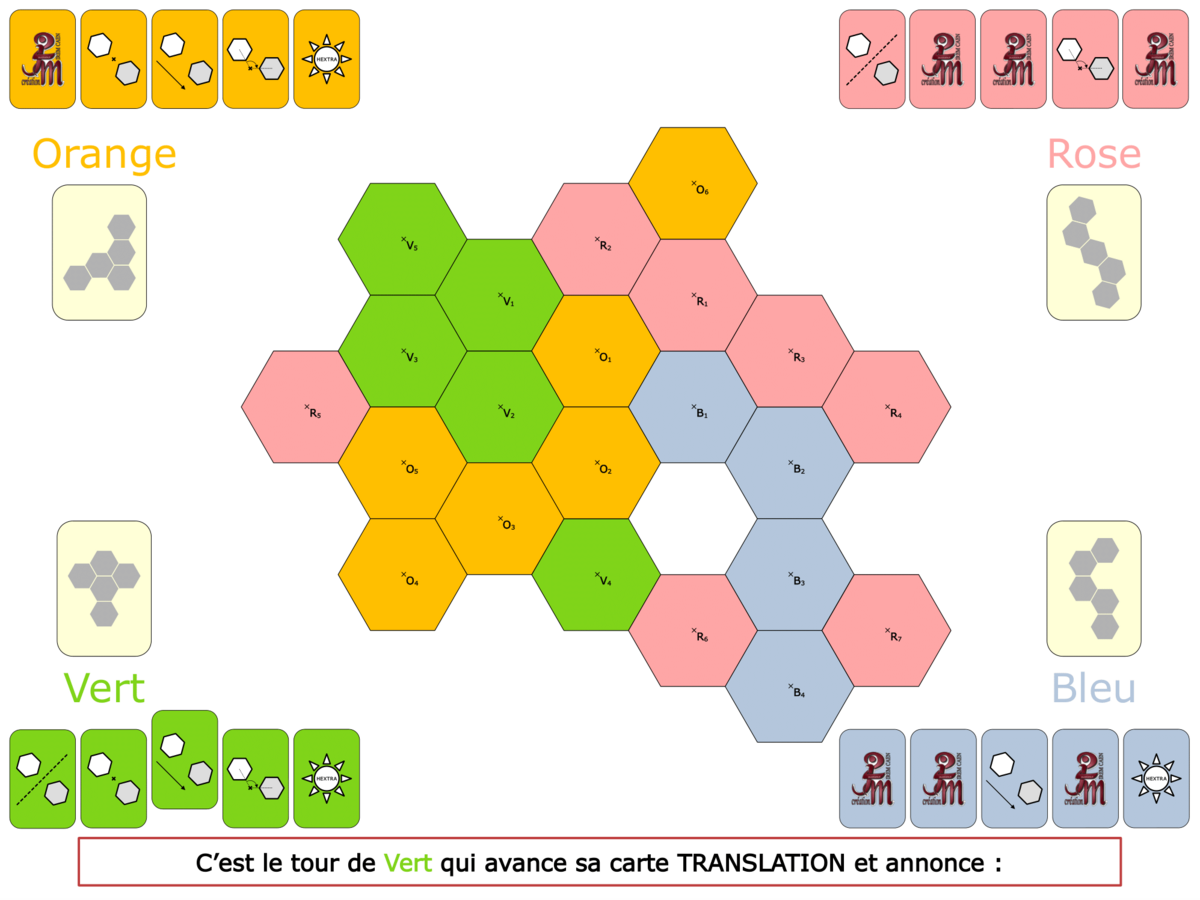
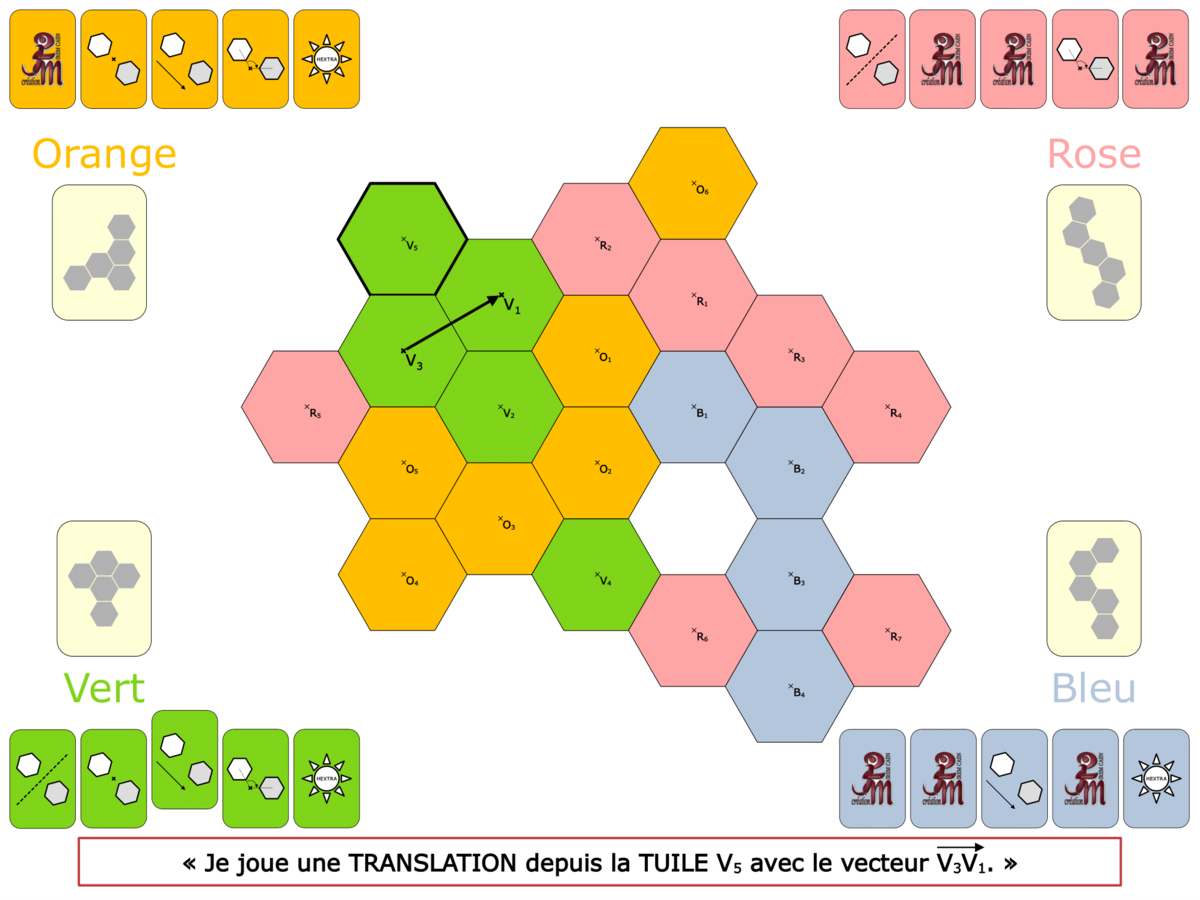
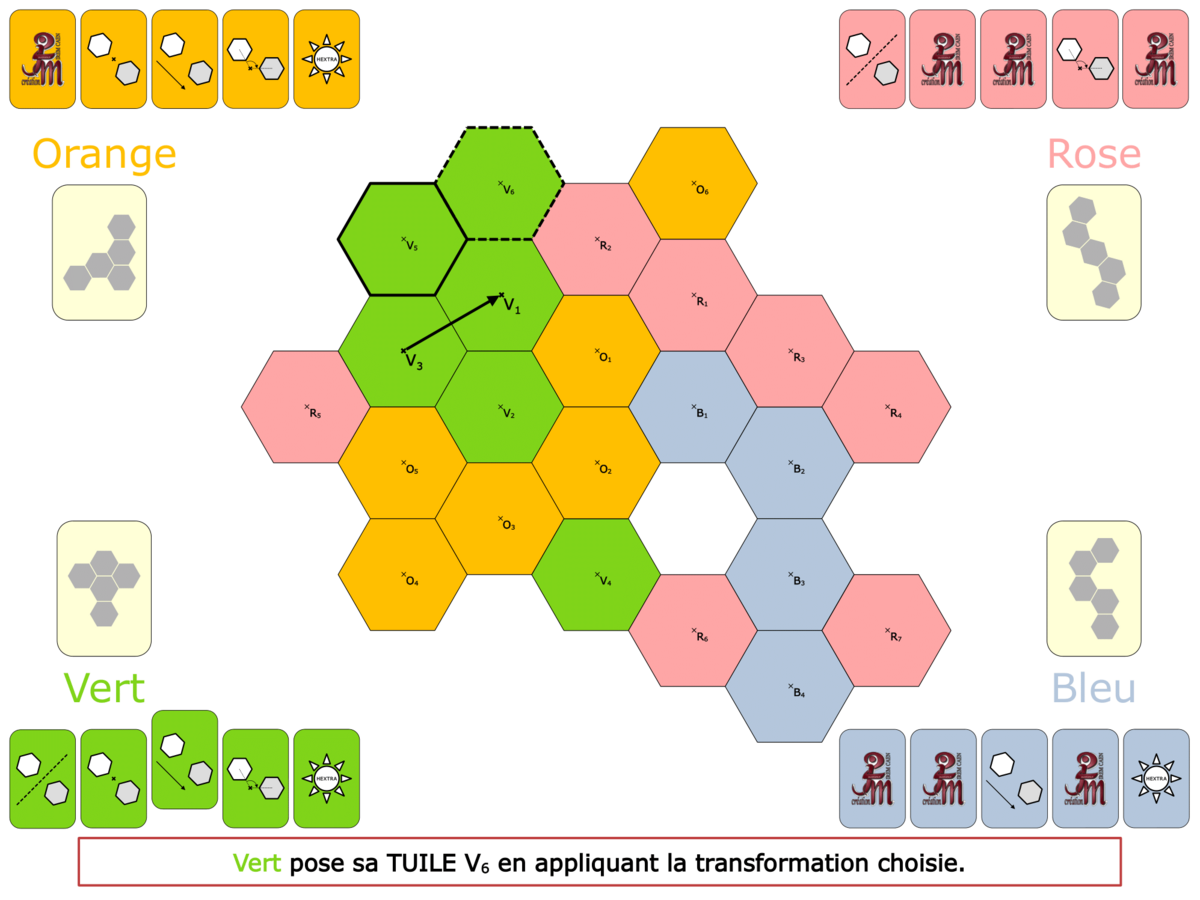
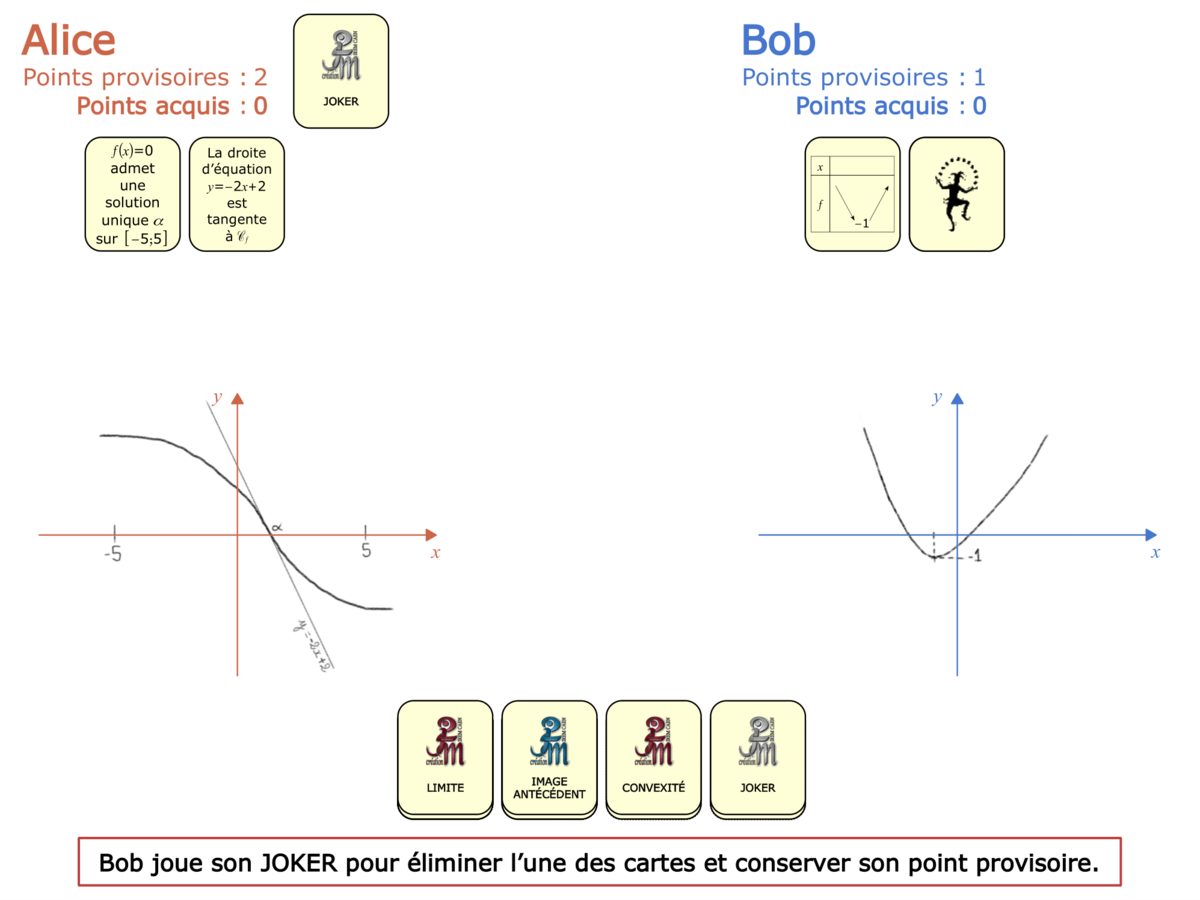
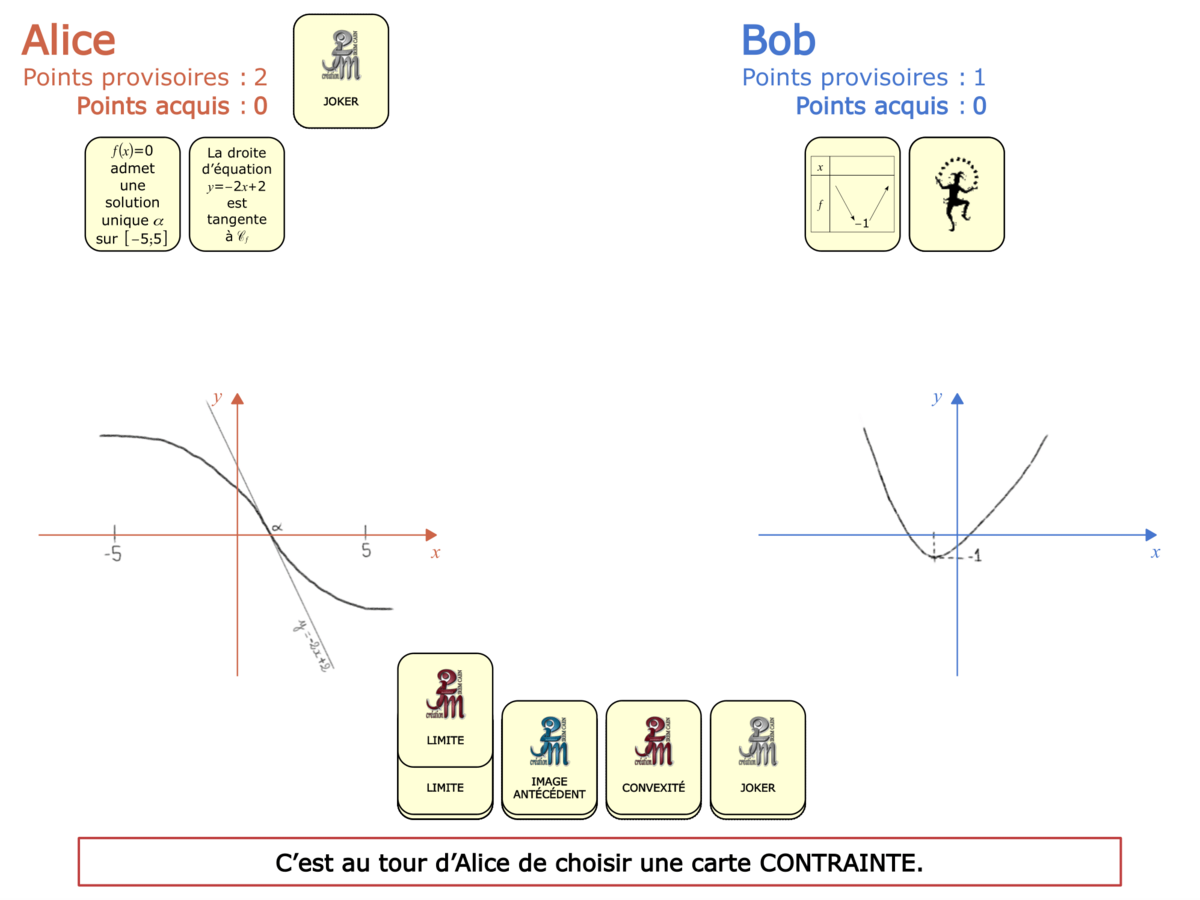
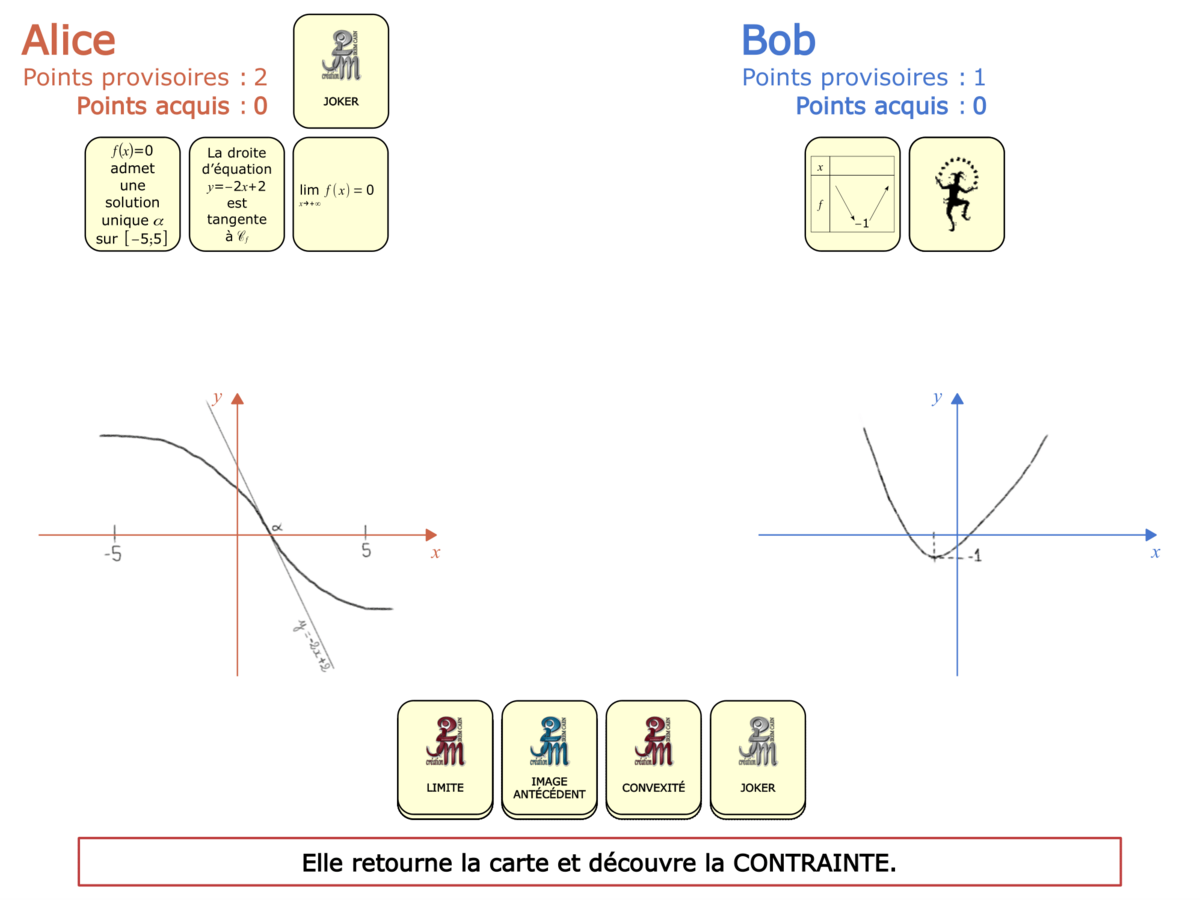
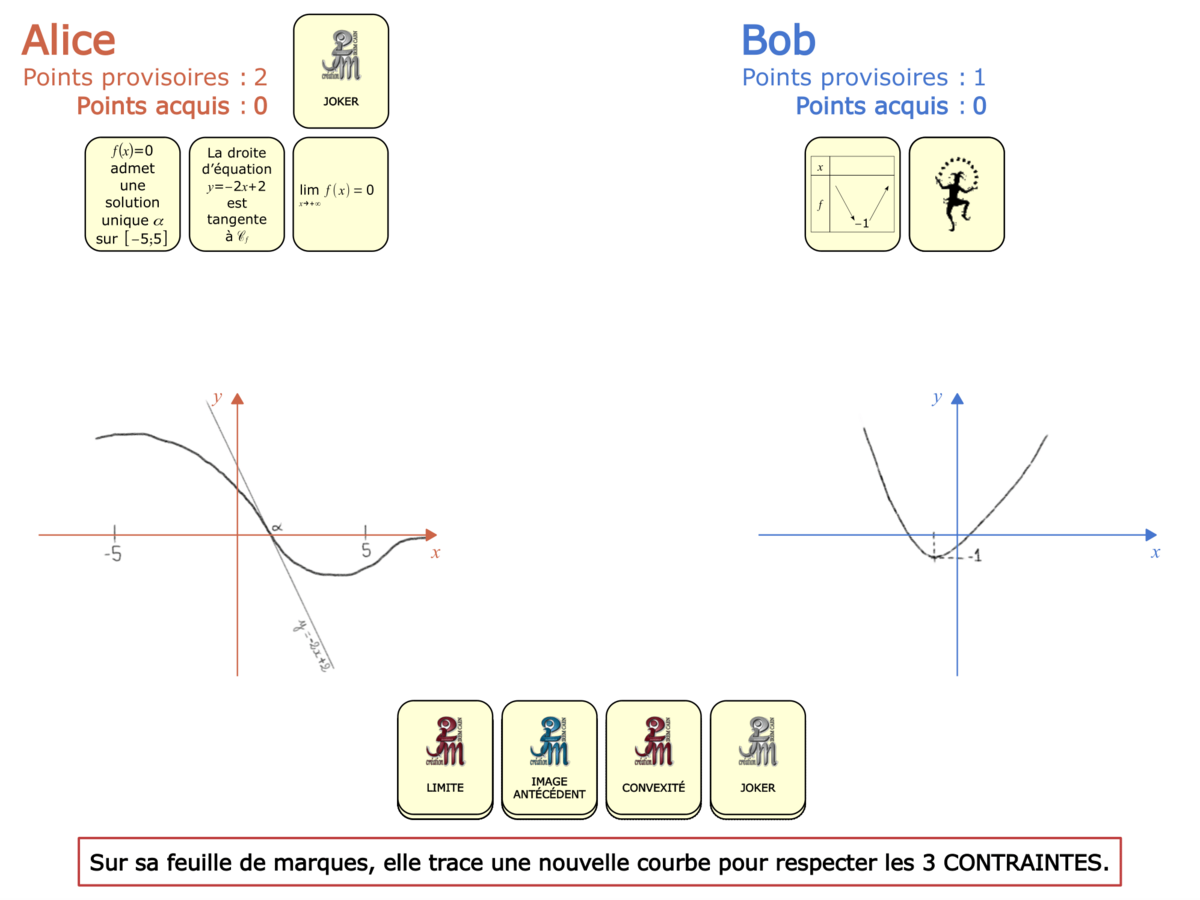
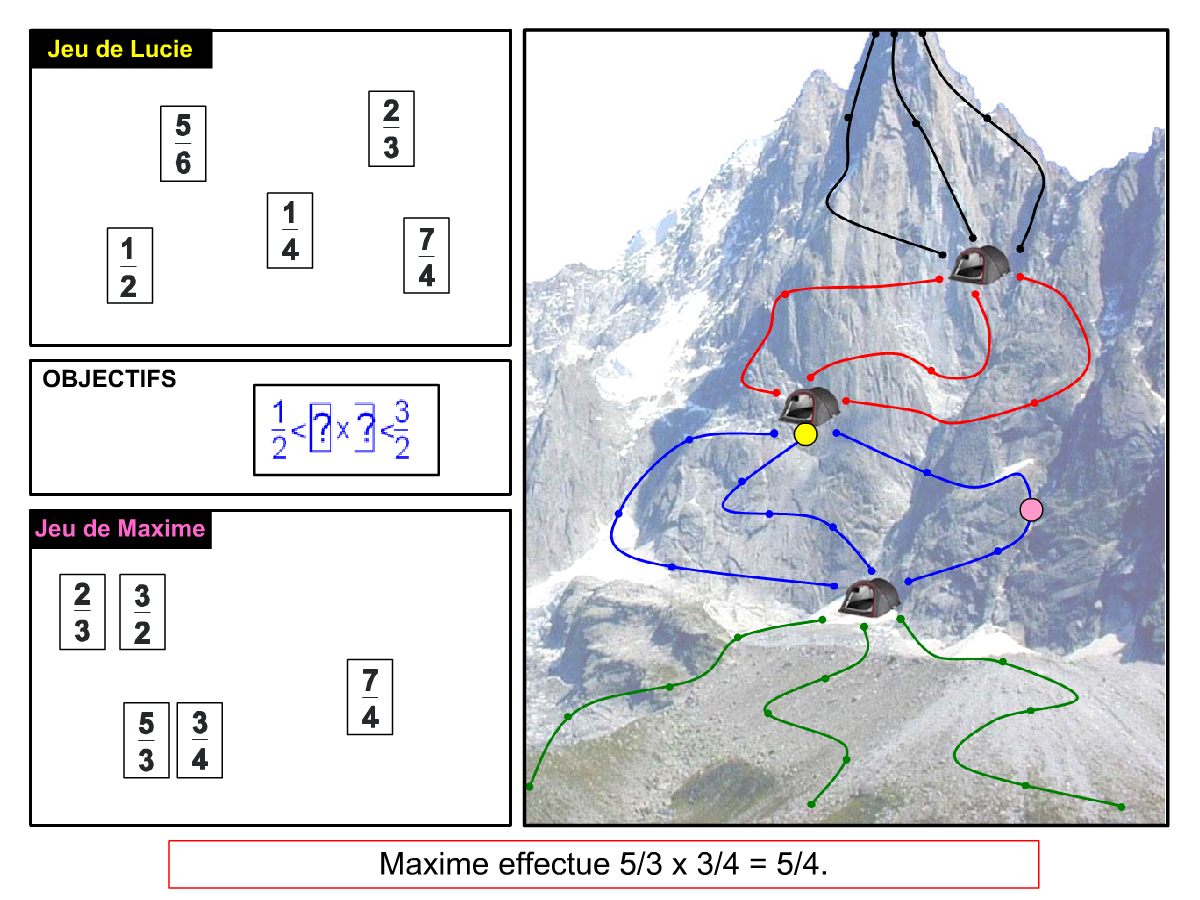
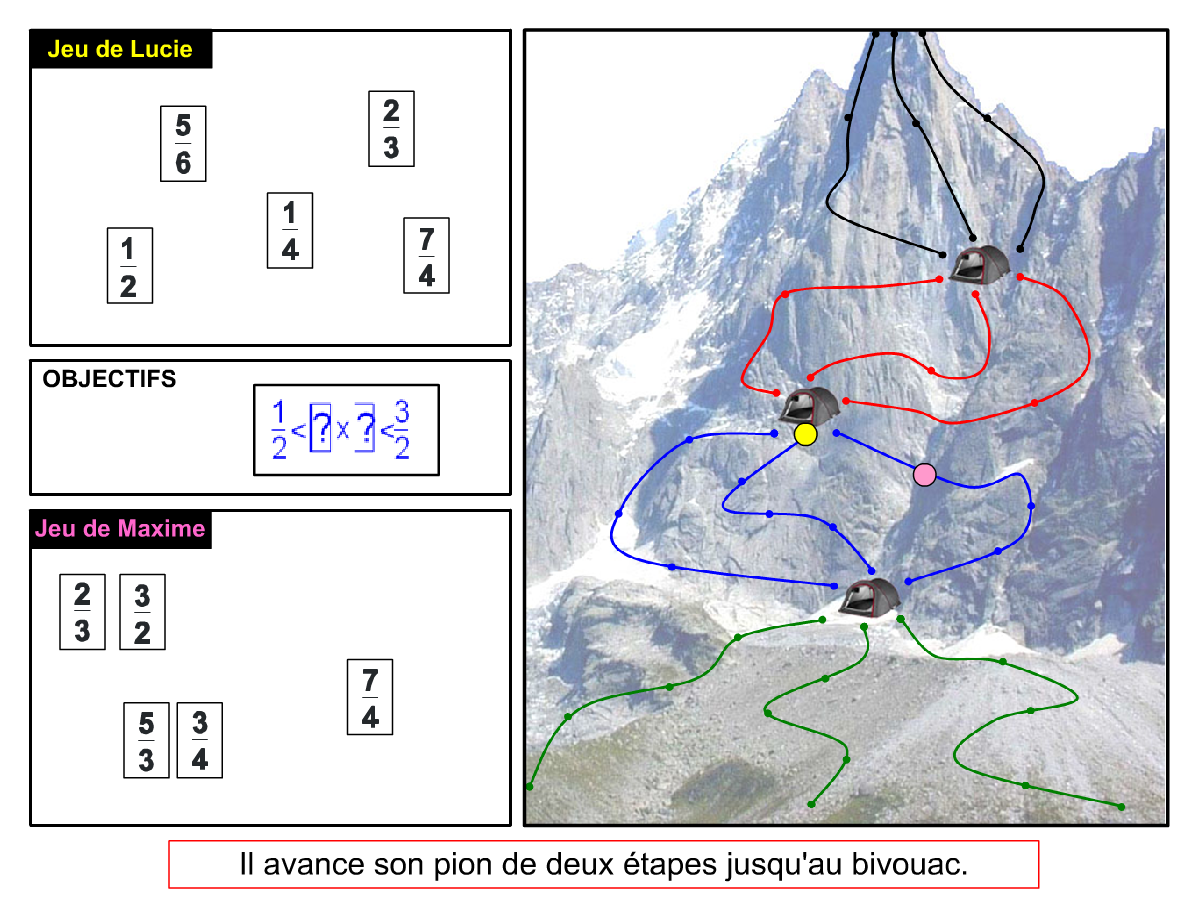
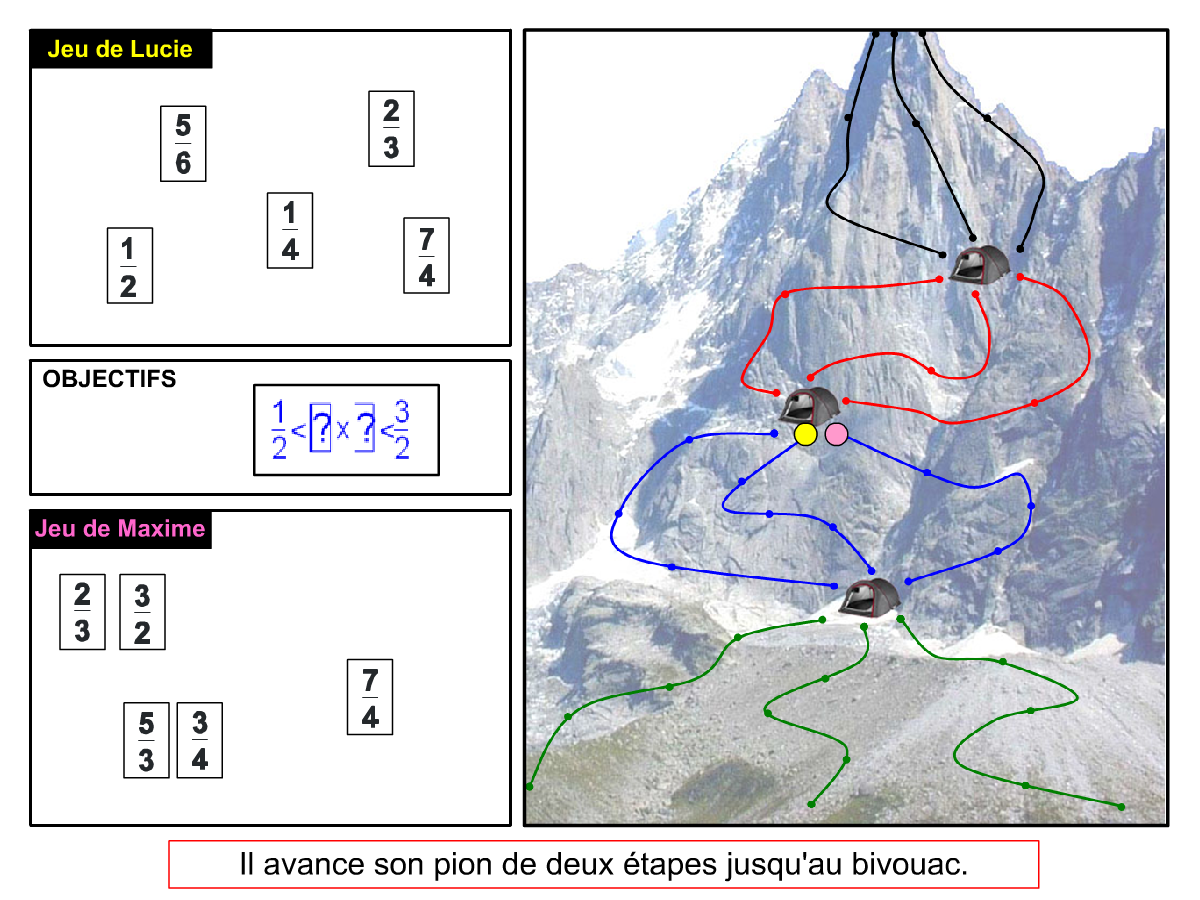
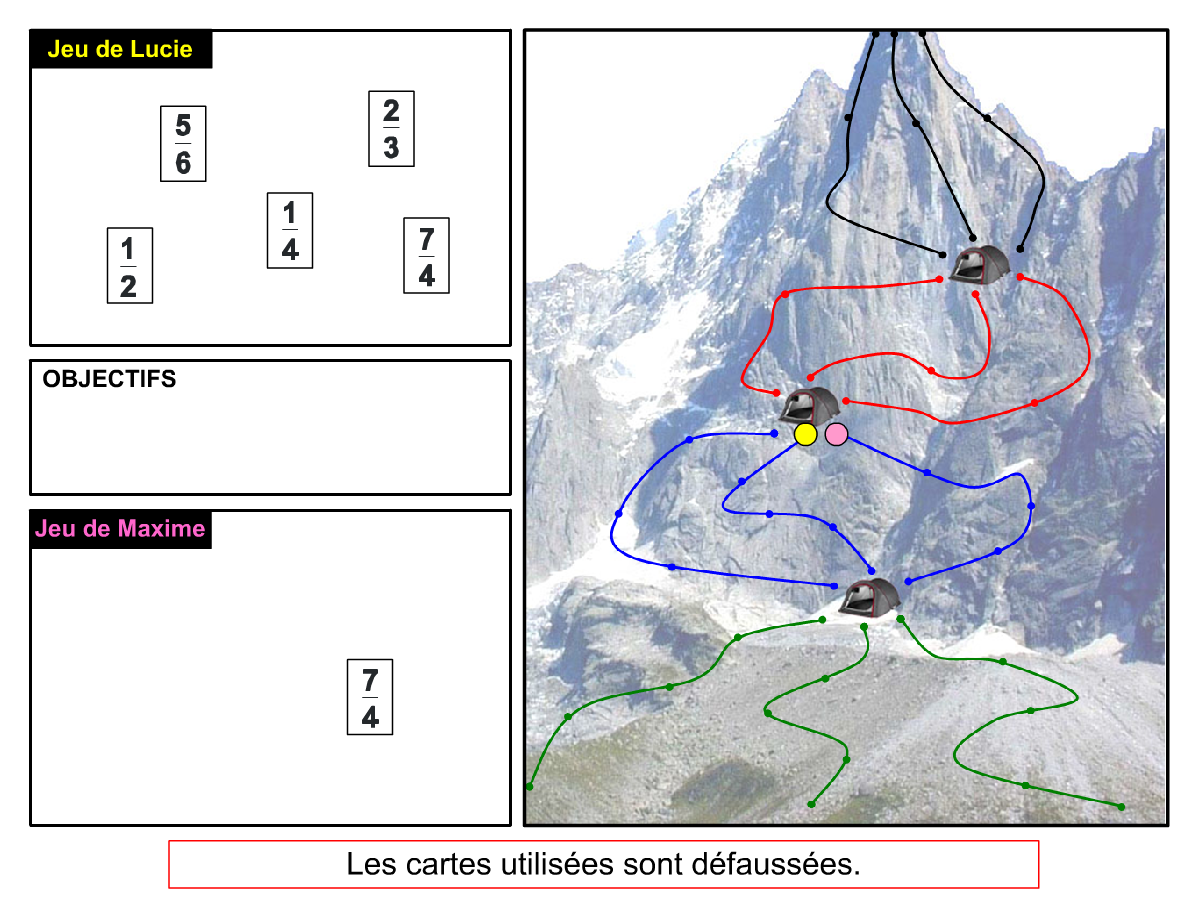
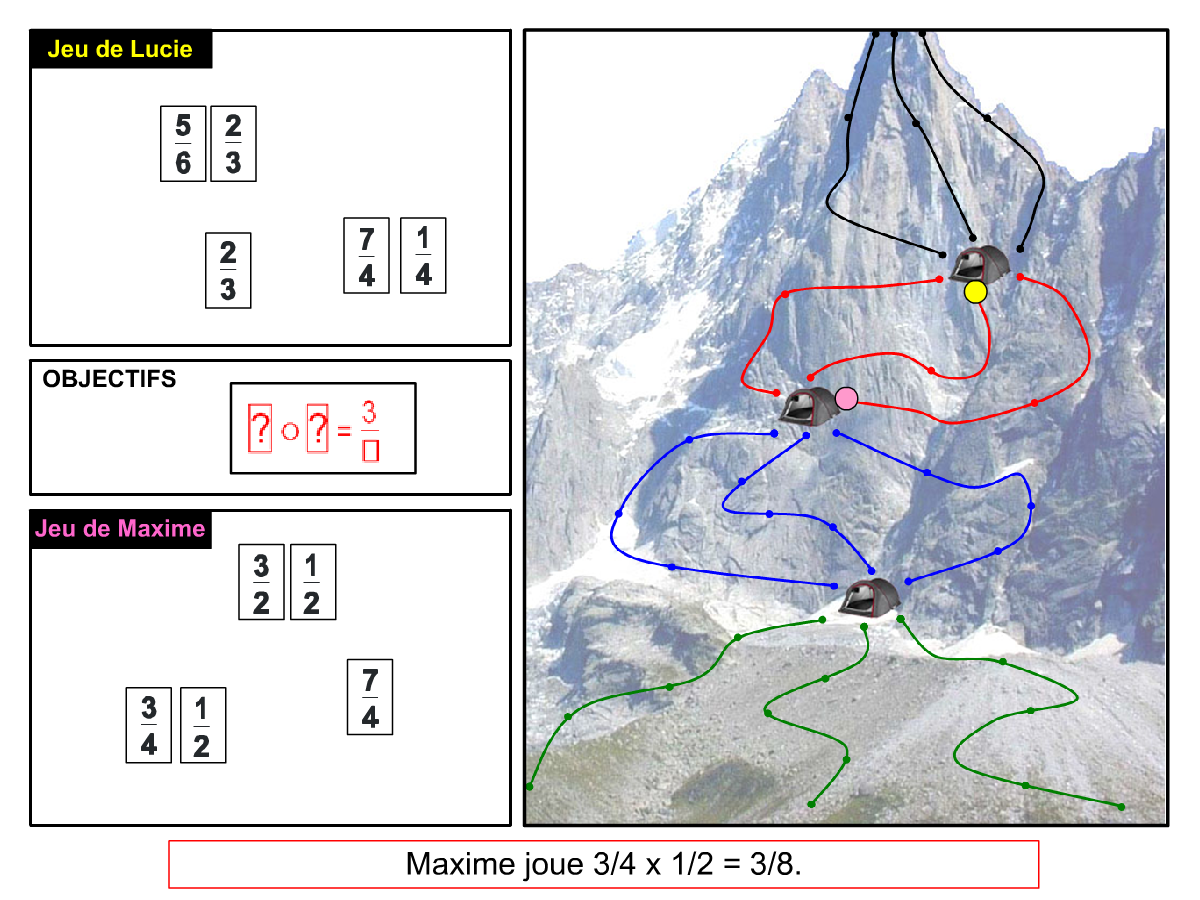
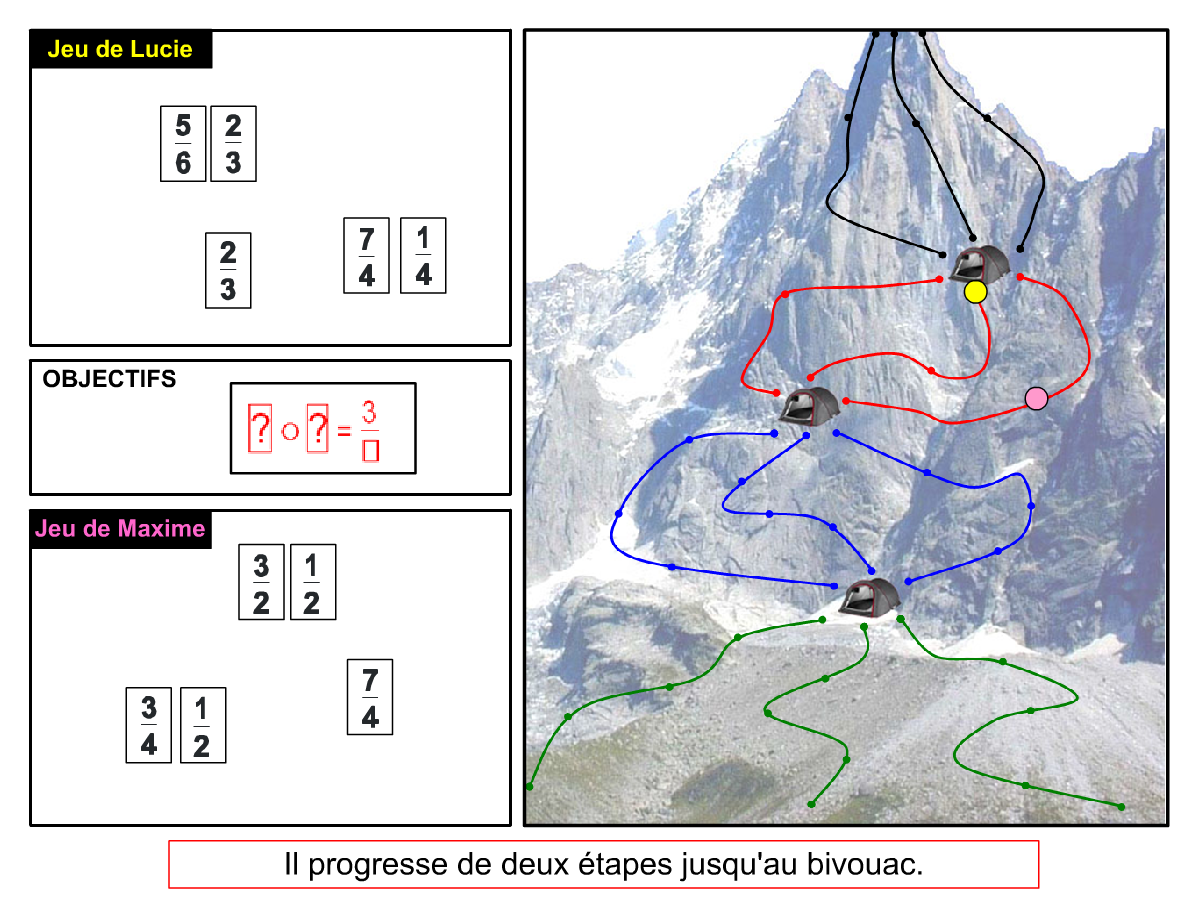
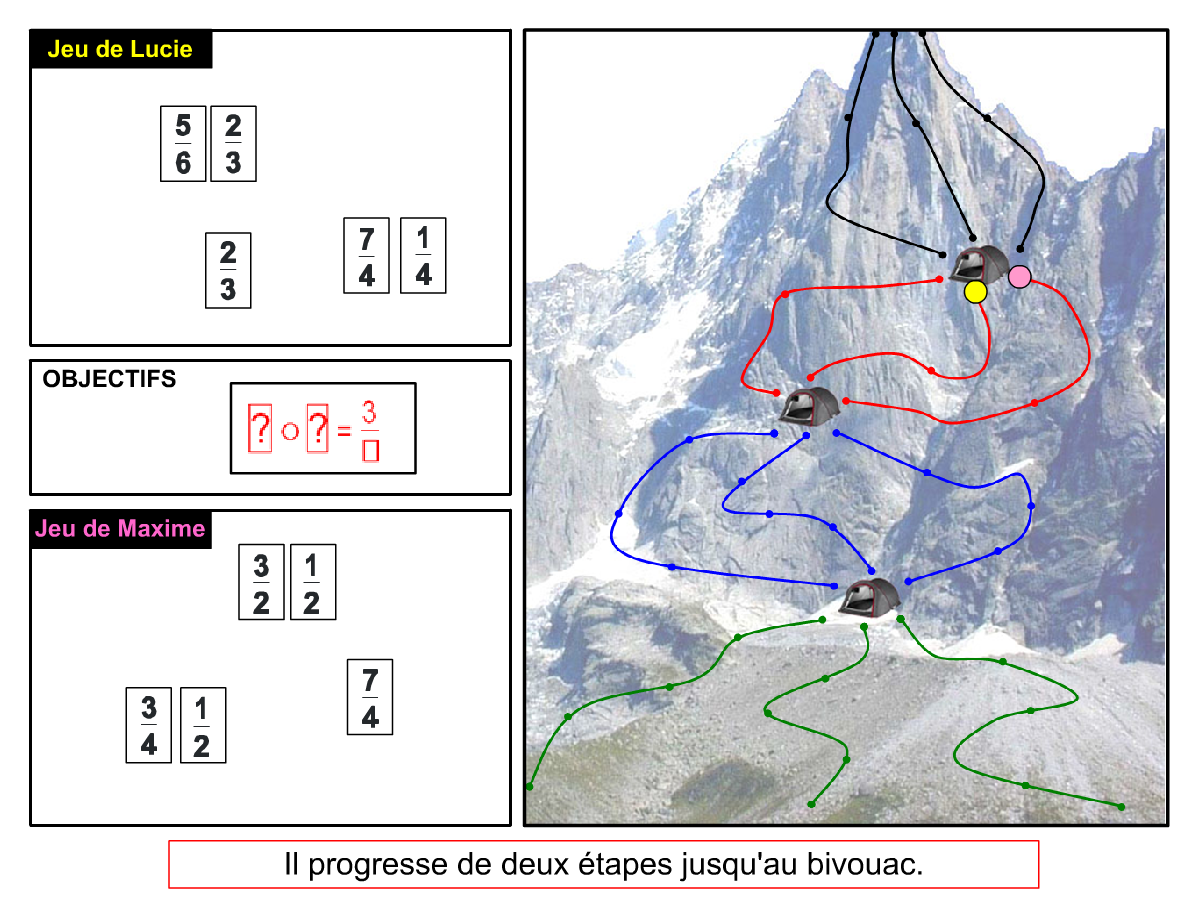
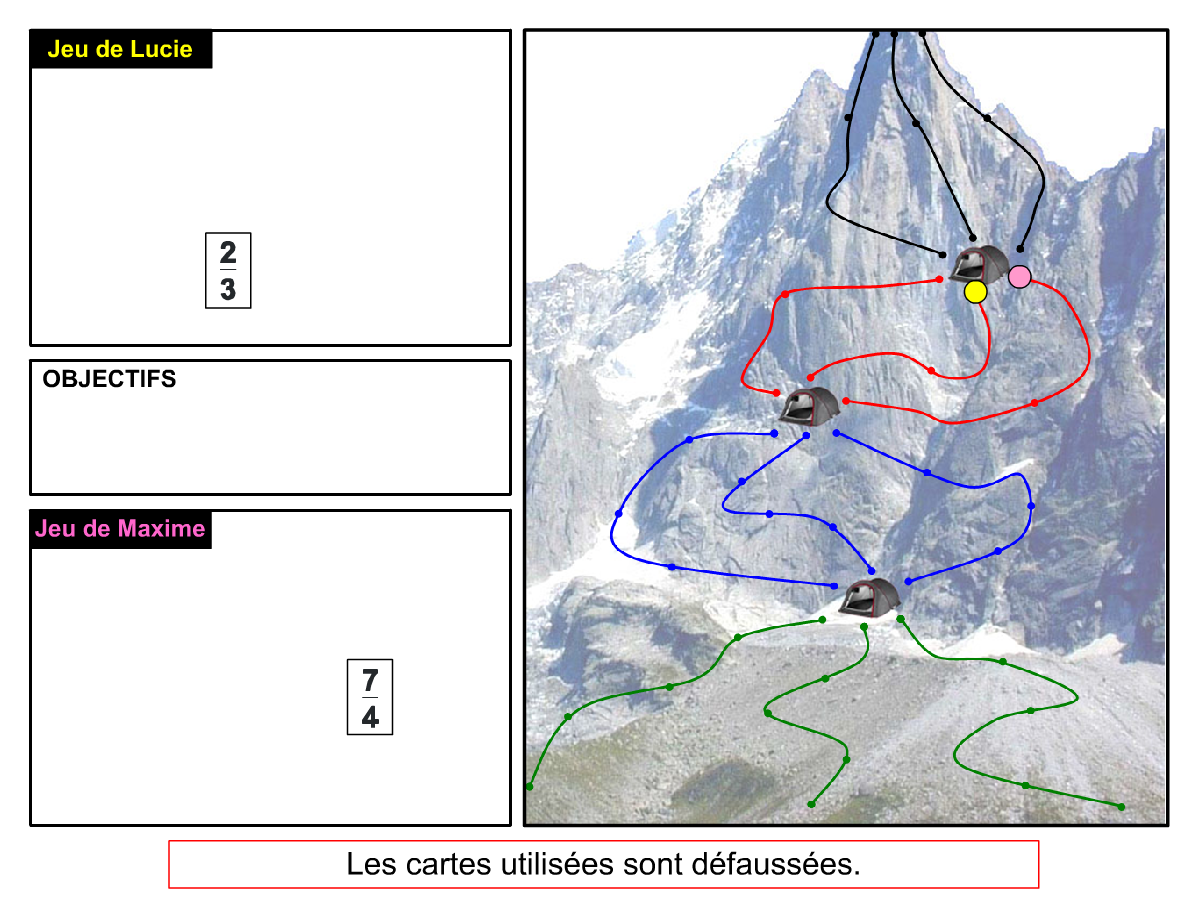
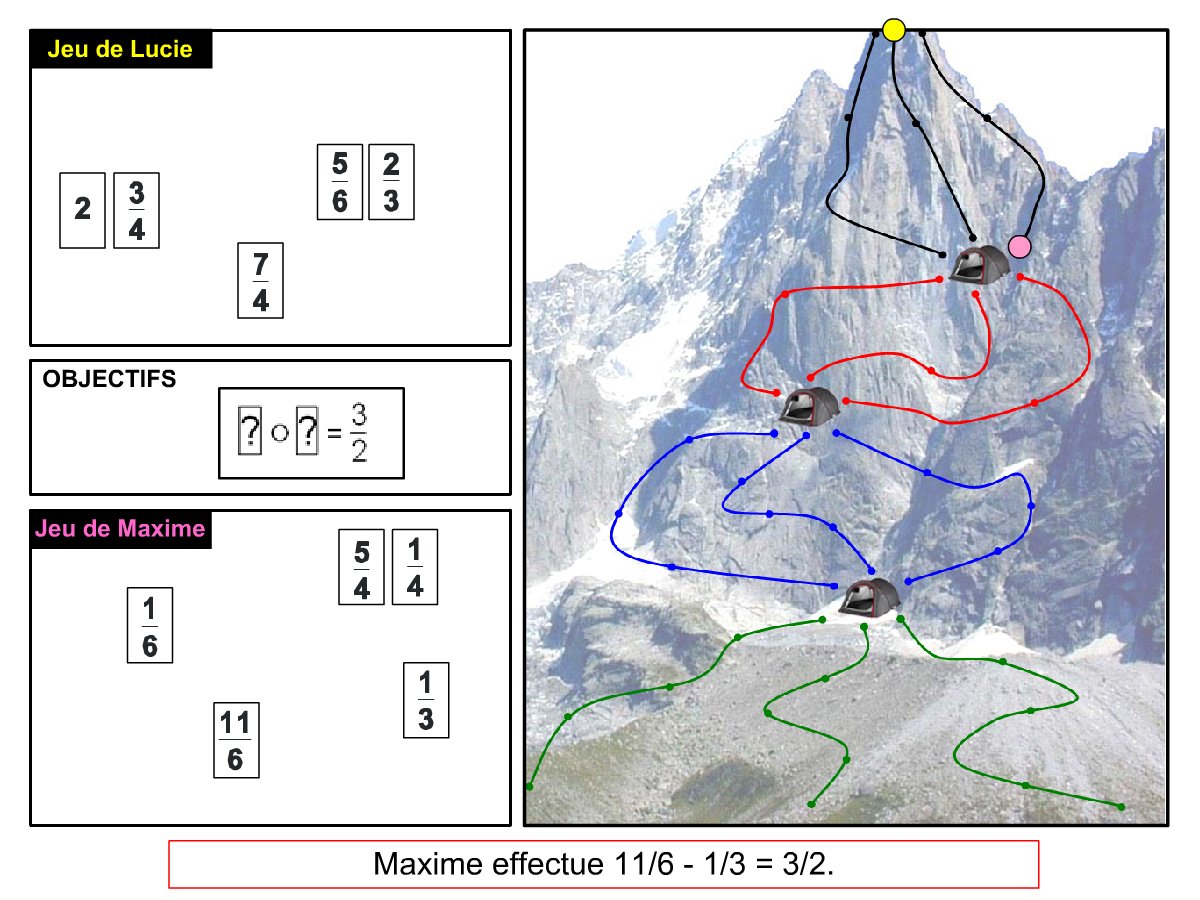
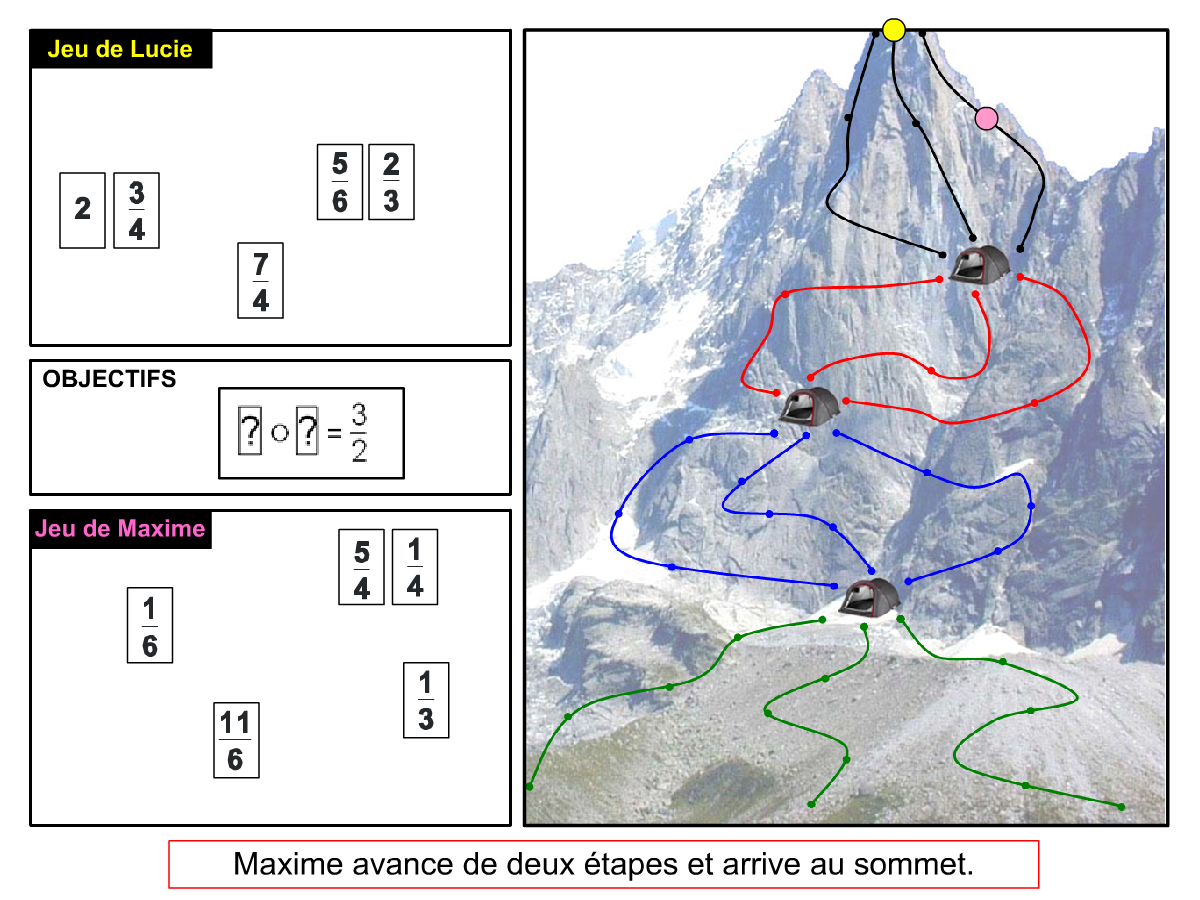
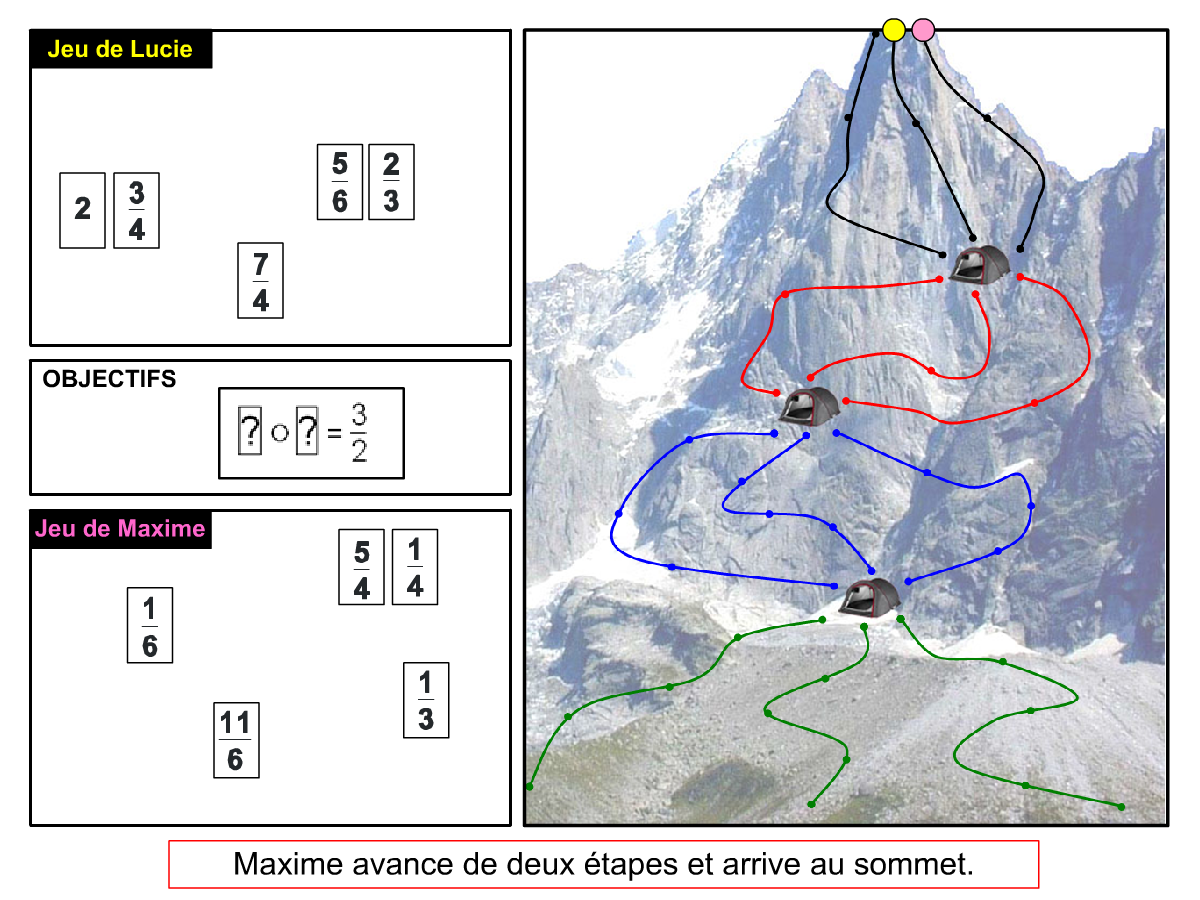
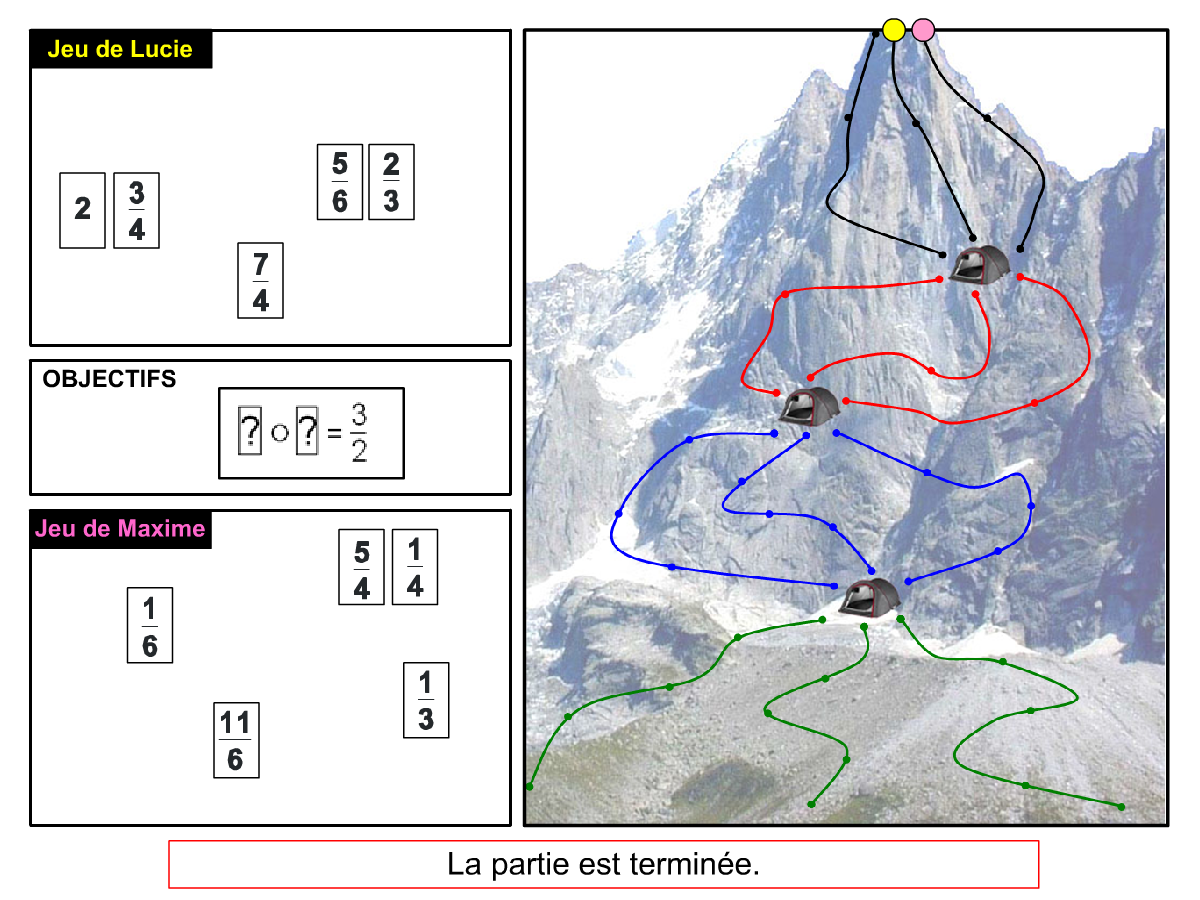
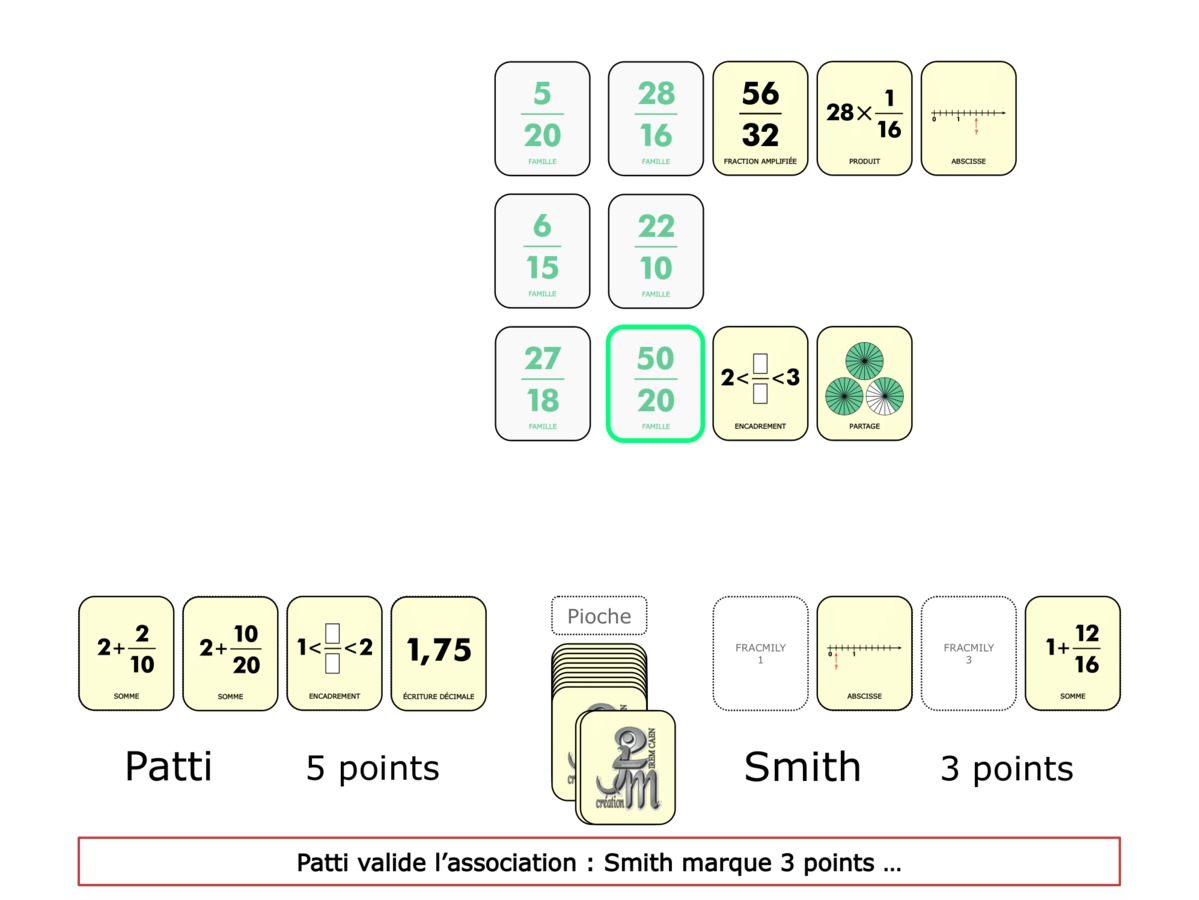
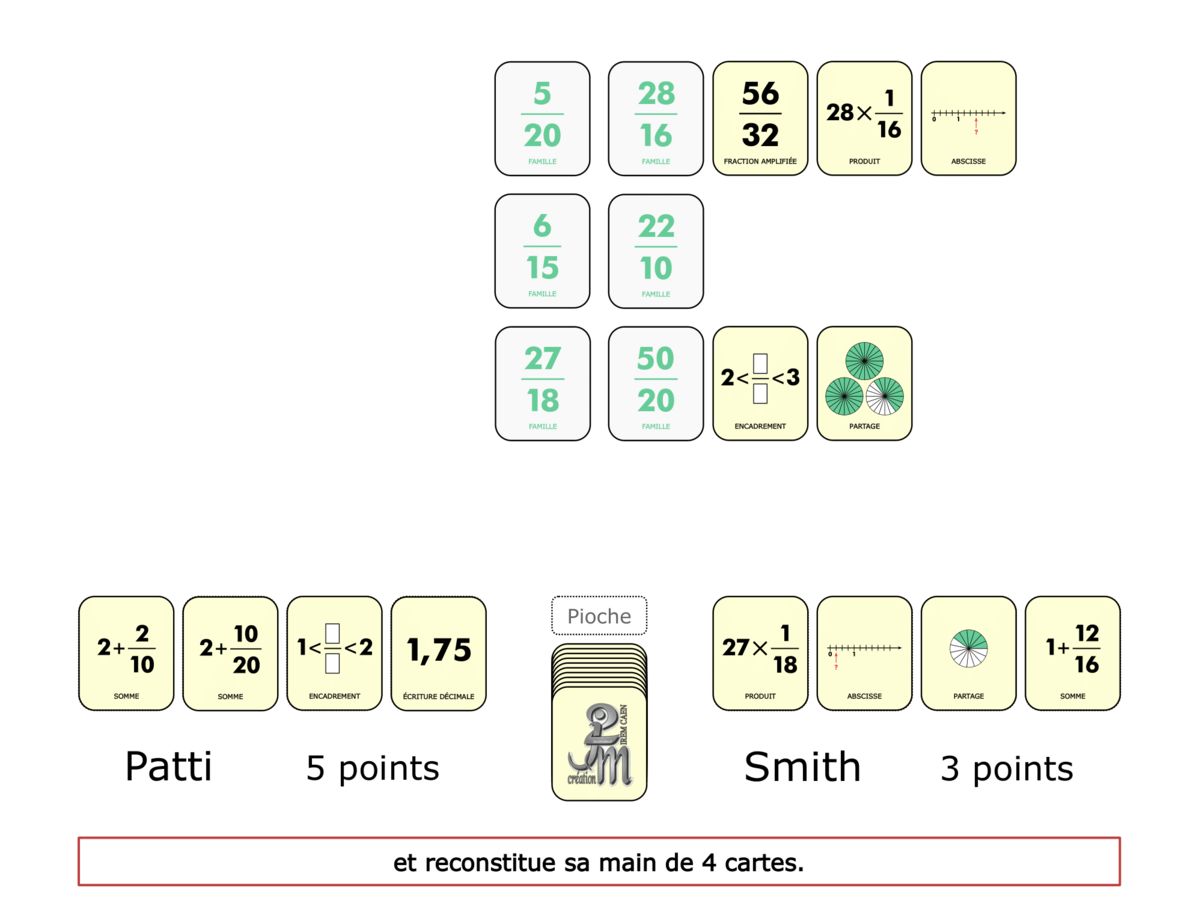
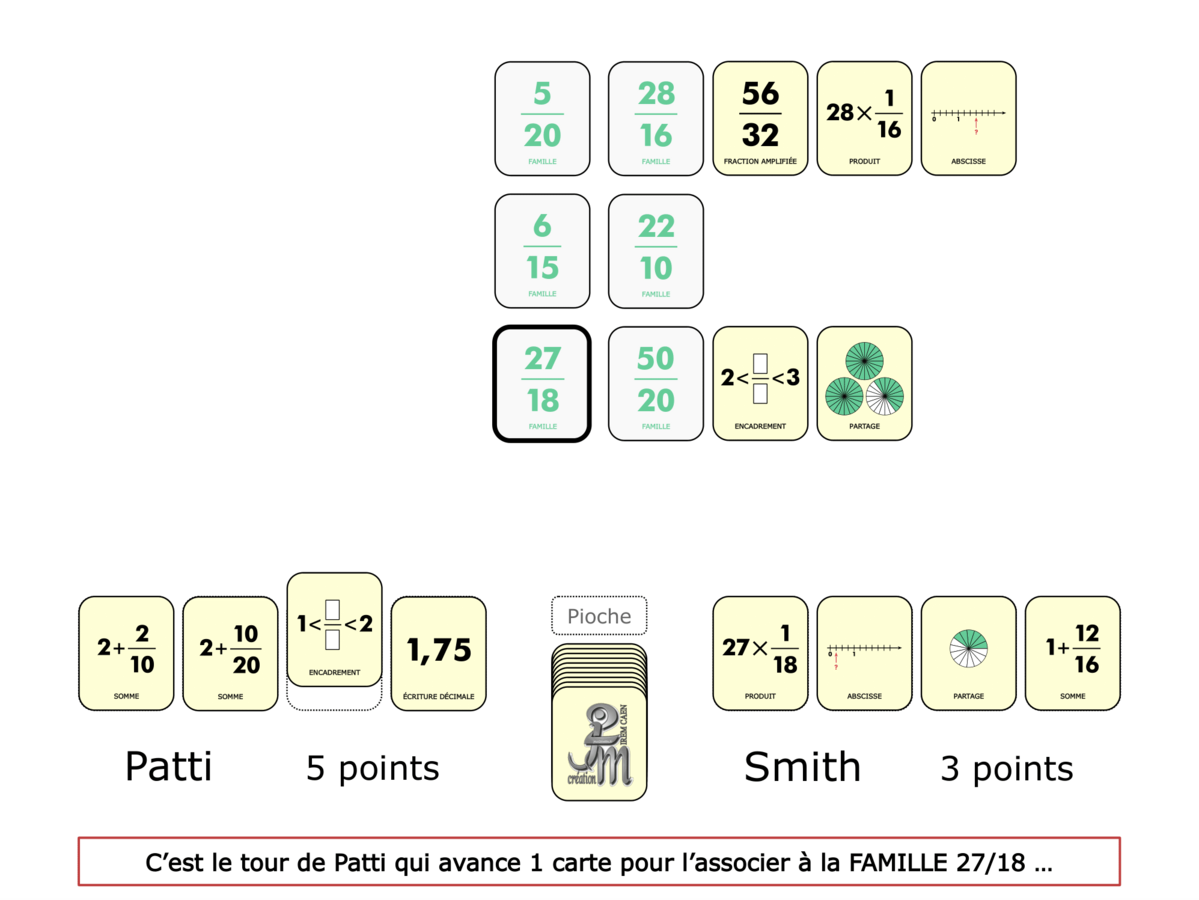
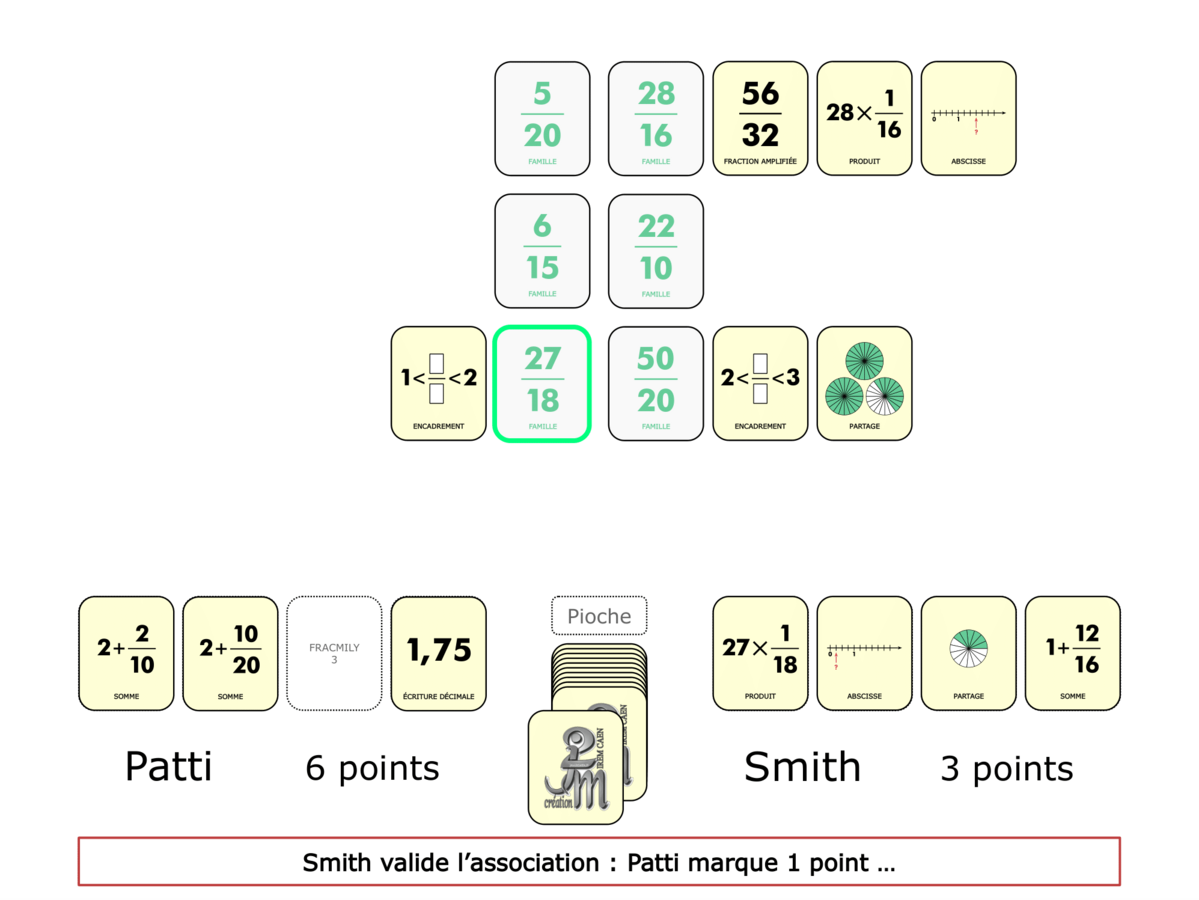
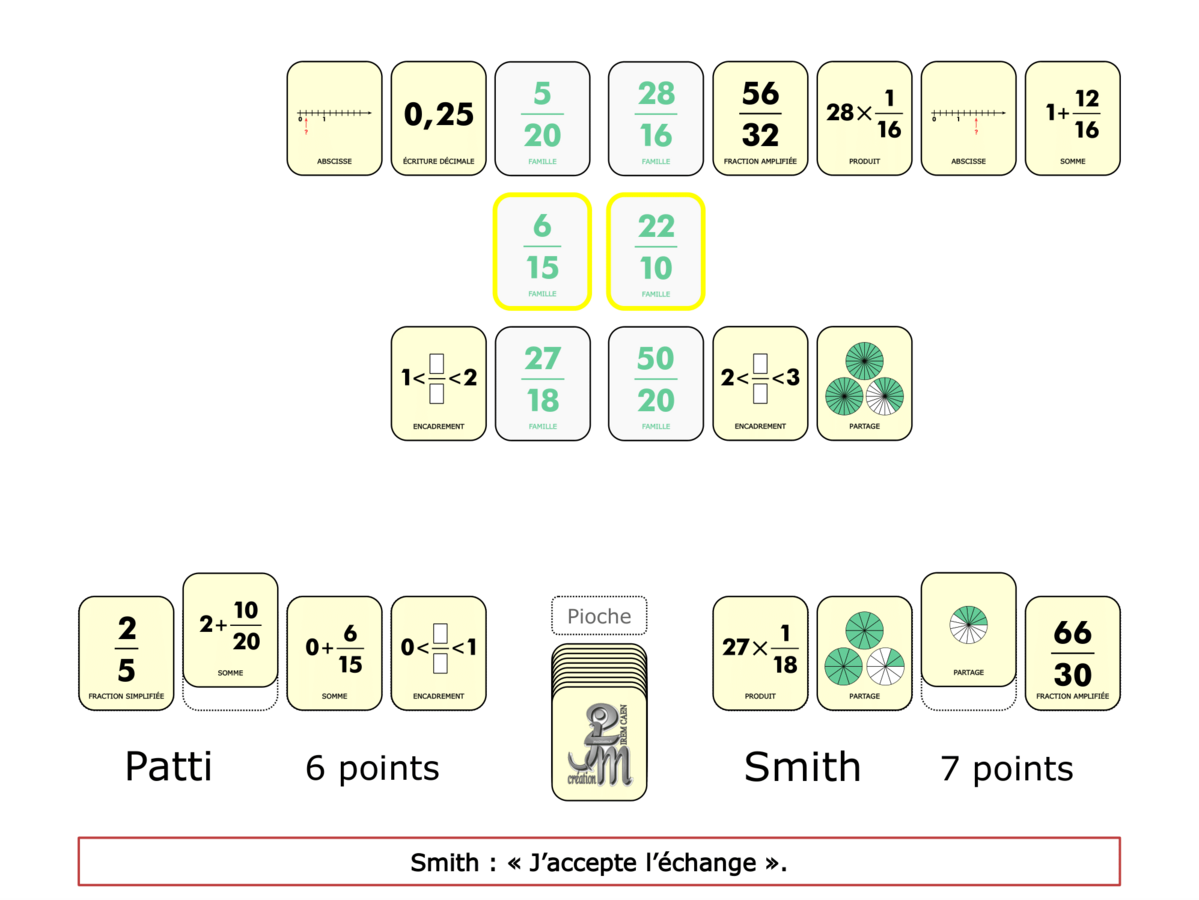
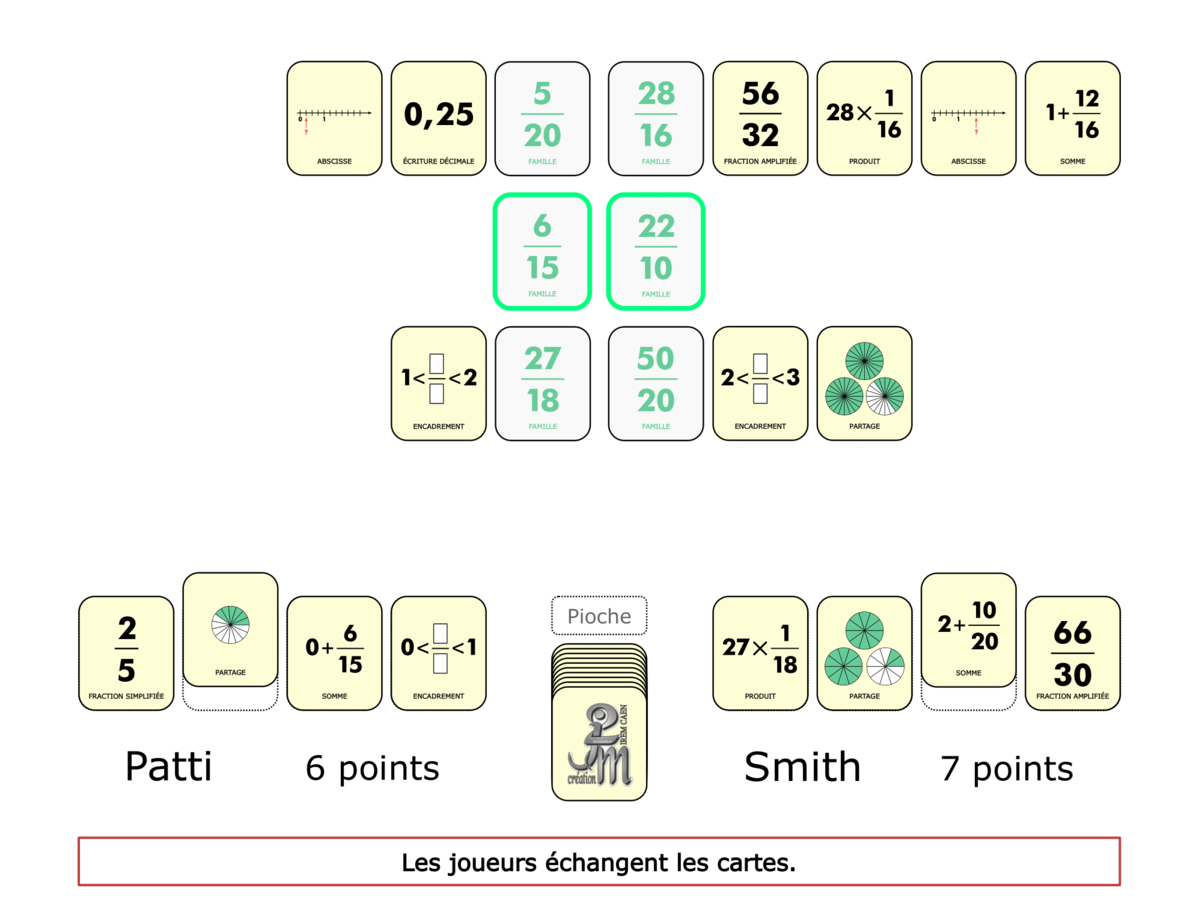
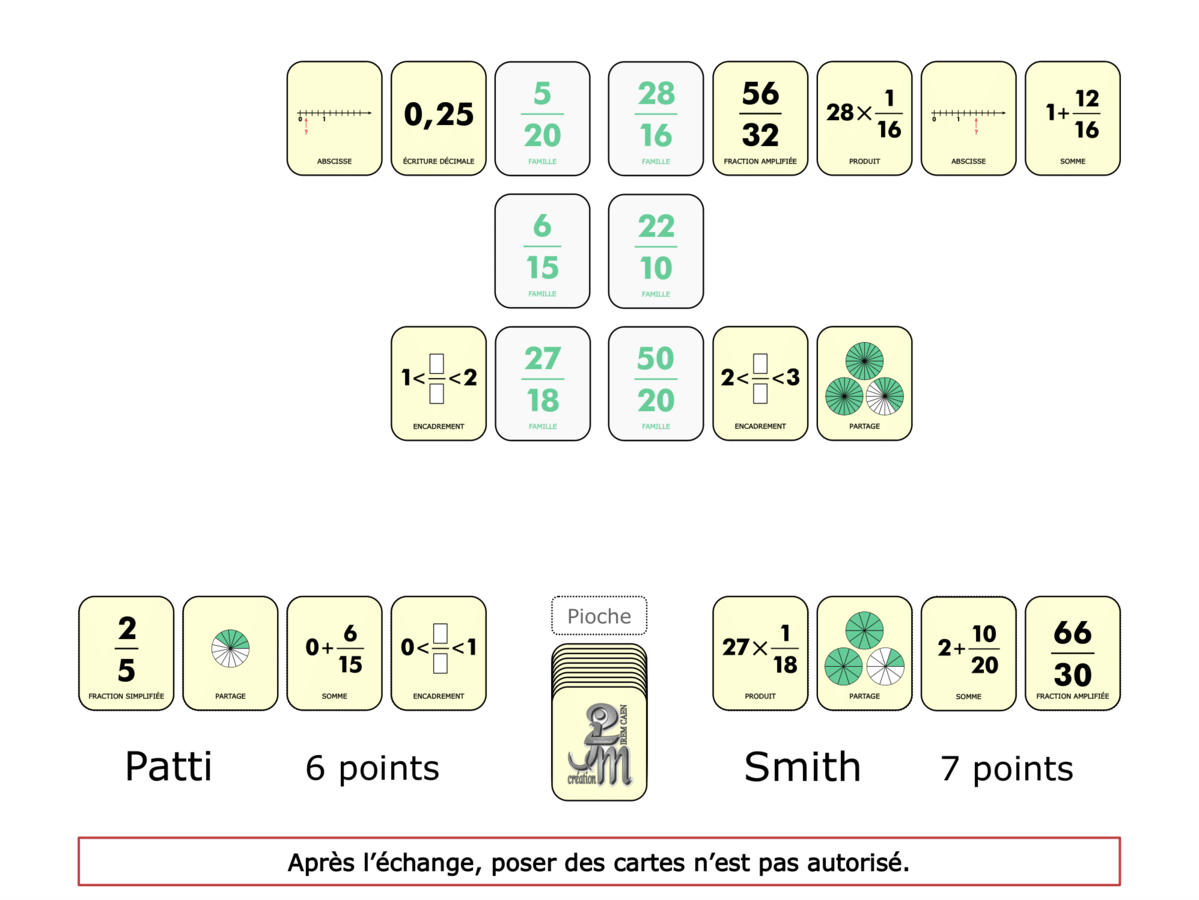
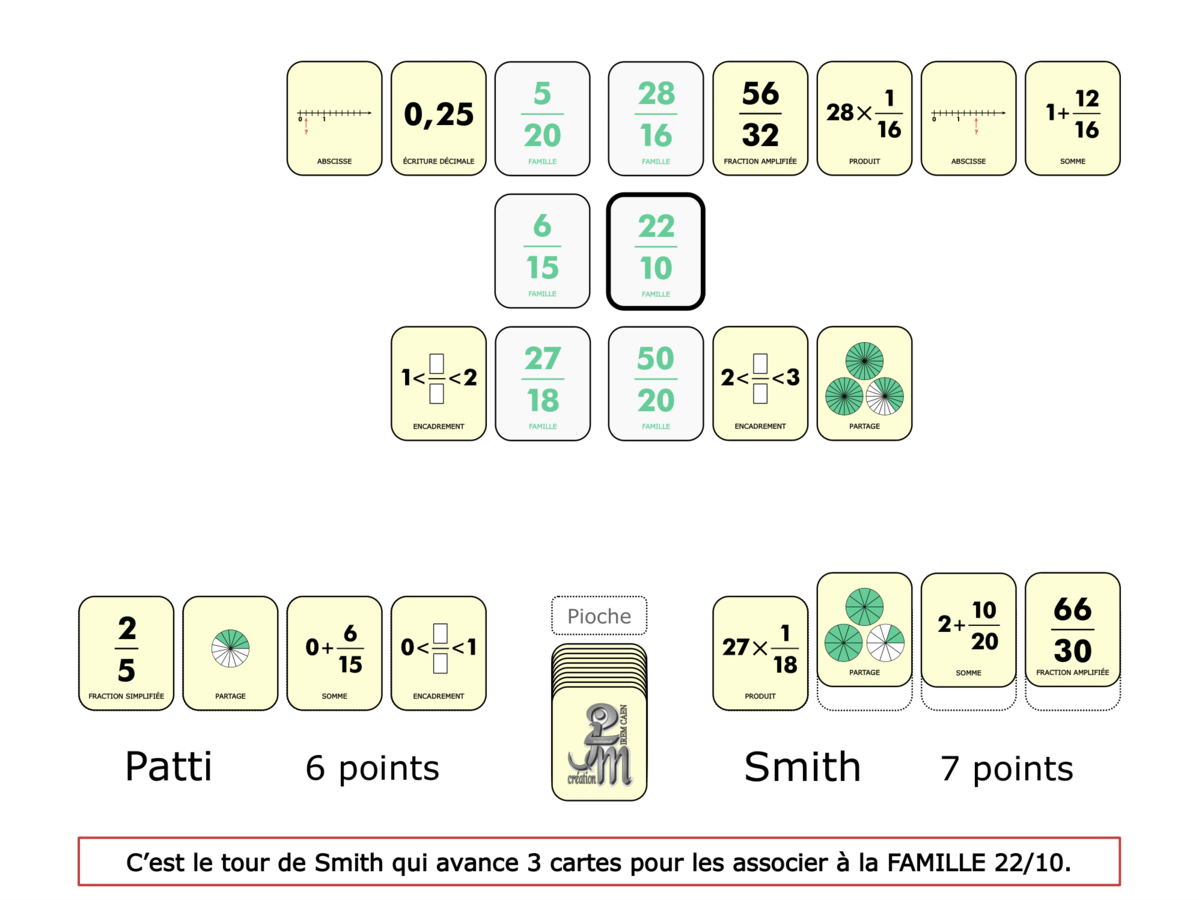
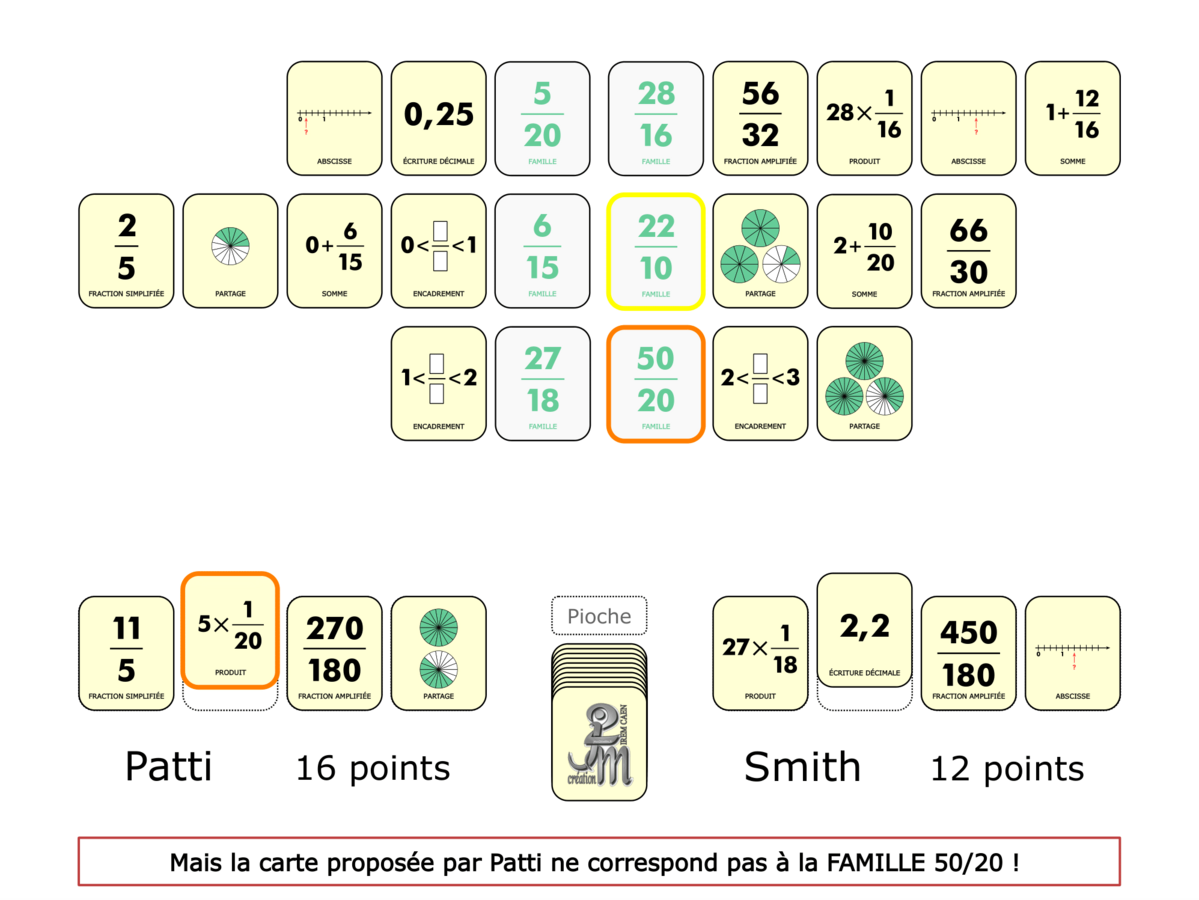
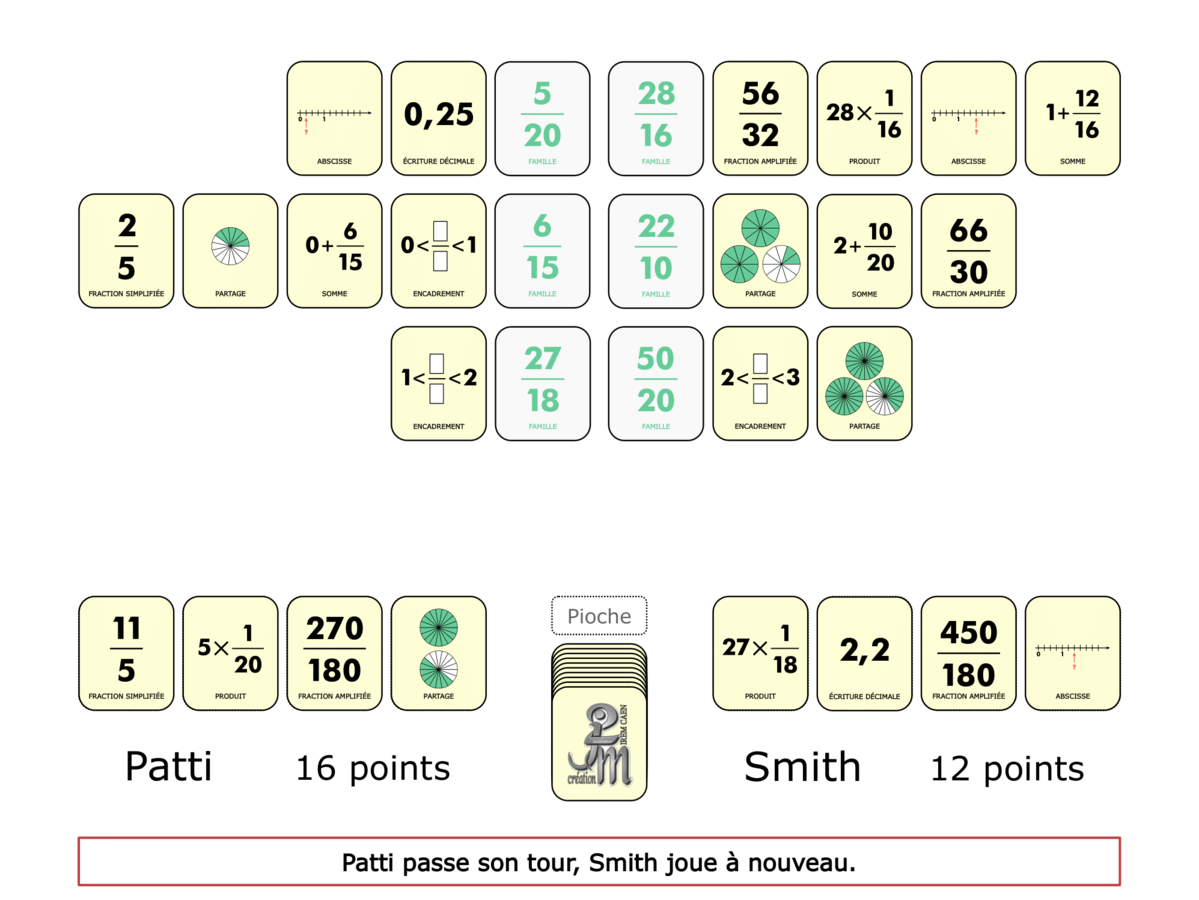
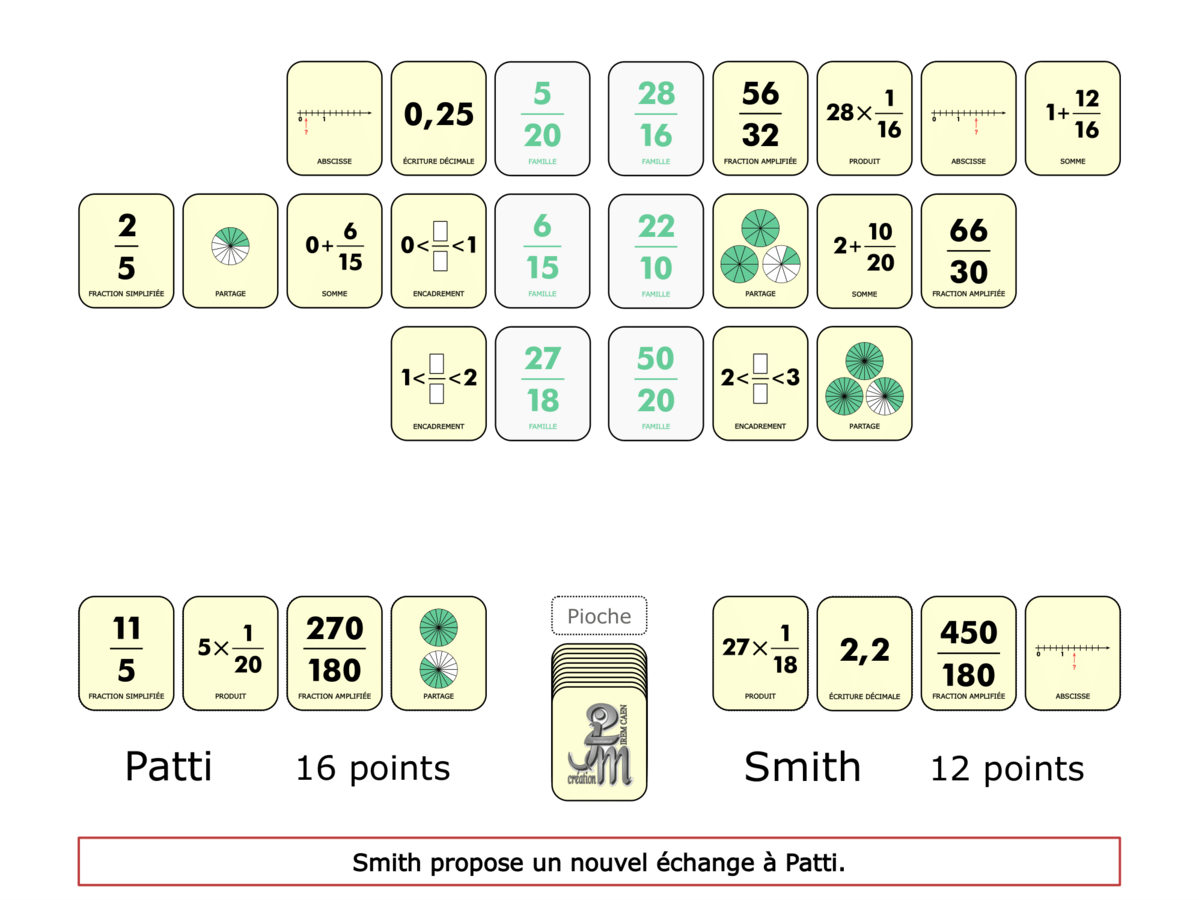
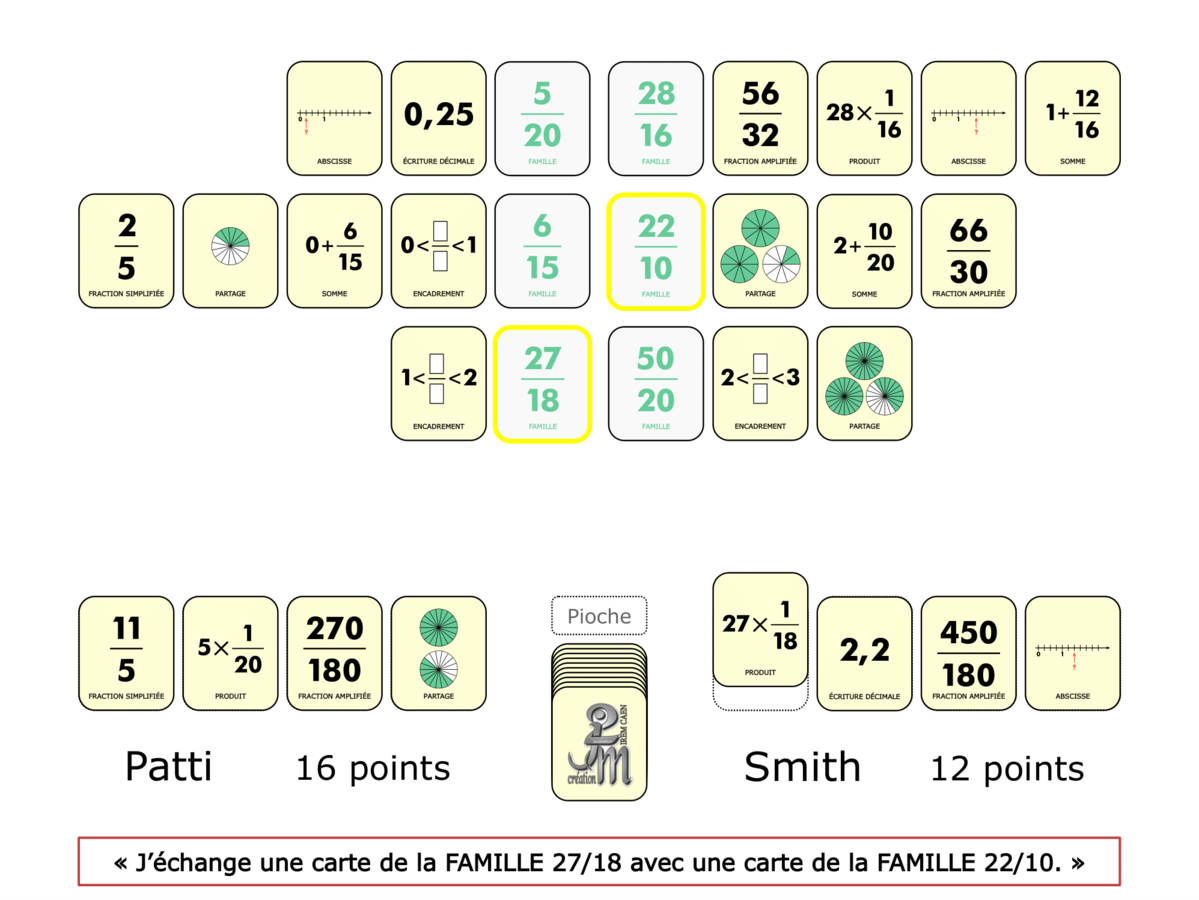
La Démo est un DIAPORAMA (ou une VIDEO) et contient le déroulement d’une partie (ou d’une séquence de partie) et peut être projetée aux élèves pour leur montrer le principe et le mécanisme de chaque jeu.
La règle du jeu
Dans un fichier PDF, elle vous donnera tous les détails concernant le fonctionnement du jeu. Cette règle est destinée aux enseignants, non aux élèves.
Les fichiers
Dans un fichier PDF, ils comportent tous les éléments indispensables à la fabrication et à l’utilisation du jeu tels que les cartes, pions, plateaux, feuilles de marque…
Nous espérons que tous ces documents vous permettront de tirer pleinement parti des jeux que nous proposons sur ce site. Si d’aventure vous aviez des questions, remarques ou suggestions, n’hésitez pas à nous écrire (merci d’utiliser la page CONTACT), la critique constructive ne pourra que nous aider à progresser.
CONCEPTION DE NOS JEUX
Il ne s’agit pas, dans notre conception du jeu, de seulement donner un aspect ludique à une activité mathématique ; beaucoup de travaux de ce type ont été développés depuis de nombreuses années par les enseignants (par exemple le groupe «Jeux» de l’APMEP), avec succès, et ont rendu la pratique des mathématiques plus attractive pour les élèves.
Notre objectif se veut plus restrictif et pour qu’une activité puisse bénéficier d’une appellation «jeu», elle doit avoir un aspect jeu de société et répondre à certains critères.
Notre volonté est avant tout de donner à ce que nous appelons «jeu» un caractère de challenge, que ce soit avec d’autres (envie de gagner la partie) ou avec soi-même (envie de se dépasser, de faire mieux).
Le jeu doit proposer à l’élève un but différent de ceux auxquels il est habitué tels que répondre à une question ou résoudre un problème. Ici, il s’agit plutôt d’utiliser des outils mathématiques à des fins qui ne le sont pas, la motivation sera alors plus sociale que scolaire.
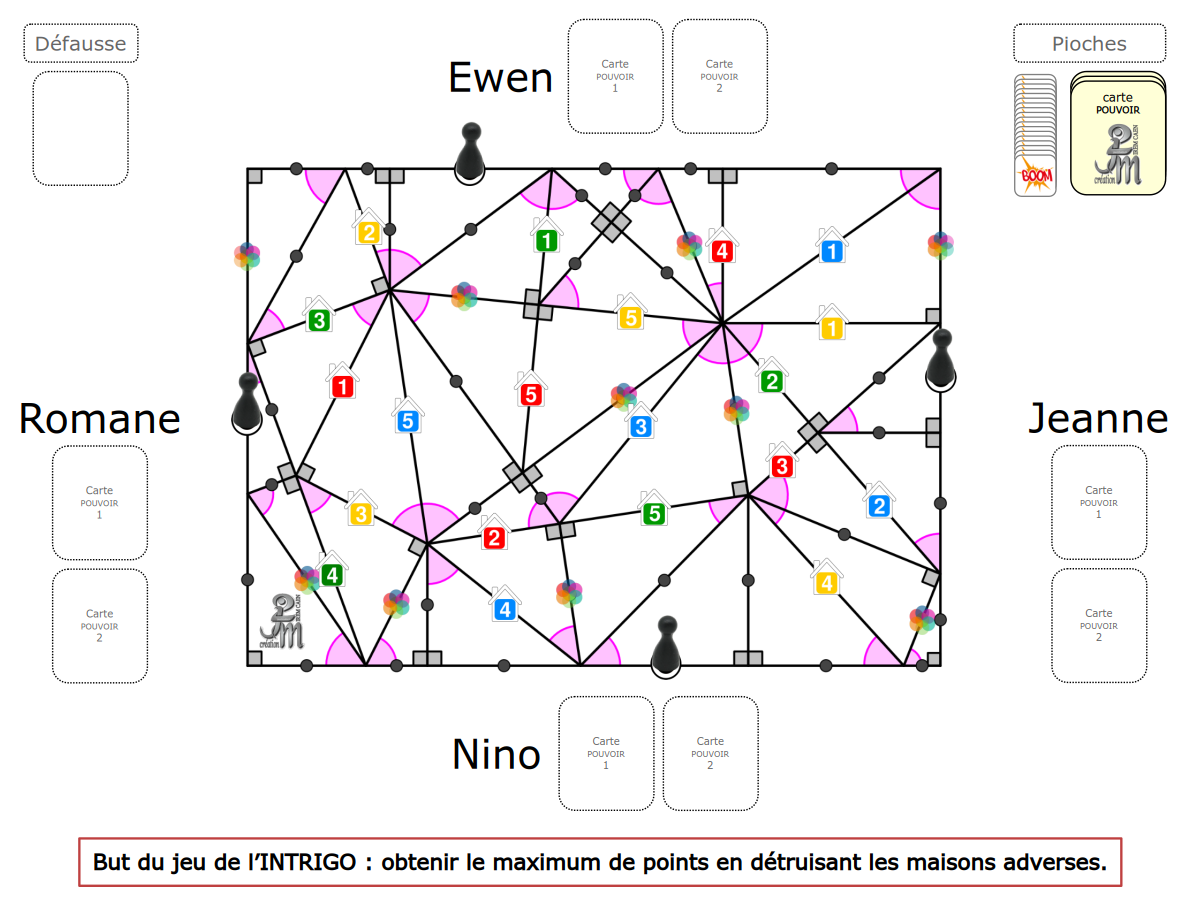
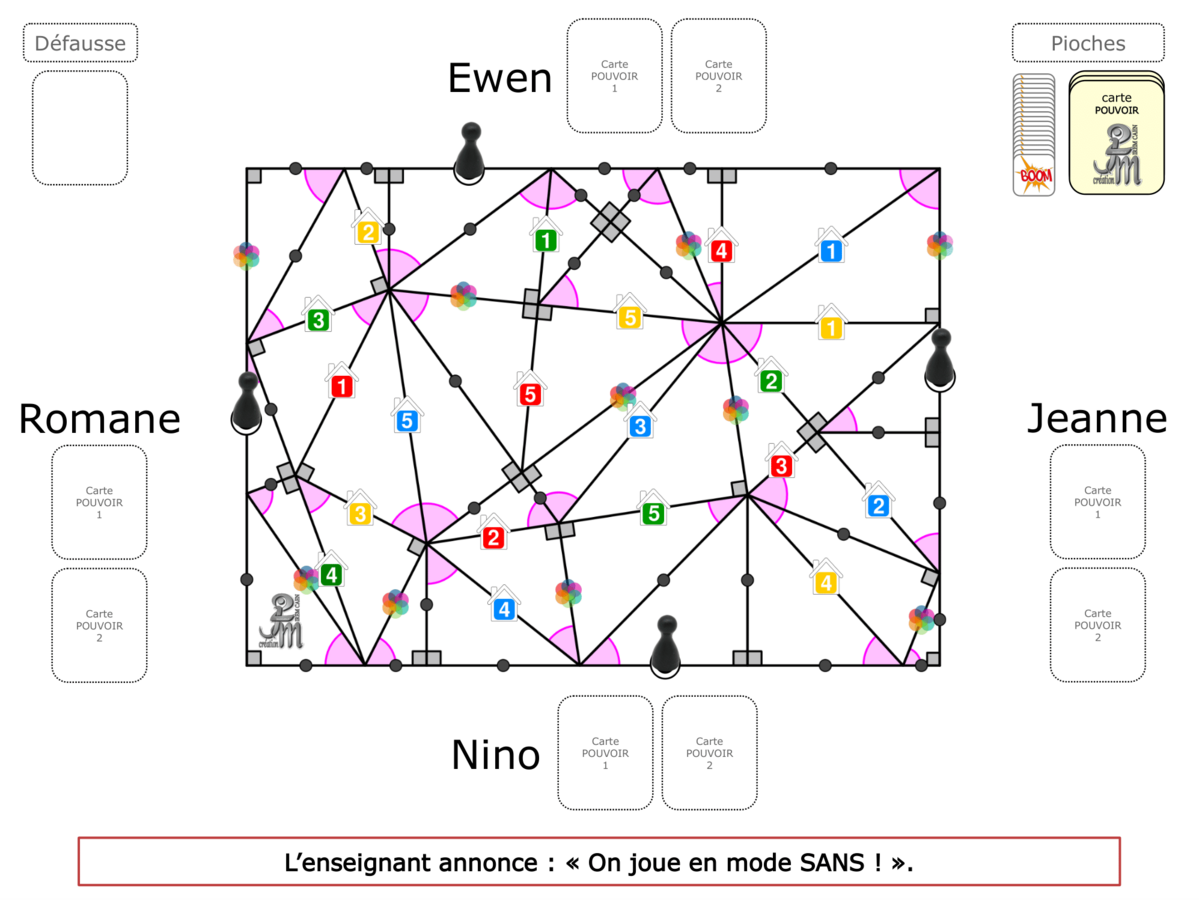
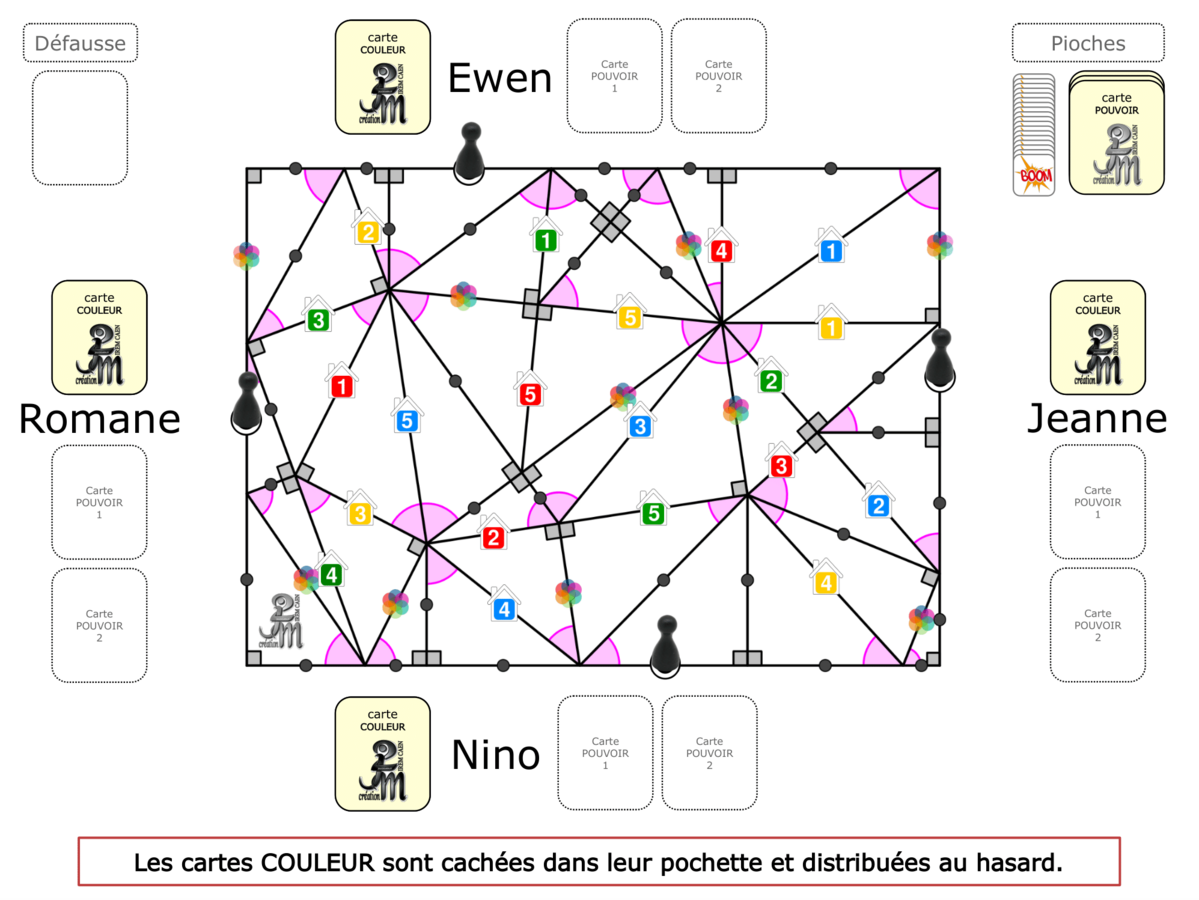
L’utilisation d’un matériel spécifique tel que pions, dés, plateaux ou cartes nous semble essentielle pour que l’élève se sente en situation de jouer. Lorsque le matériel leur est distribué, il est clairement identifié comme matériel de jeu ; l’activité paraît alors moins scolaire, et de ce fait devient plus séduisante, voire intrigante.
La progression des parties s’effectue par étapes, et chaque «coup» joué fait fonctionner la notion mathématique utilisée.
La règle du jeu, outre des principes mathématiques, comporte des aspects d’ordre technique qui doivent rester abordables par tous. Une trop grande complexité du fonctionnement du jeu risquerait d’être un élément perturbateur dans l’utilisation des règles mathématiques et nuirait aux objectifs pédagogiques visés.
Les erreurs doivent être sanctionnées par des «malus» (passer son tour, reculer sur un parcours), dans le but d’obliger chaque élève à avoir un regard critique sur ce qu’il fait ou ce que fait l’autre.
Notre préoccupation est axée sur la manipulation de notions qui posent problème sans forcément recourir à un cadre qui puisse faire croire à un aspect non mathématique du jeu ; il n’est pas nécessaire de donner un décor artificiel à un jeu pour le rendre attractif, il est certainement plus important de soigner le fond que la forme.
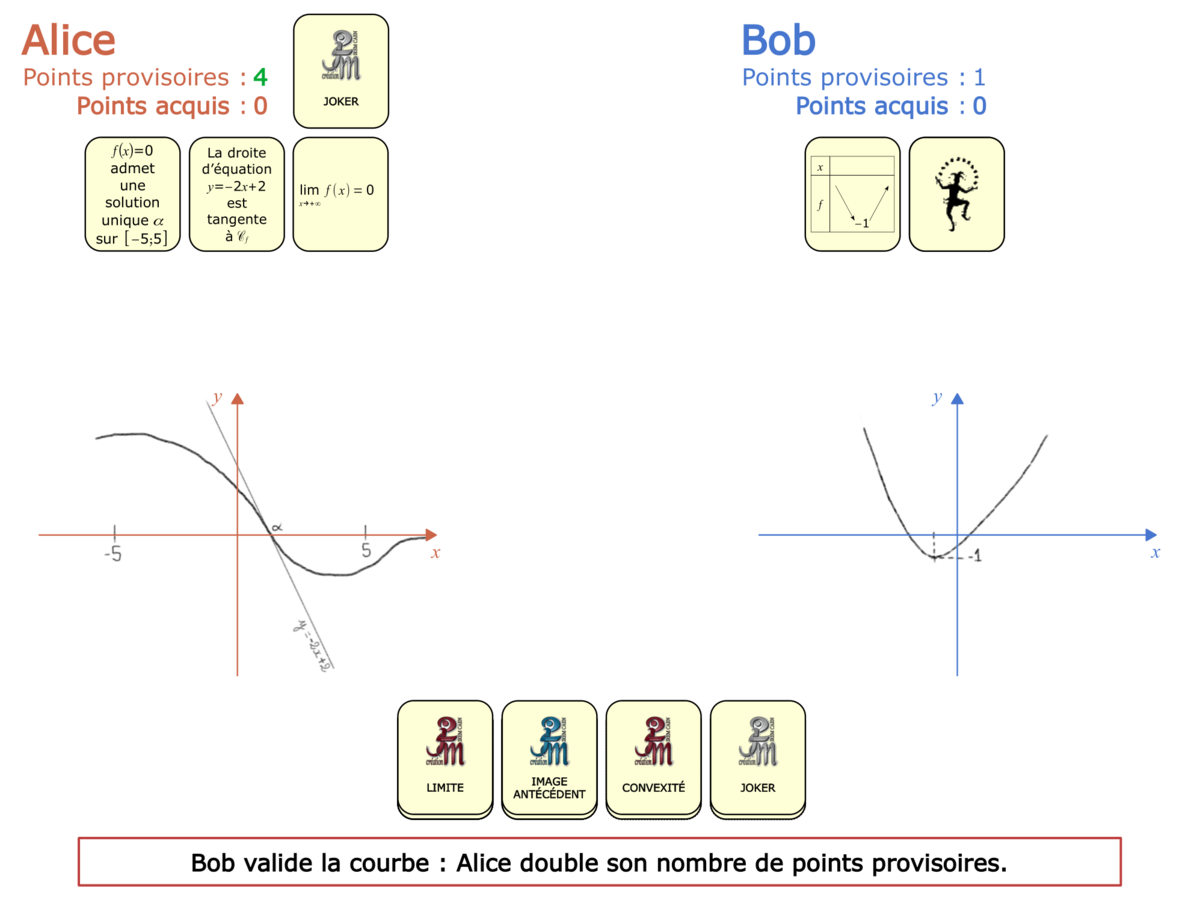
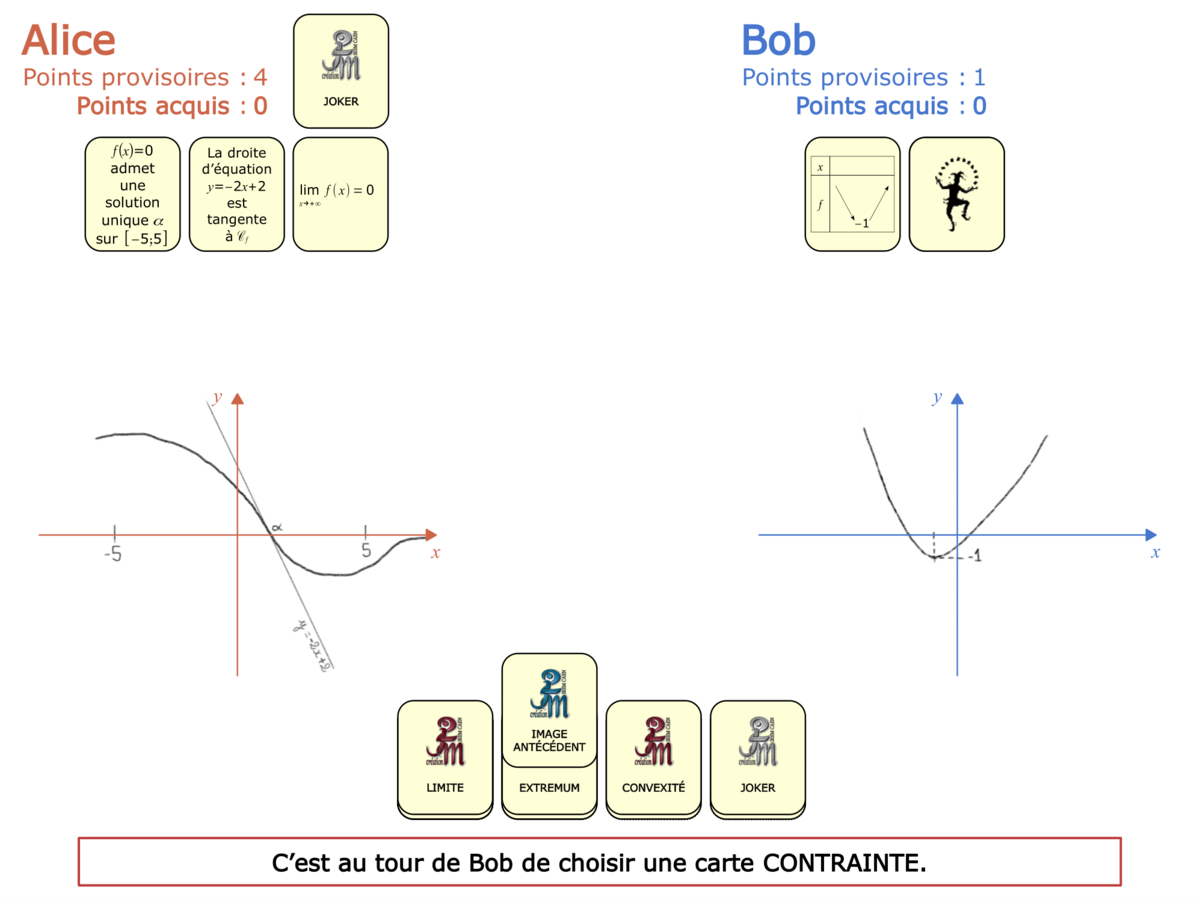
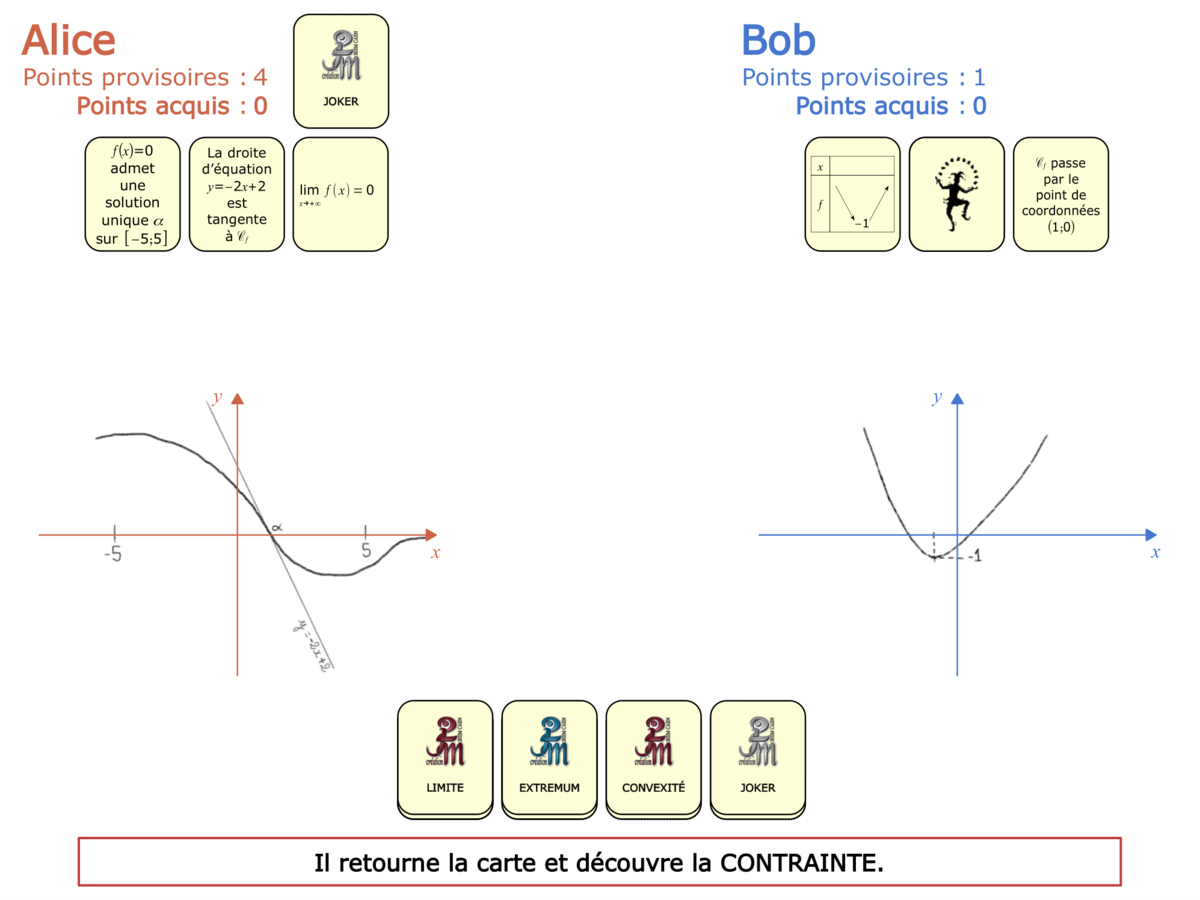
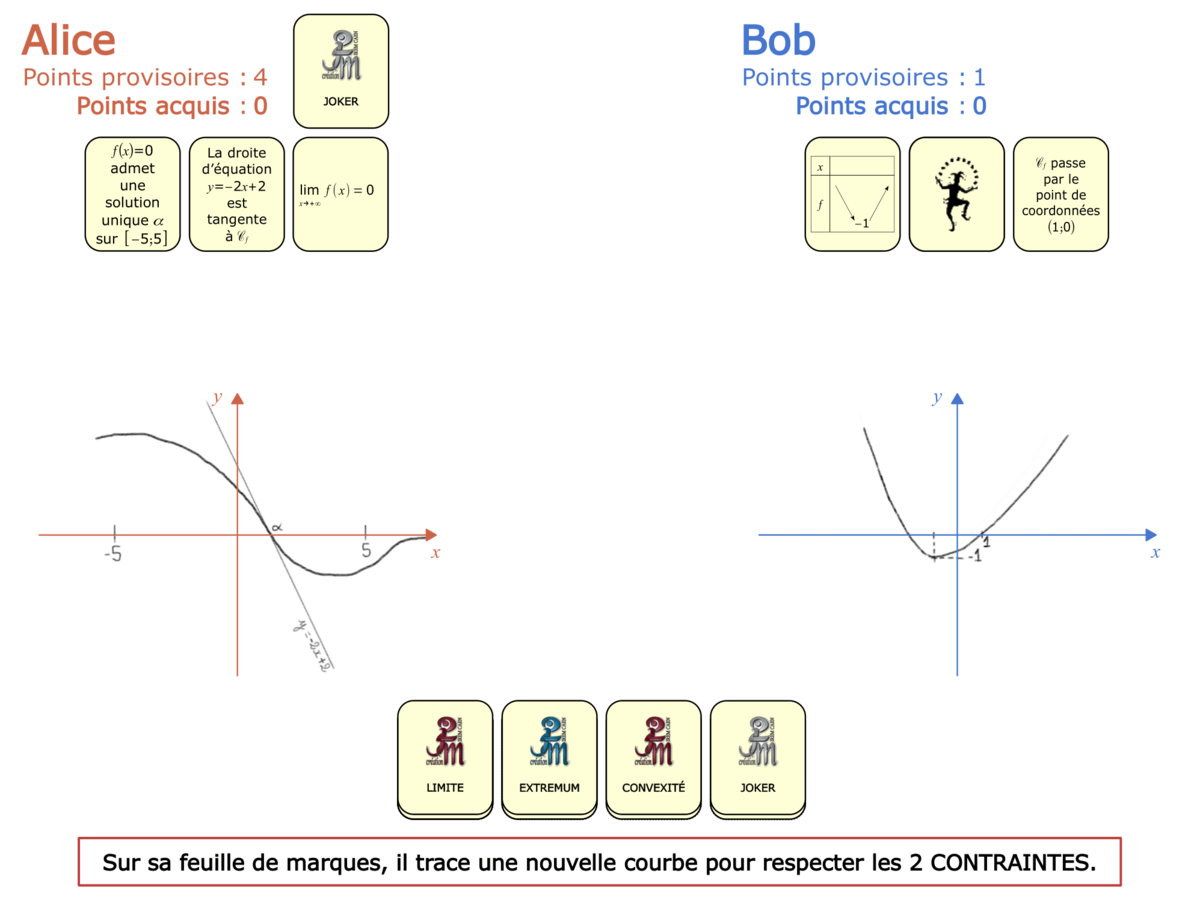
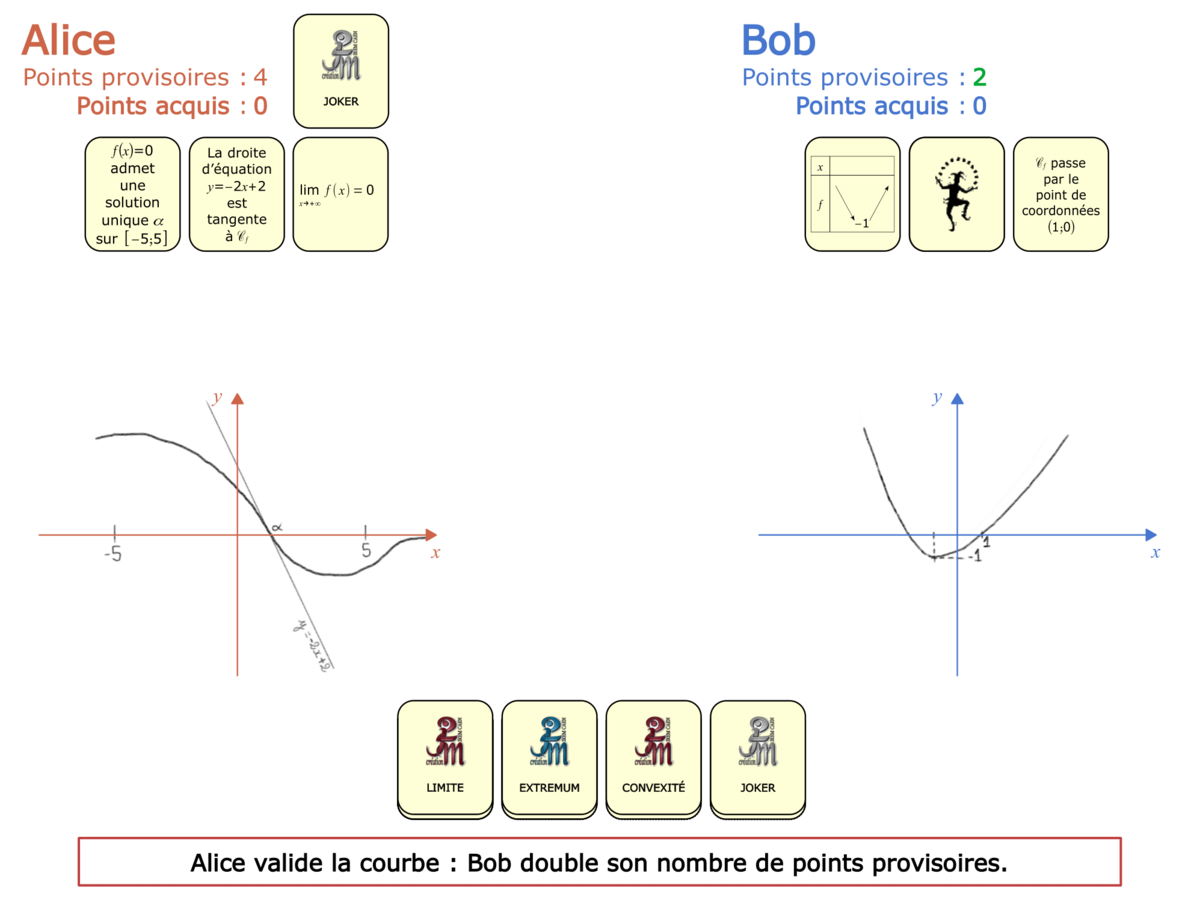
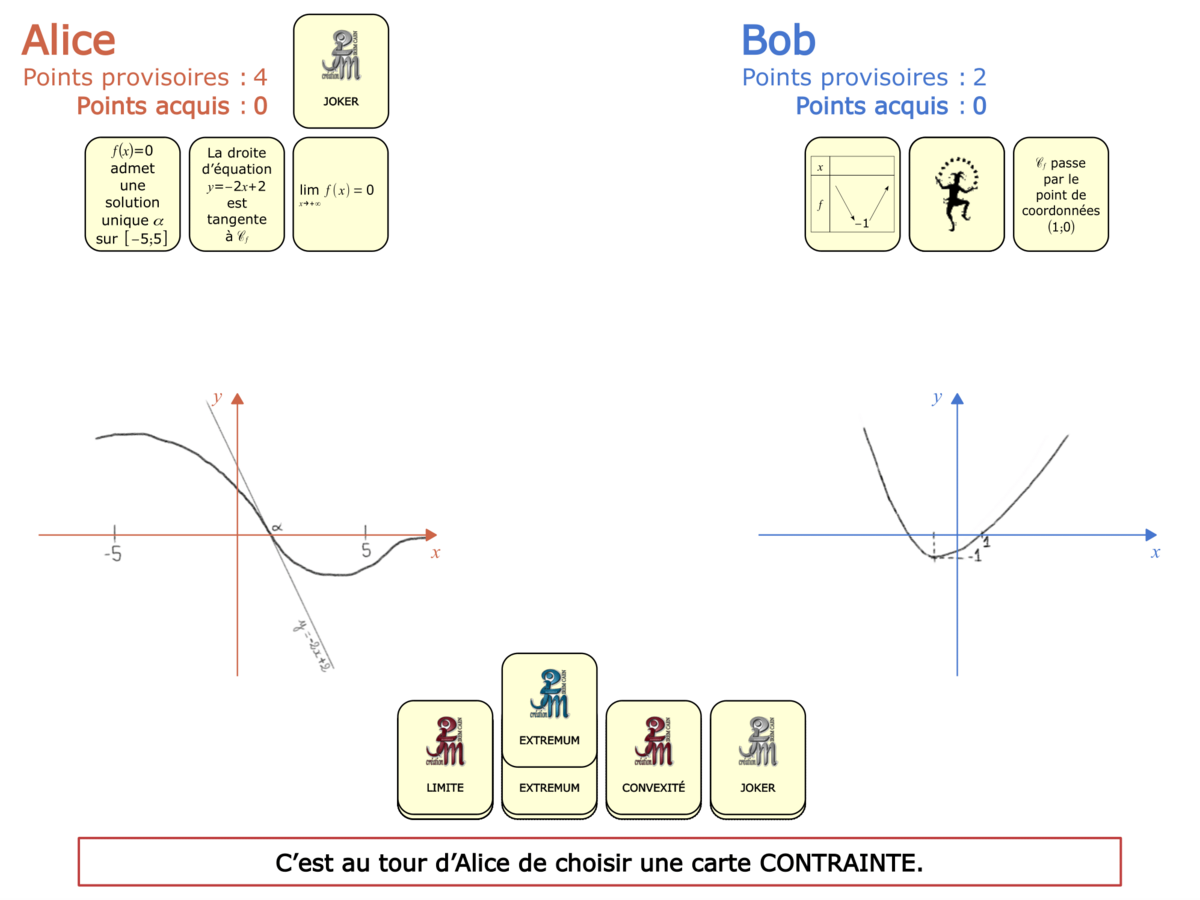
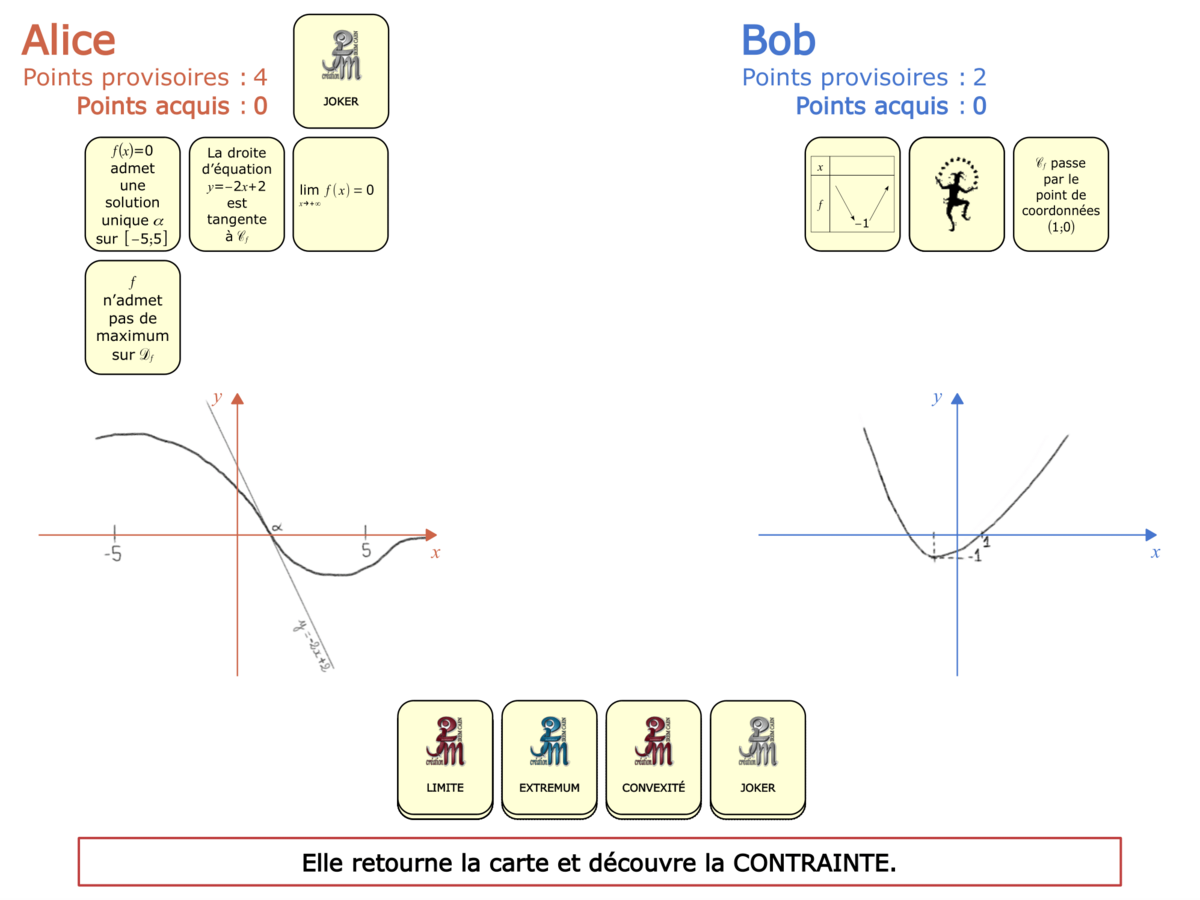
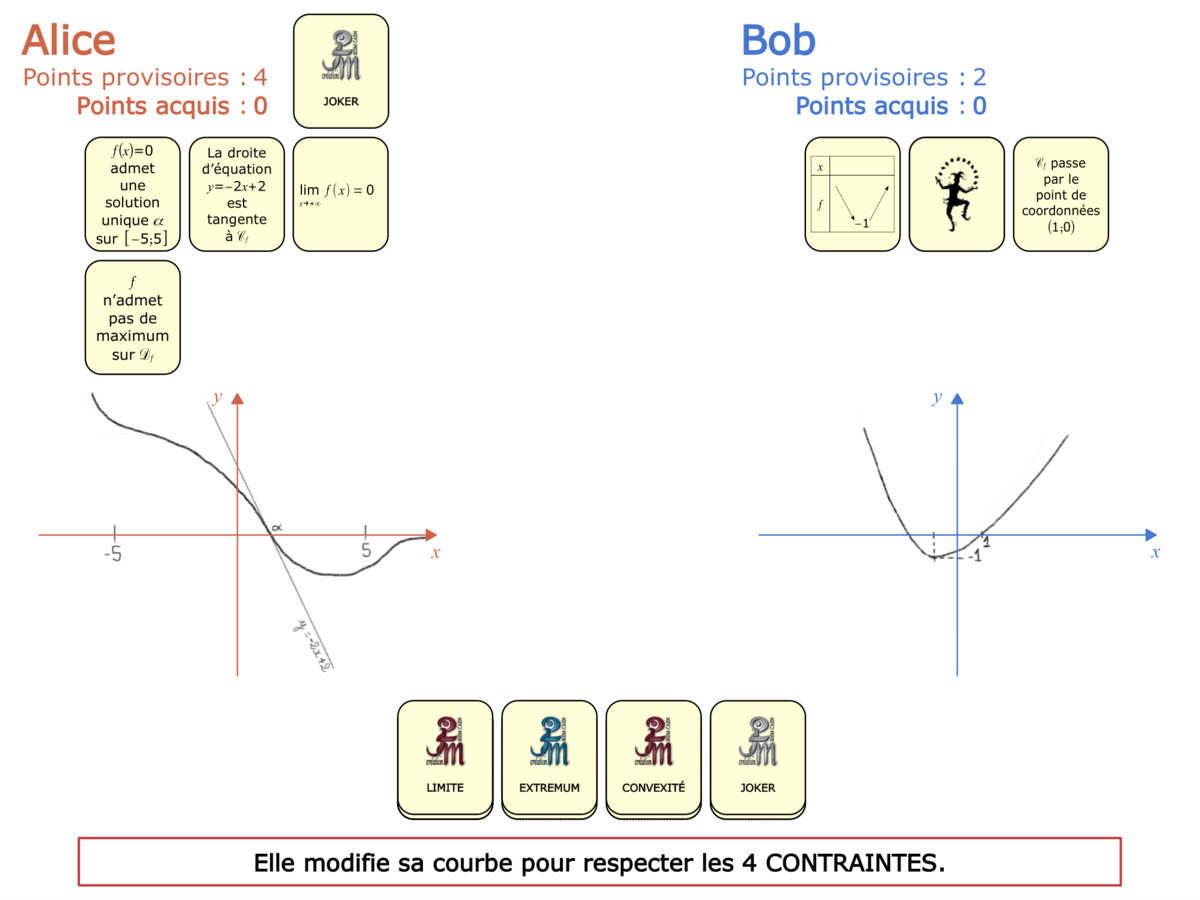
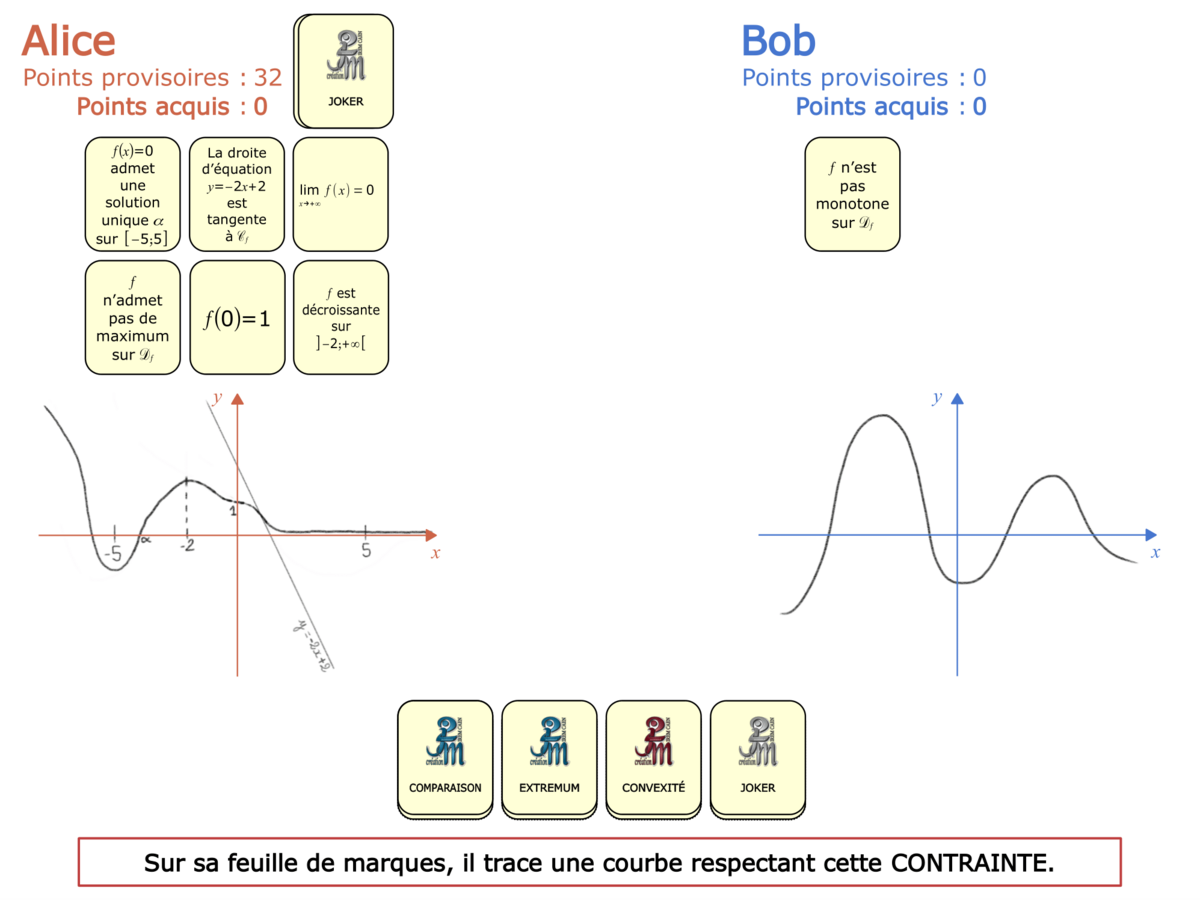
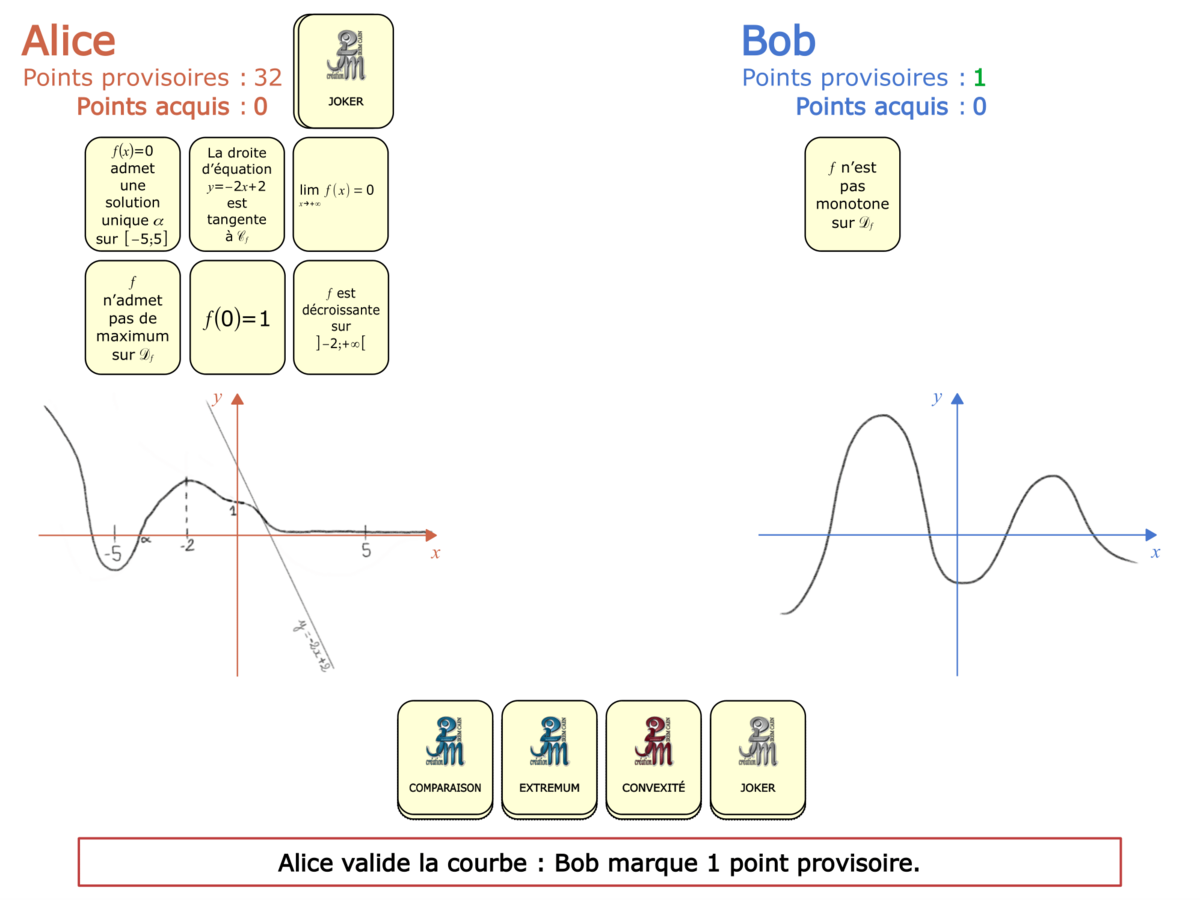
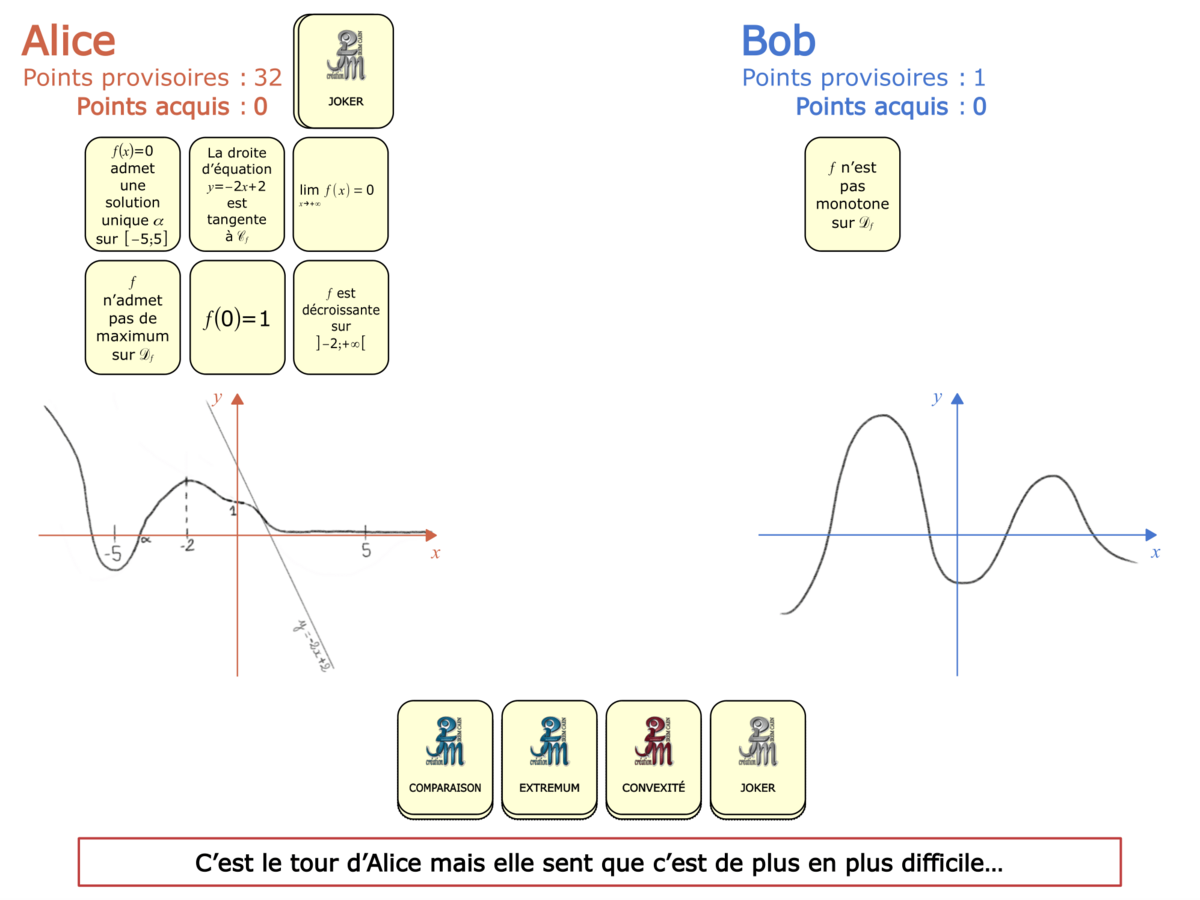
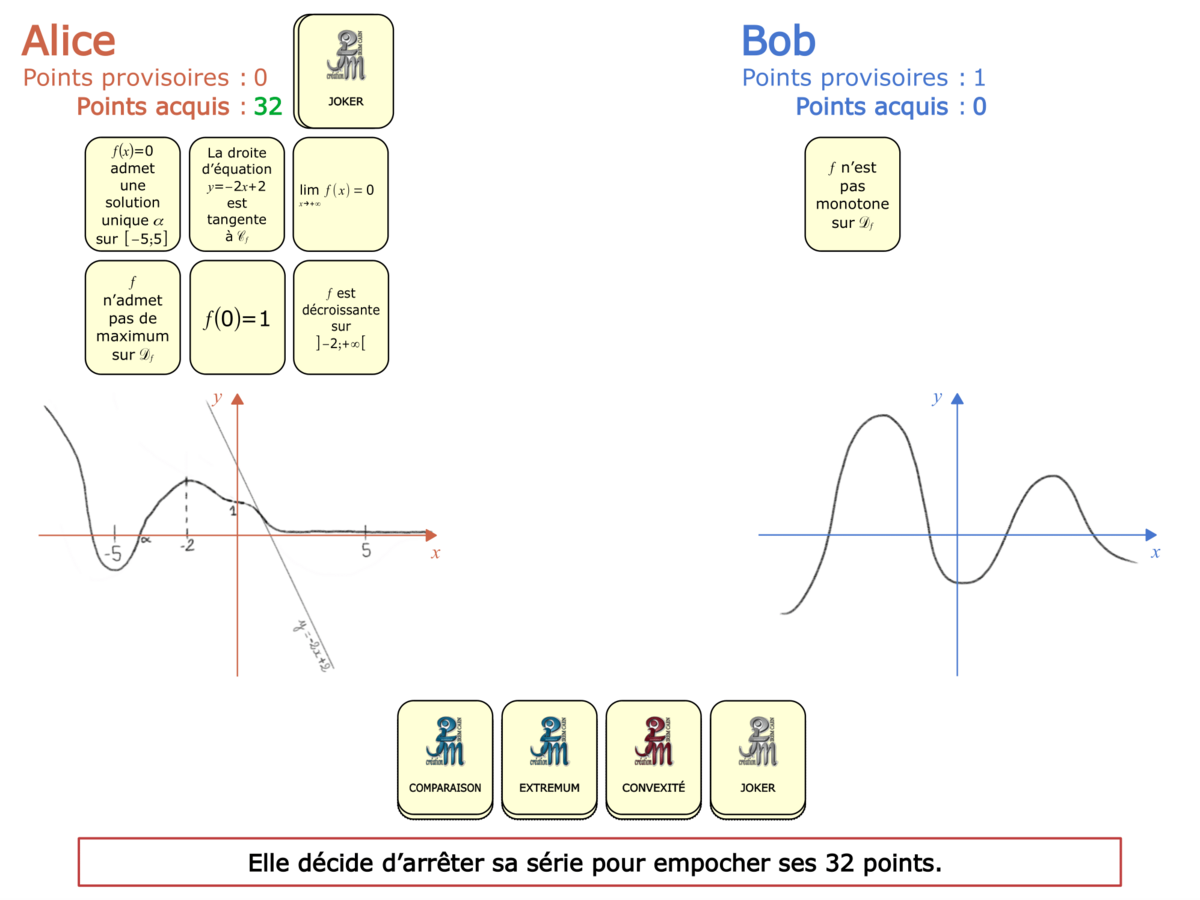
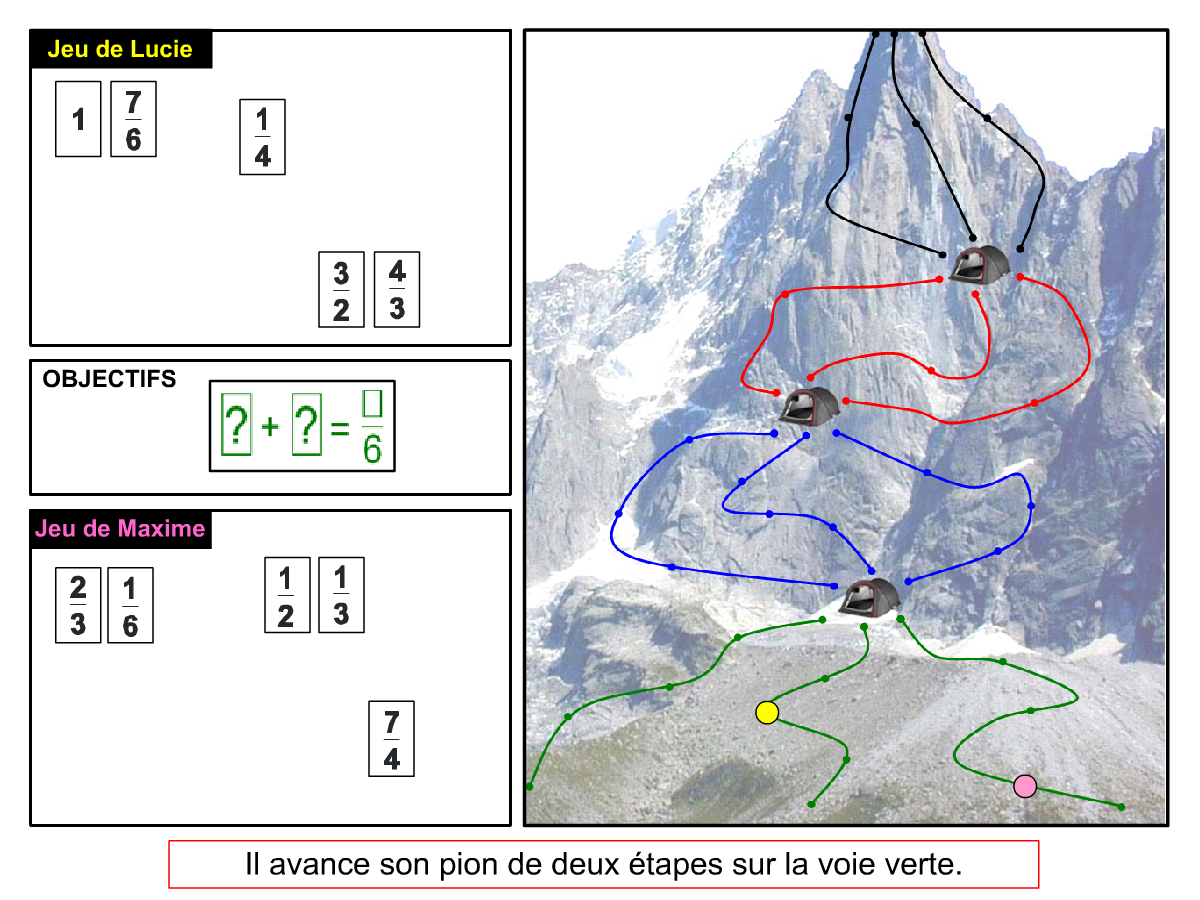
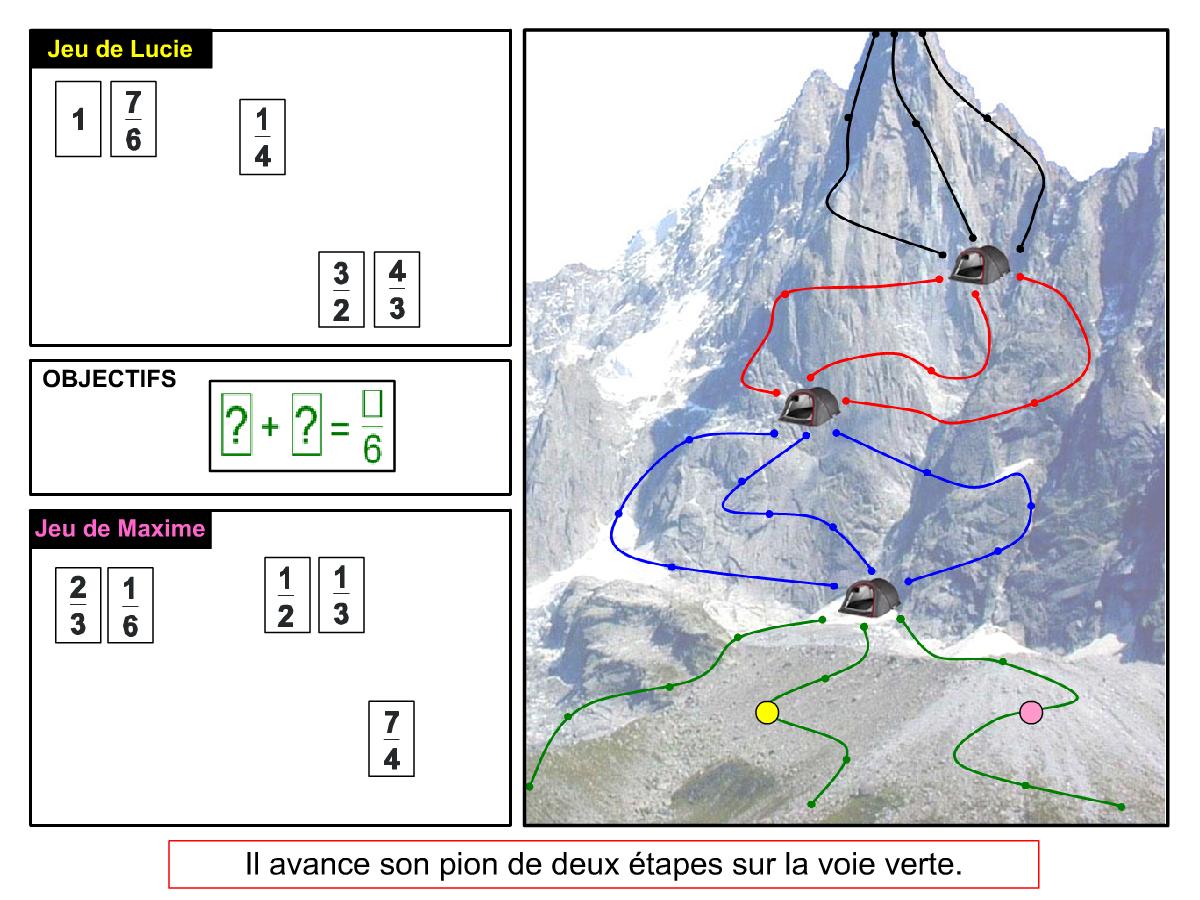
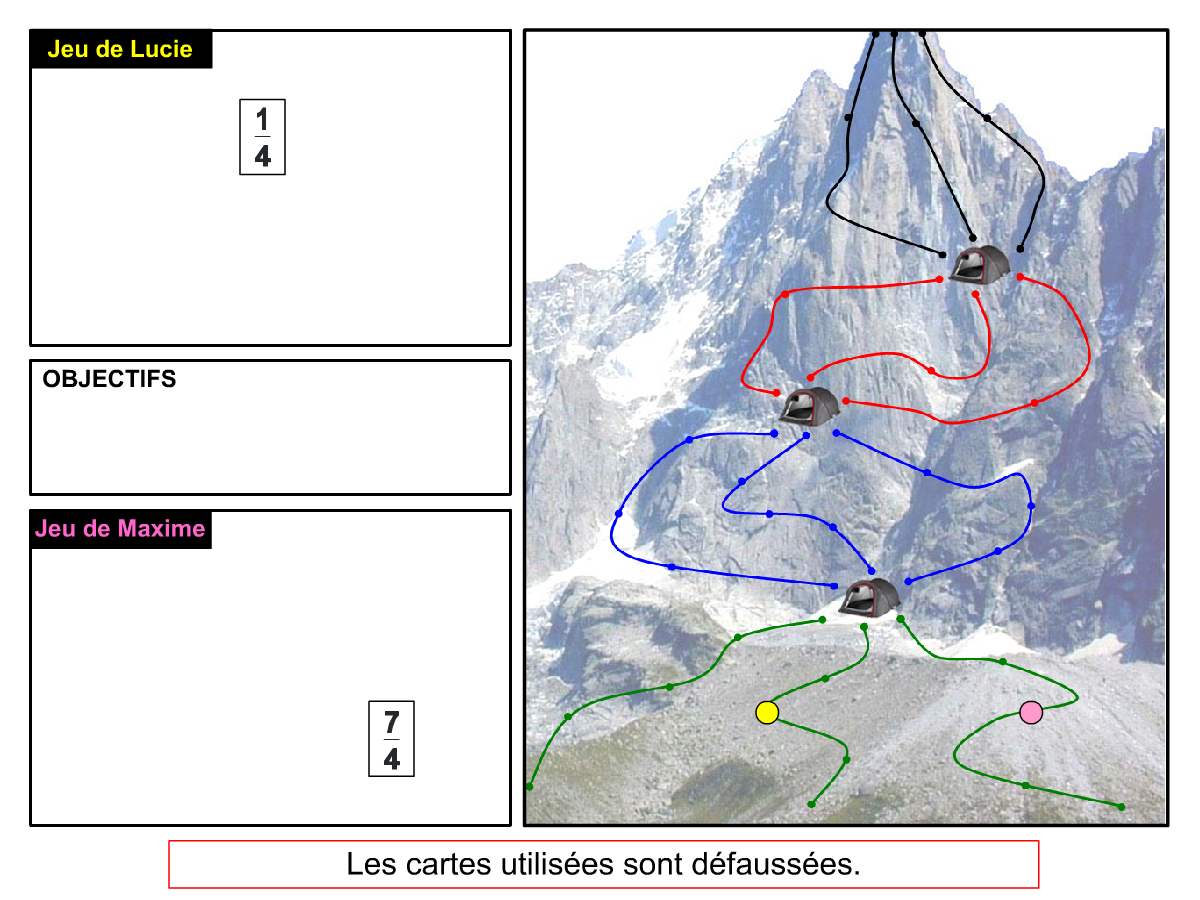
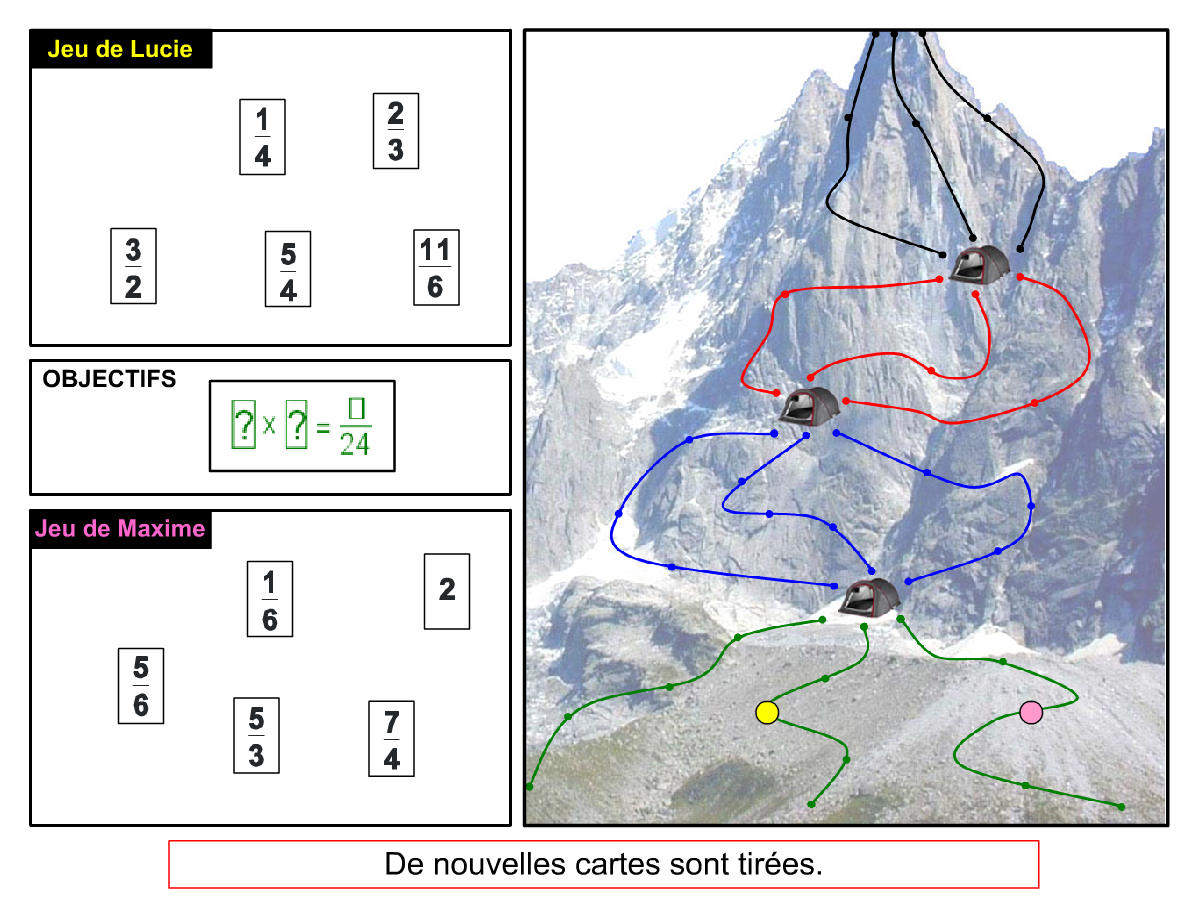
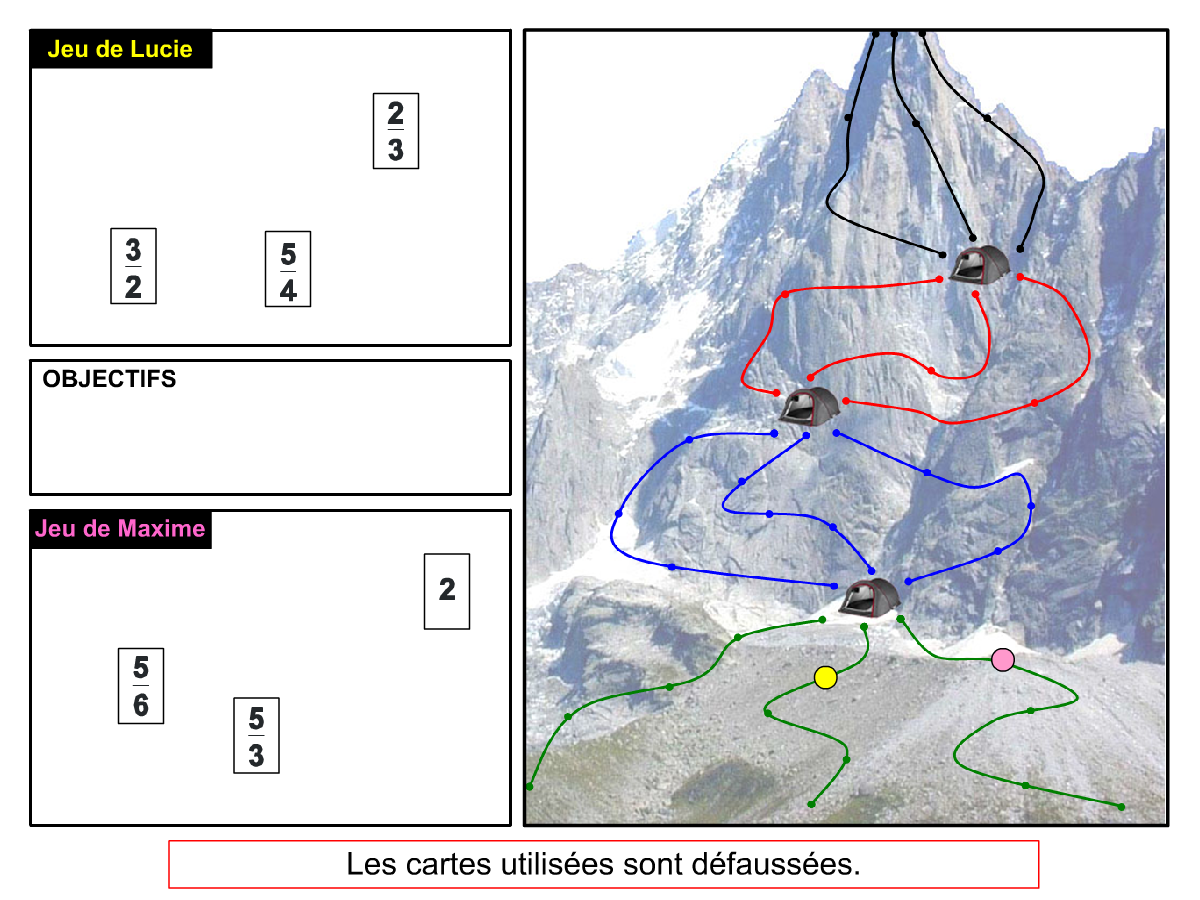
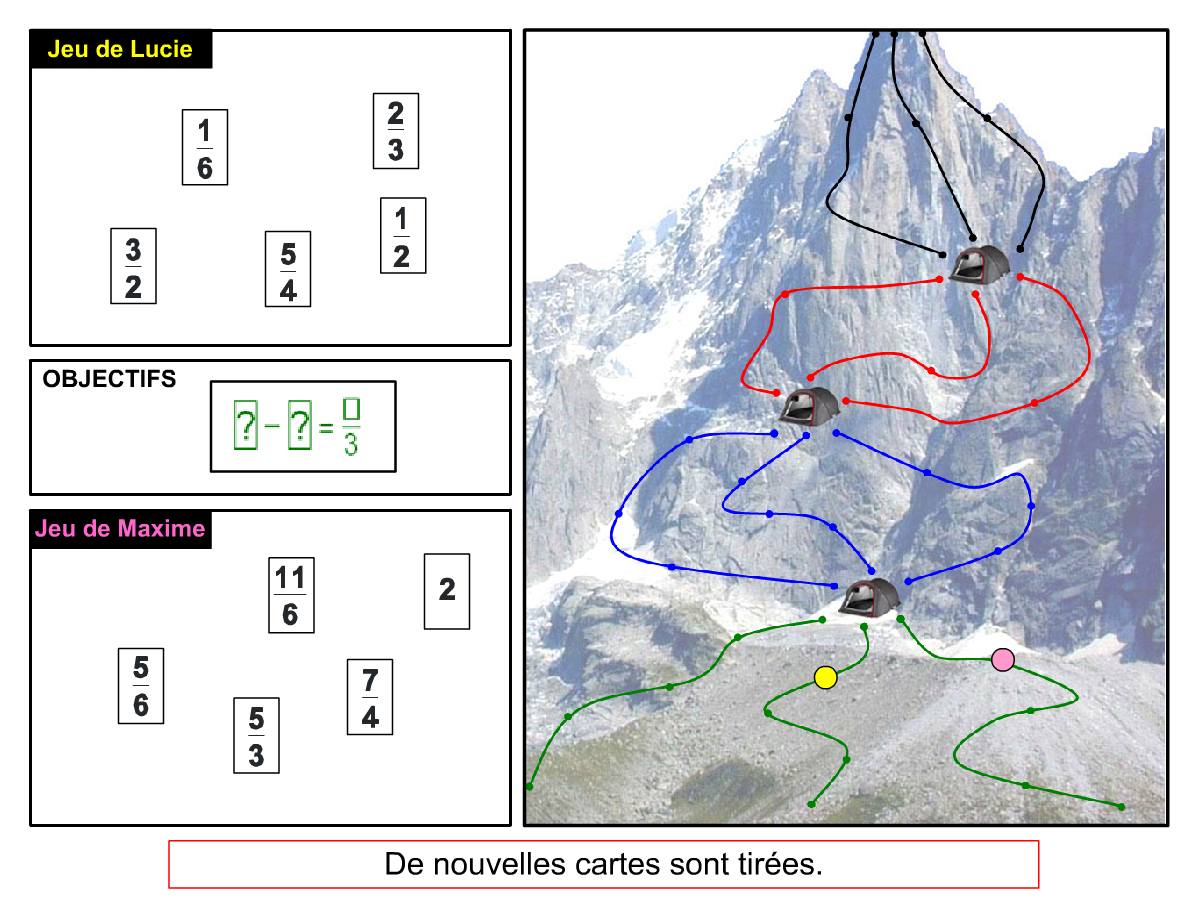
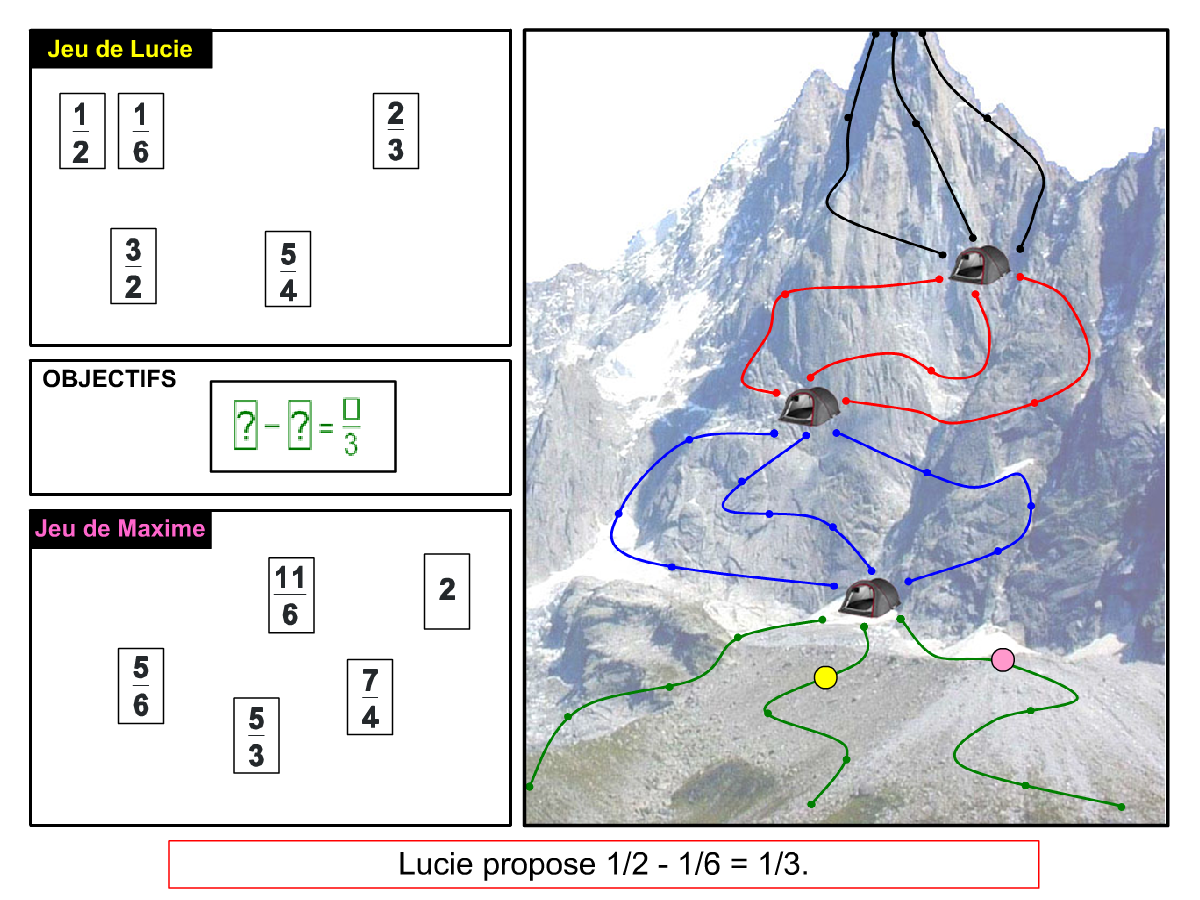
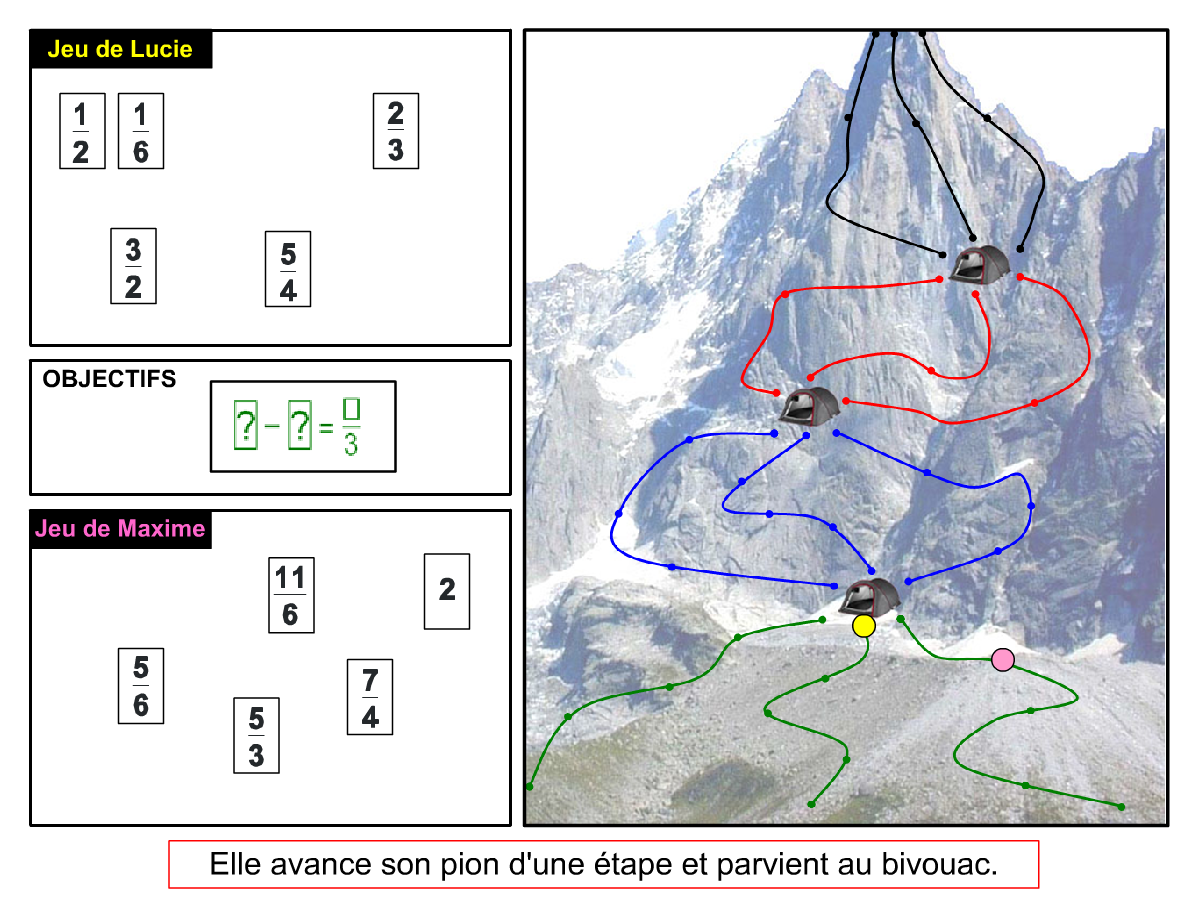
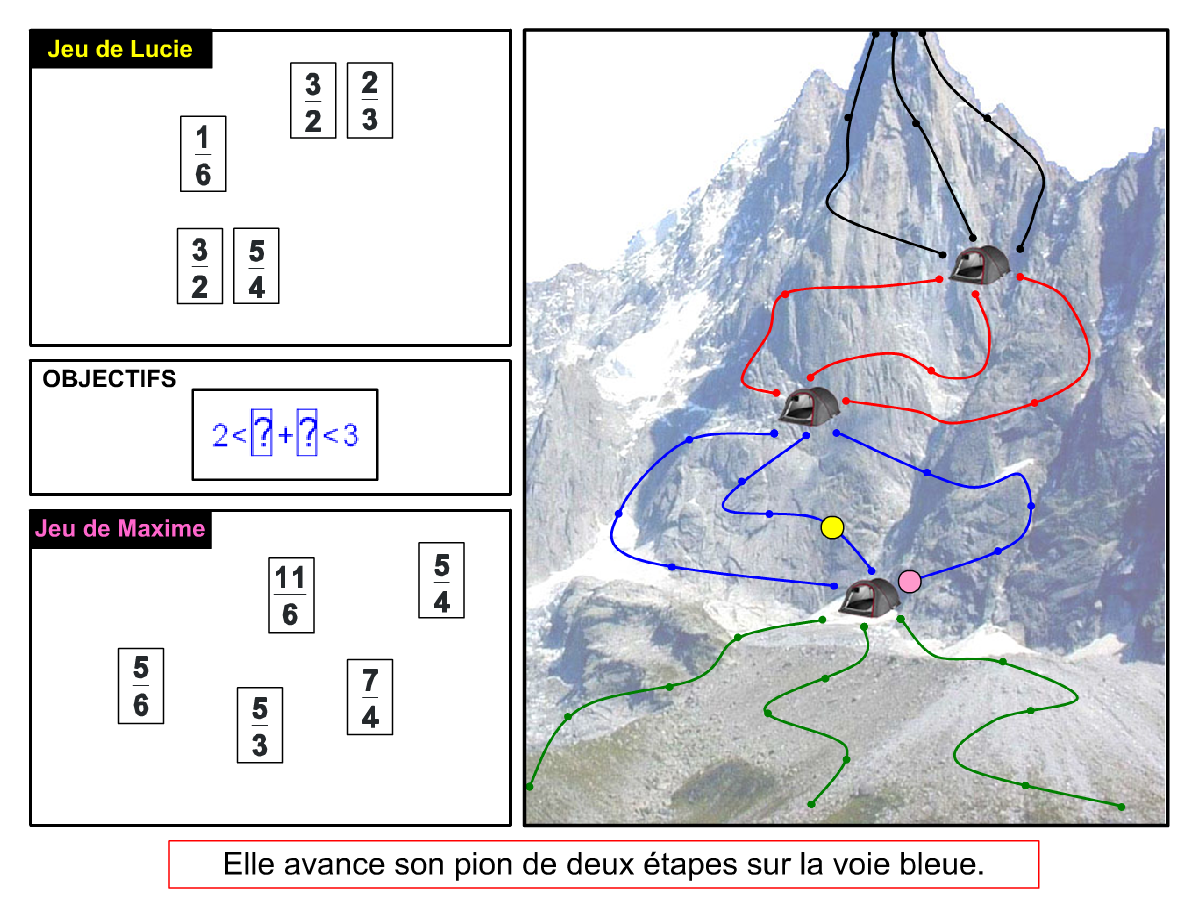
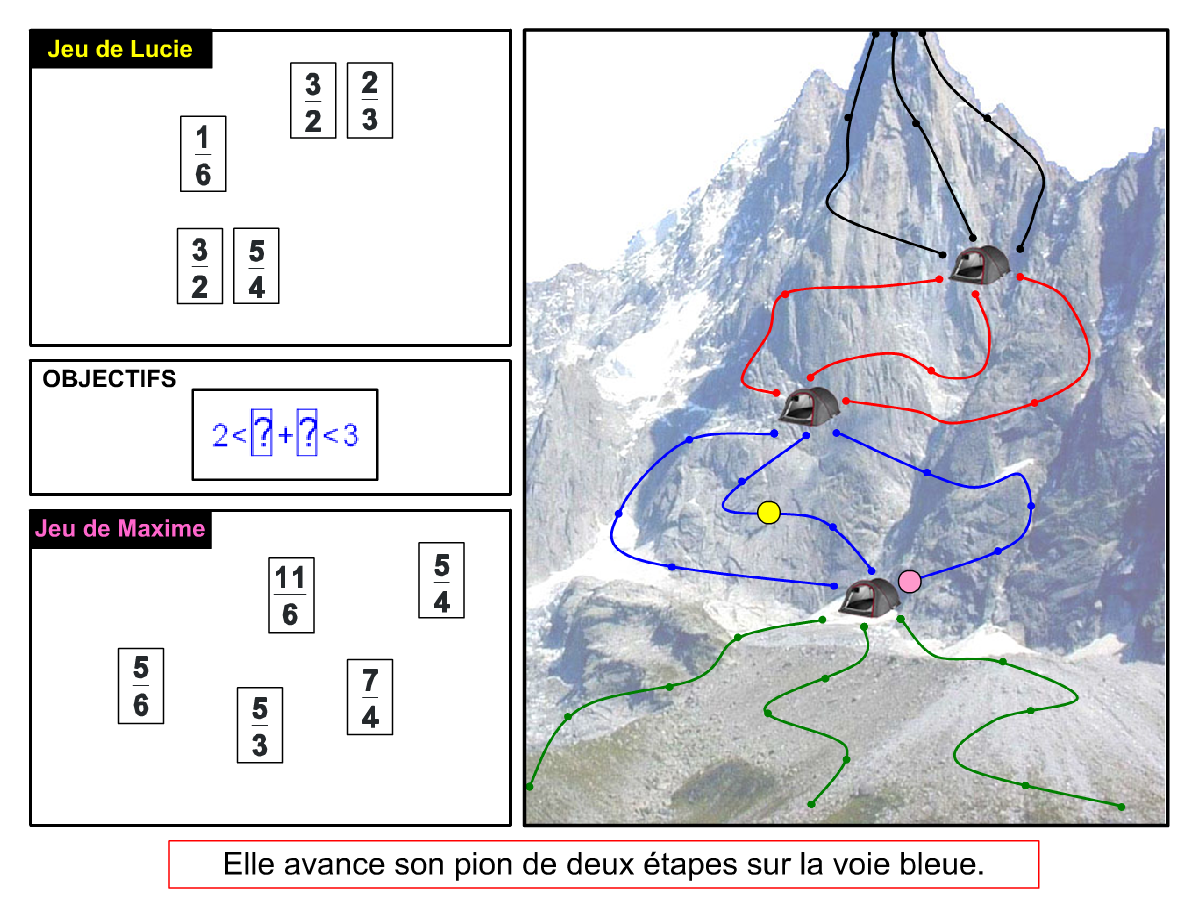
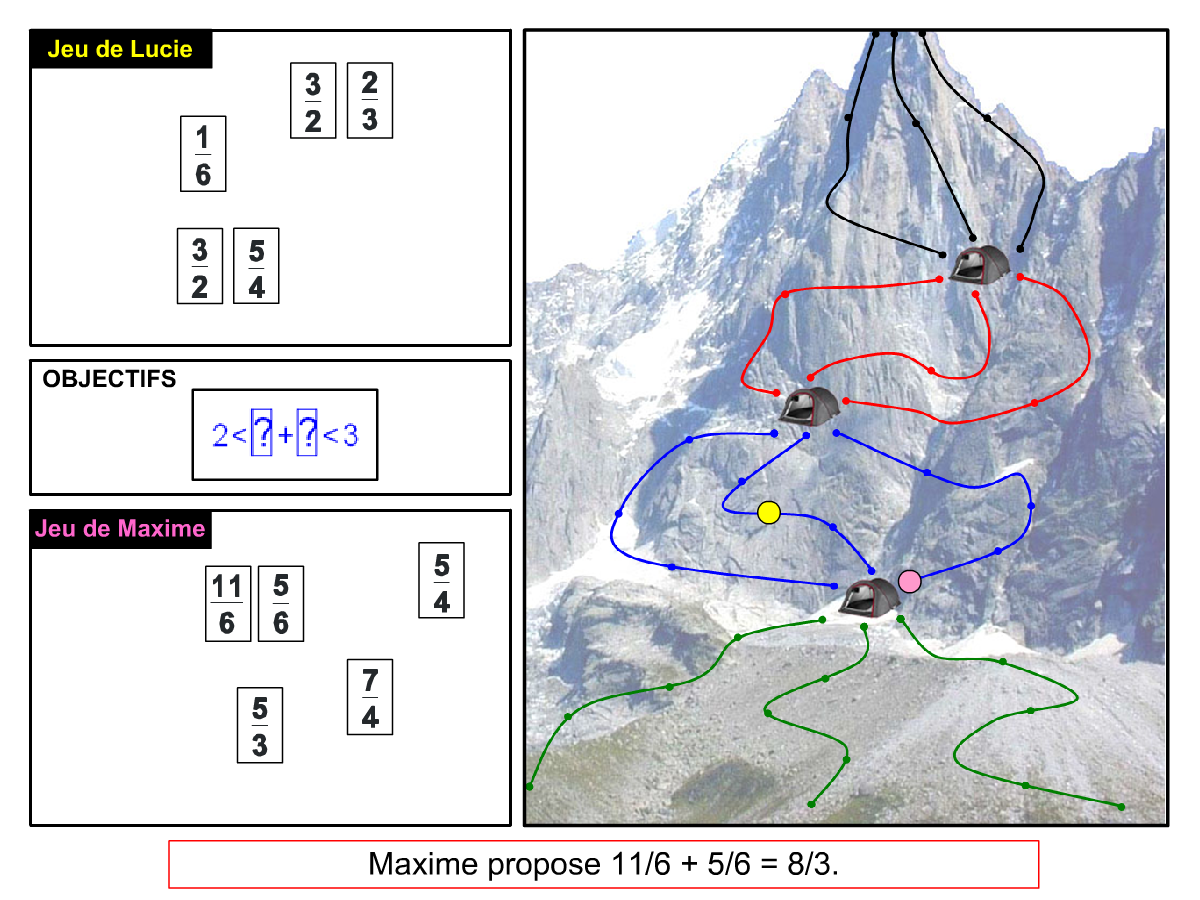
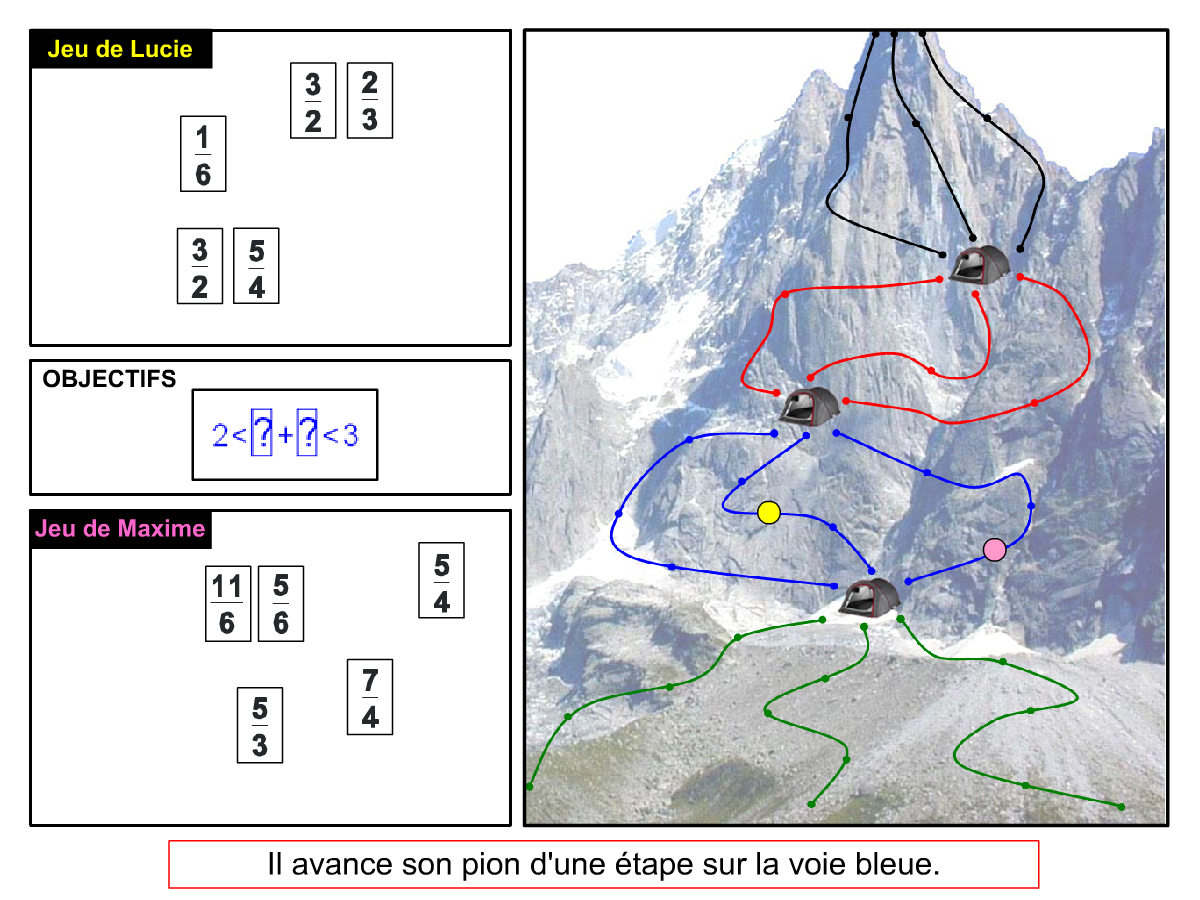
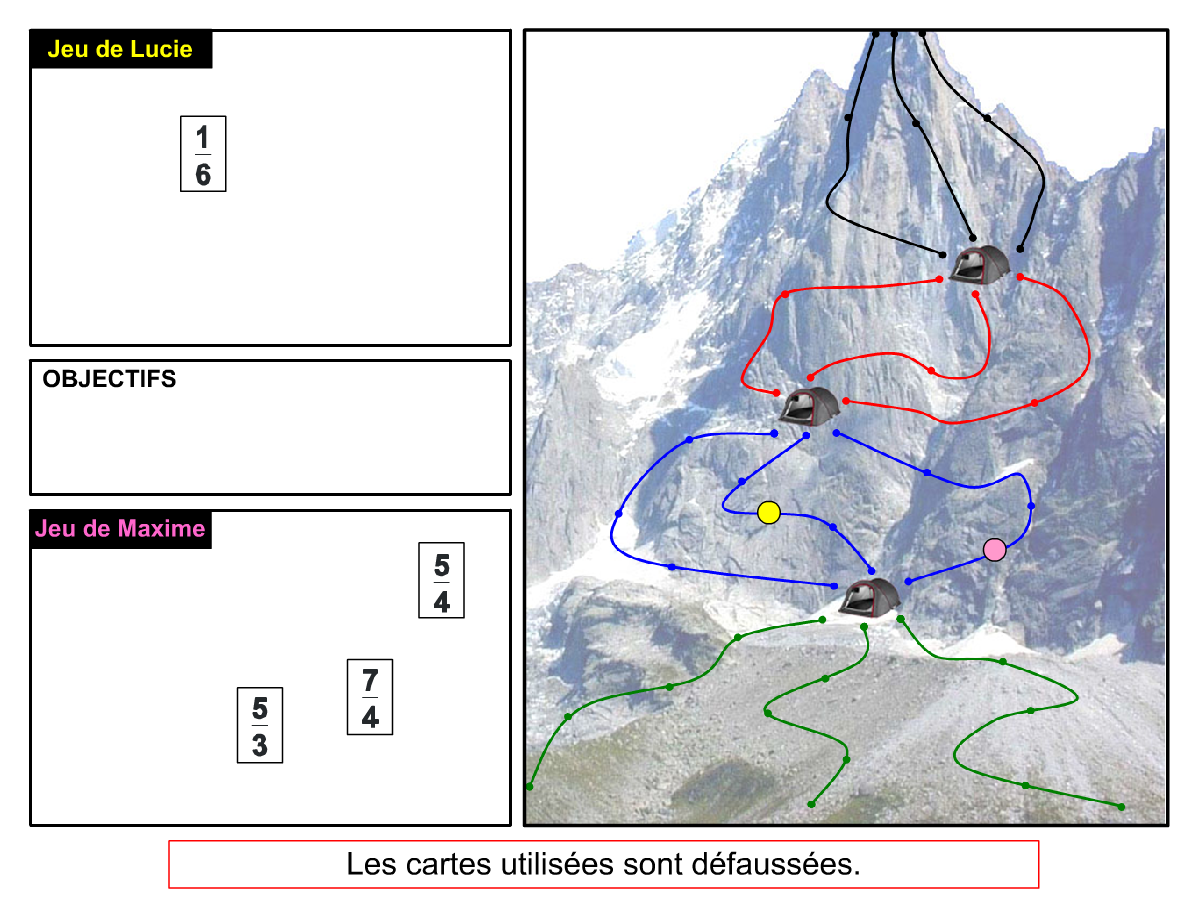
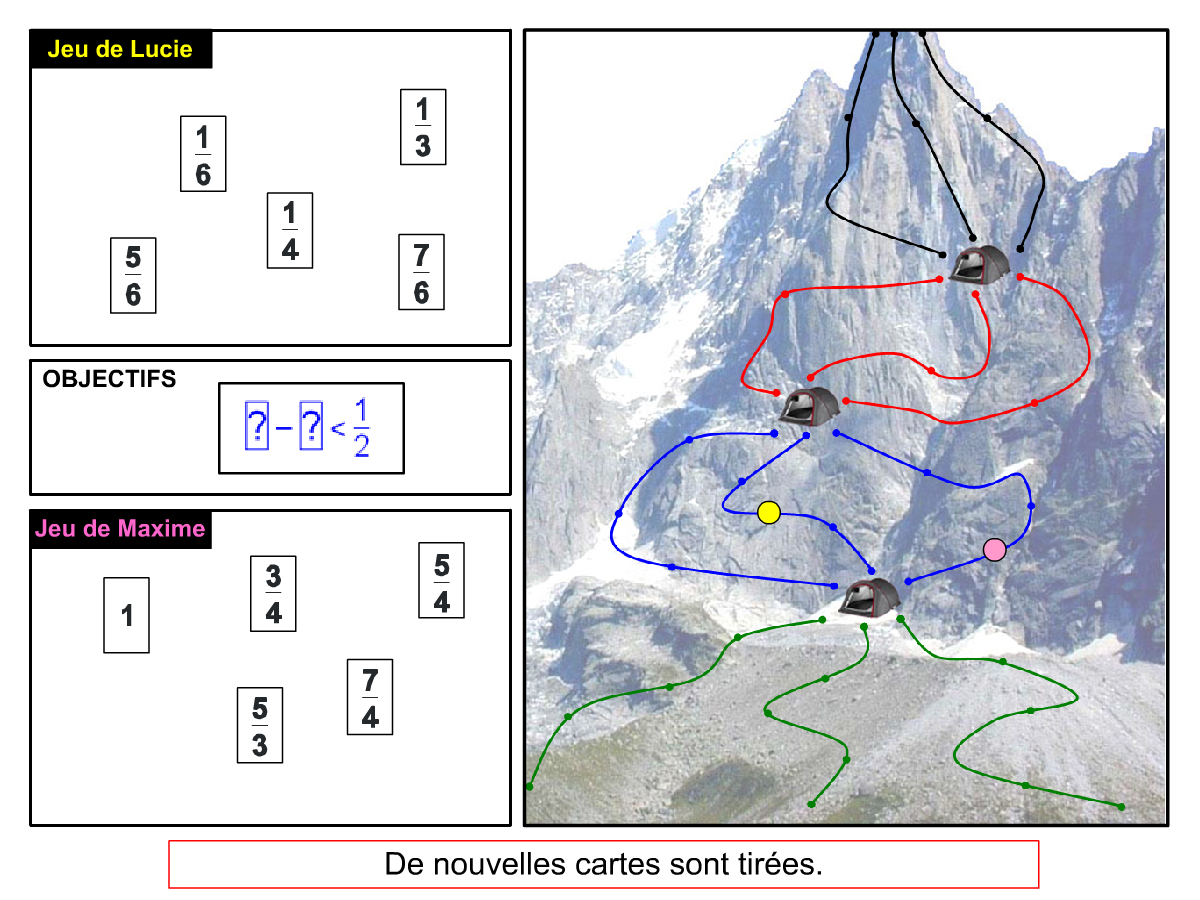
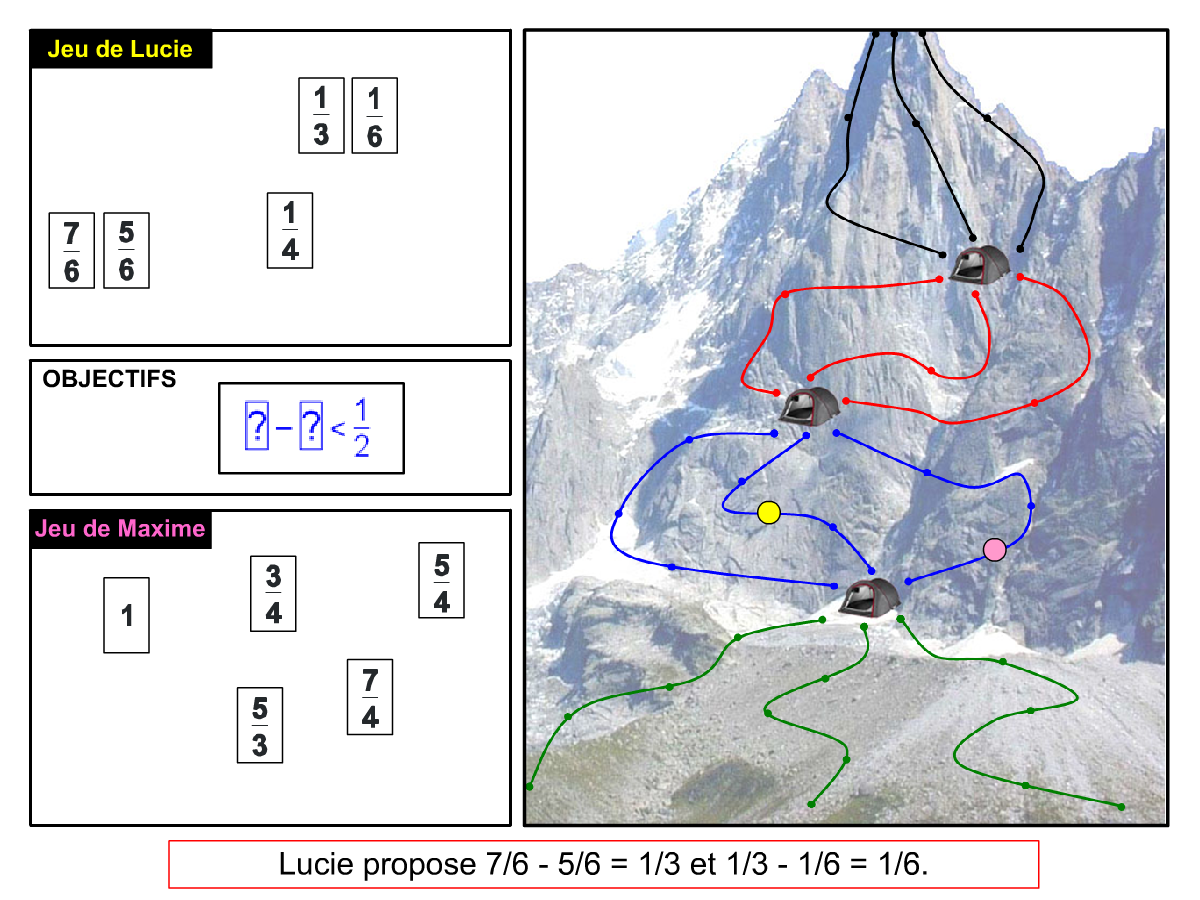
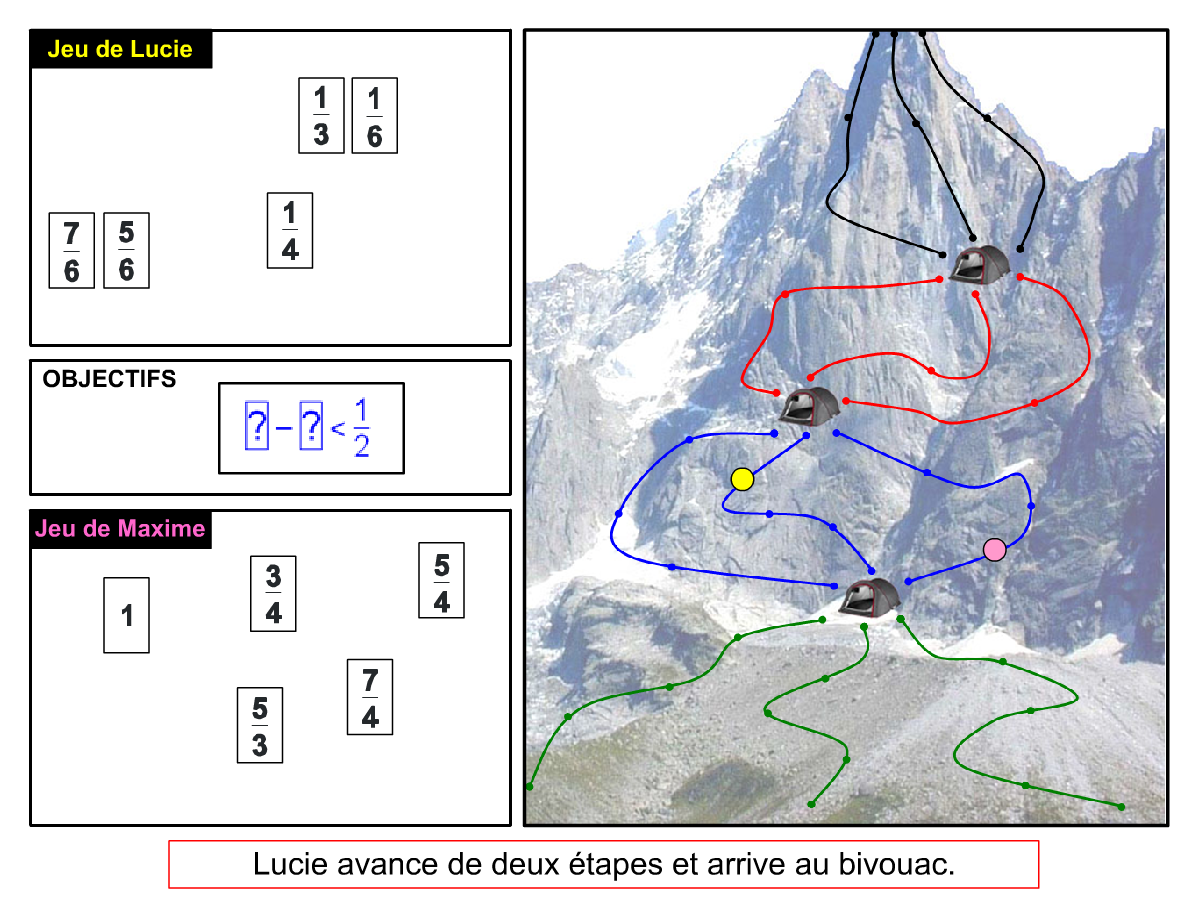
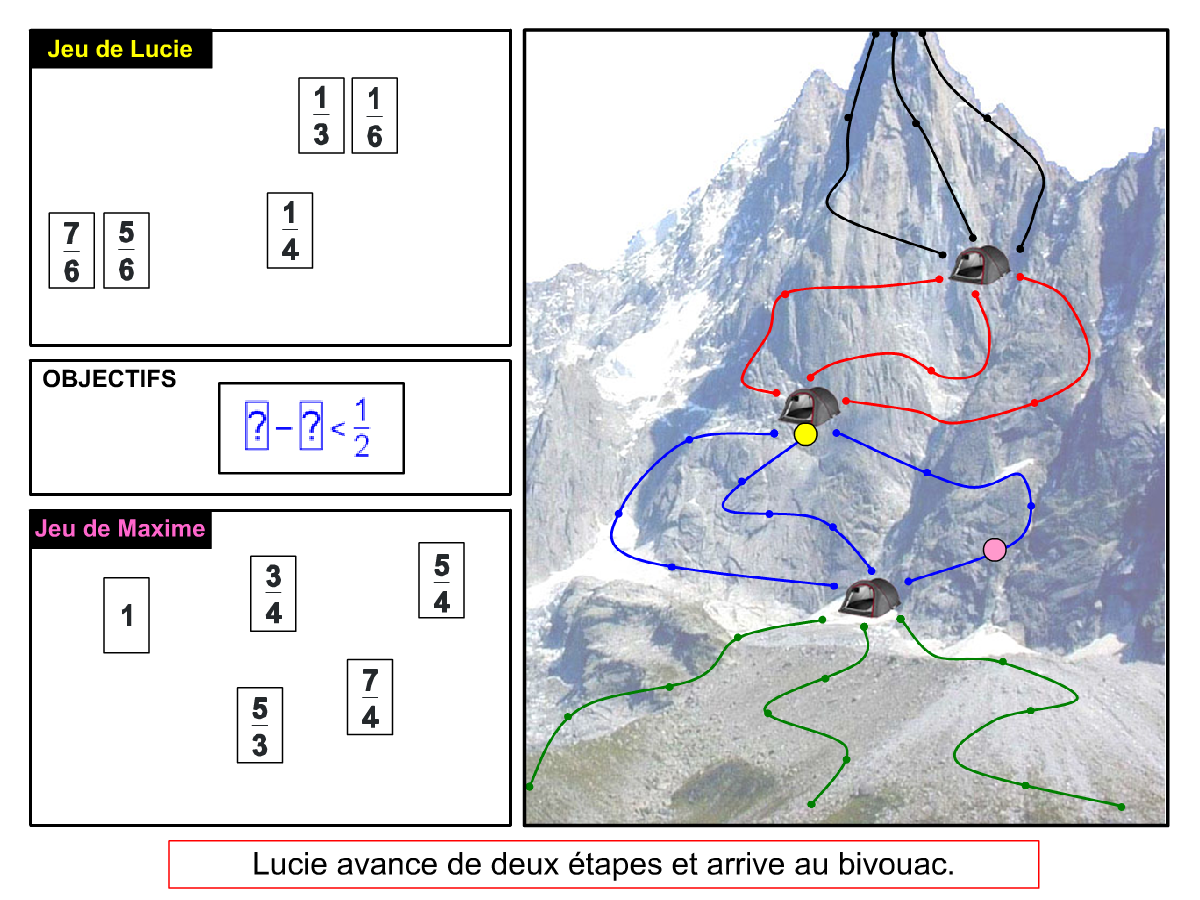
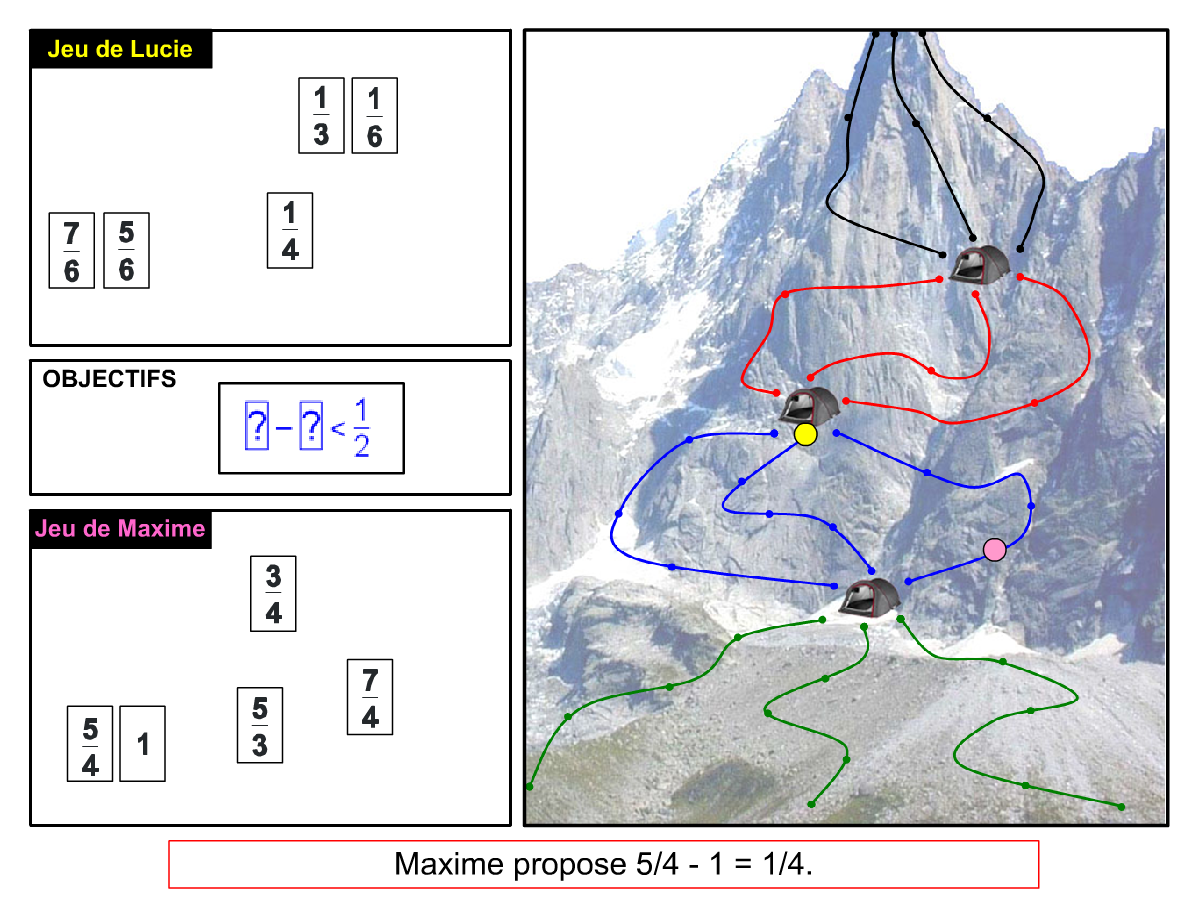
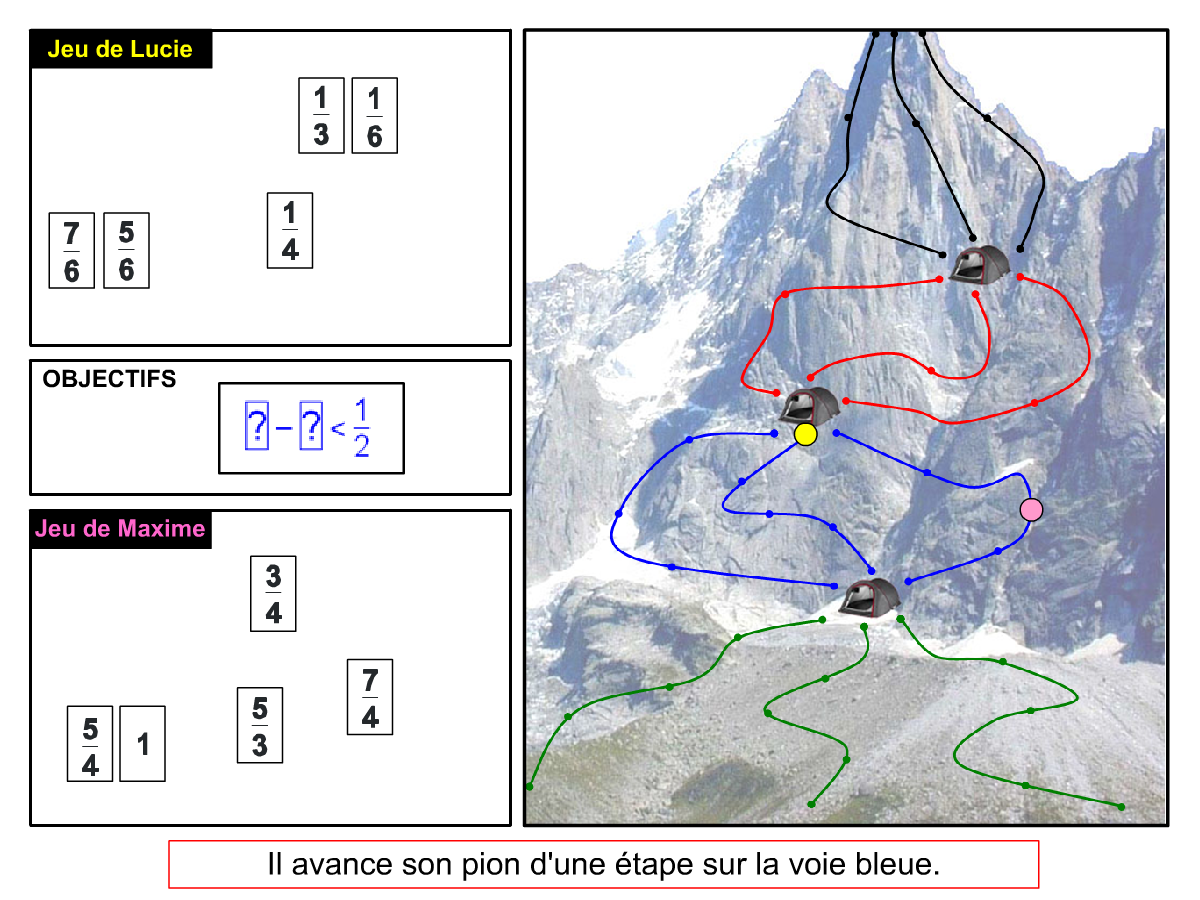
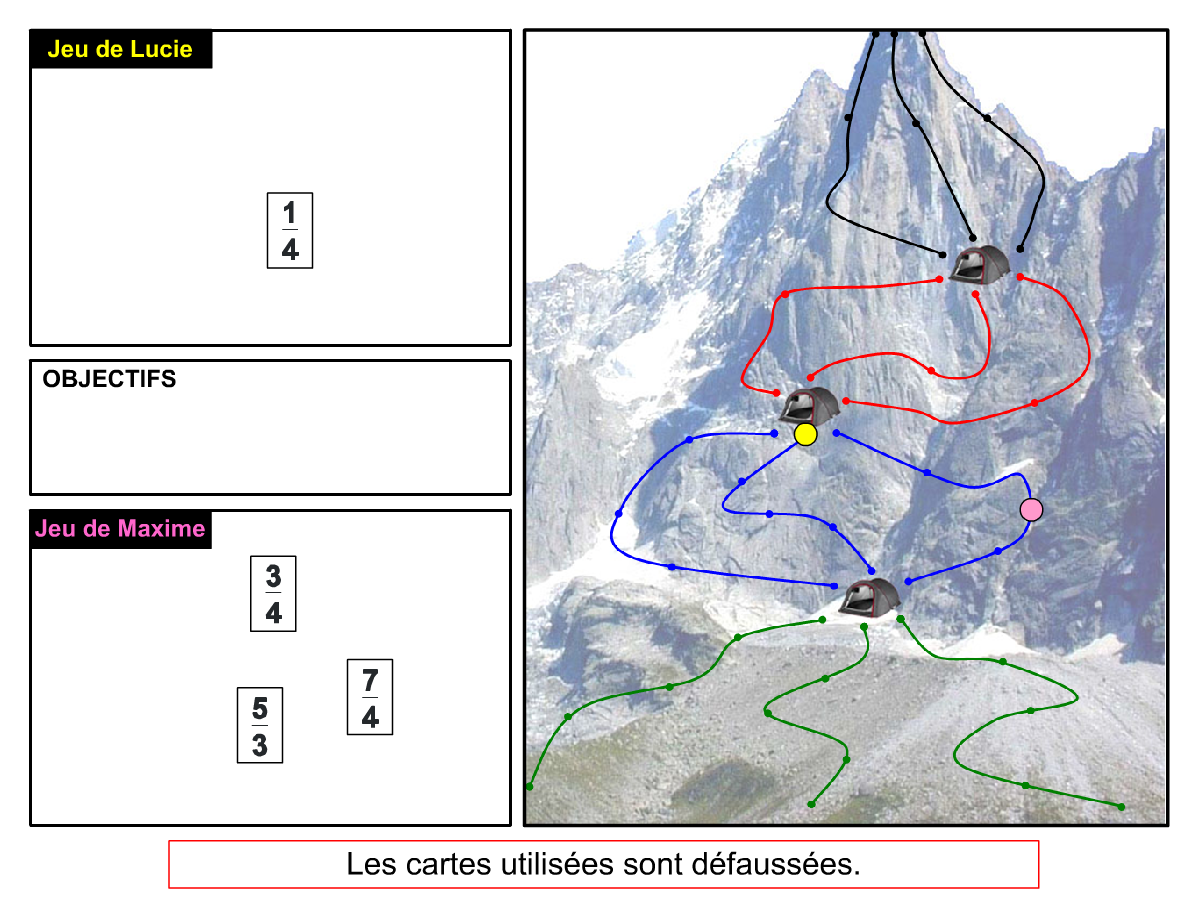
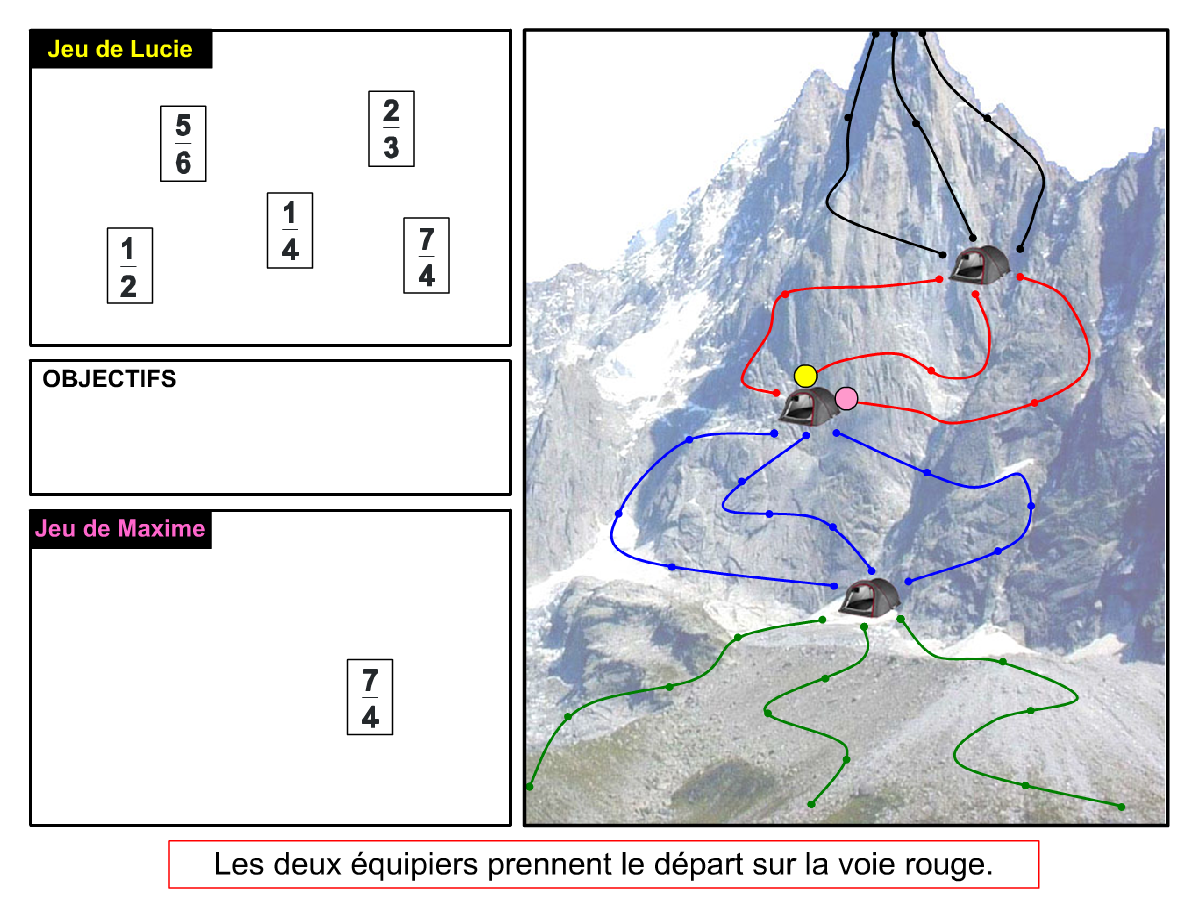
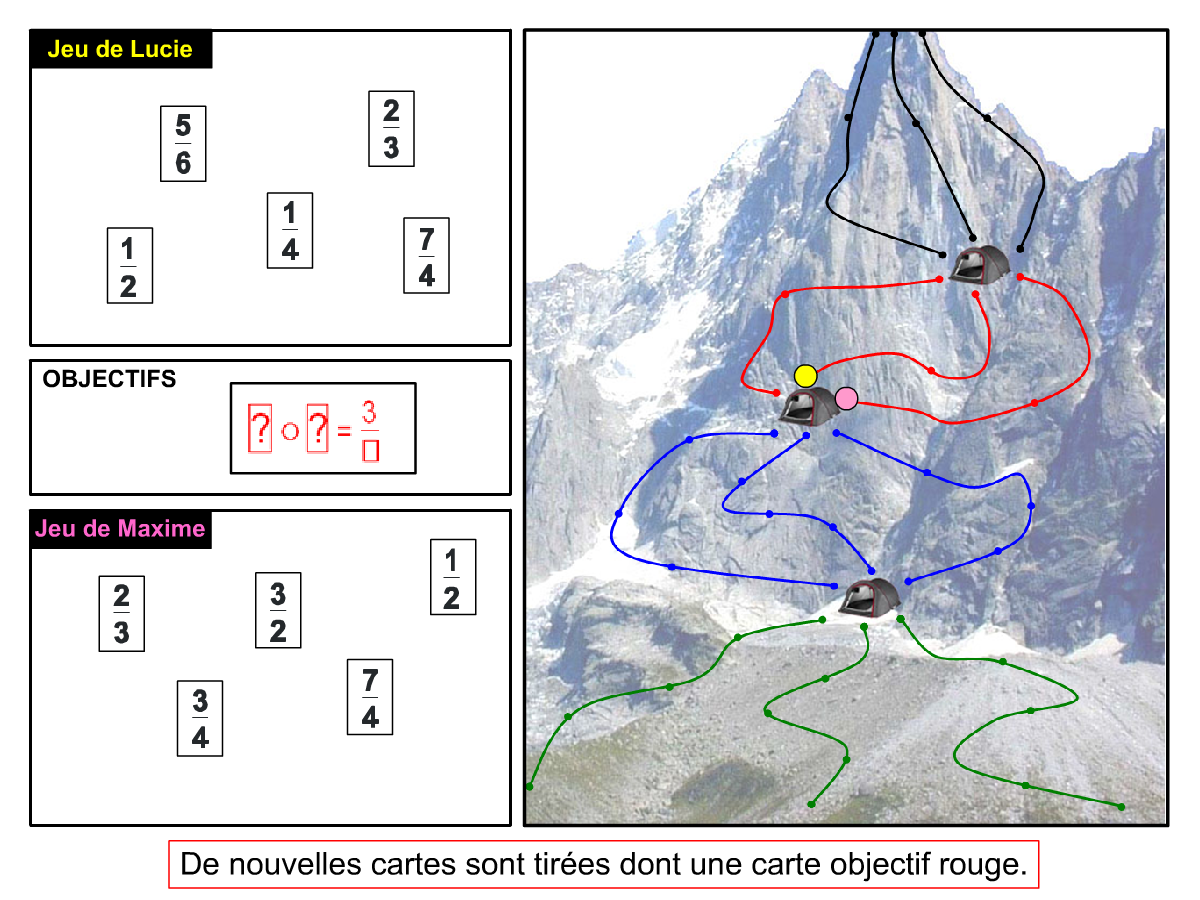
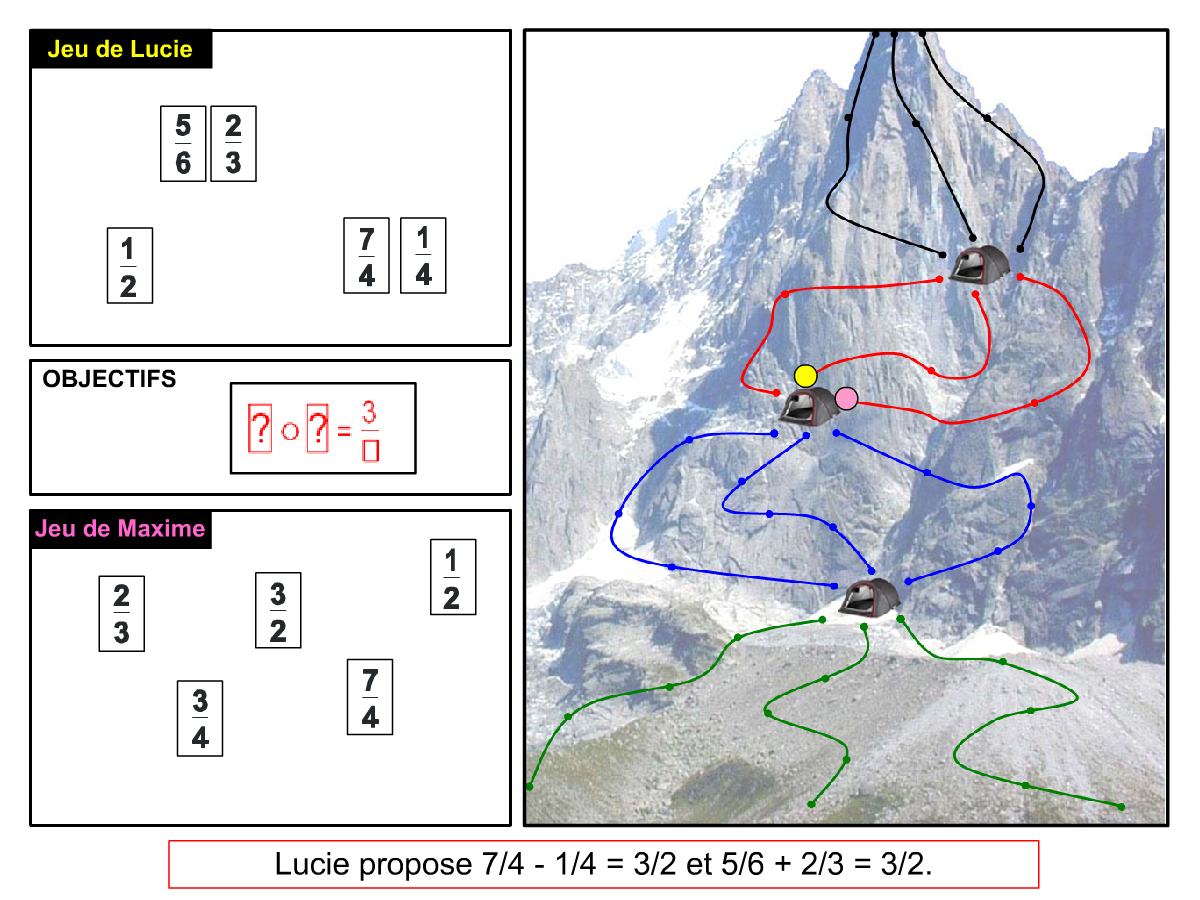
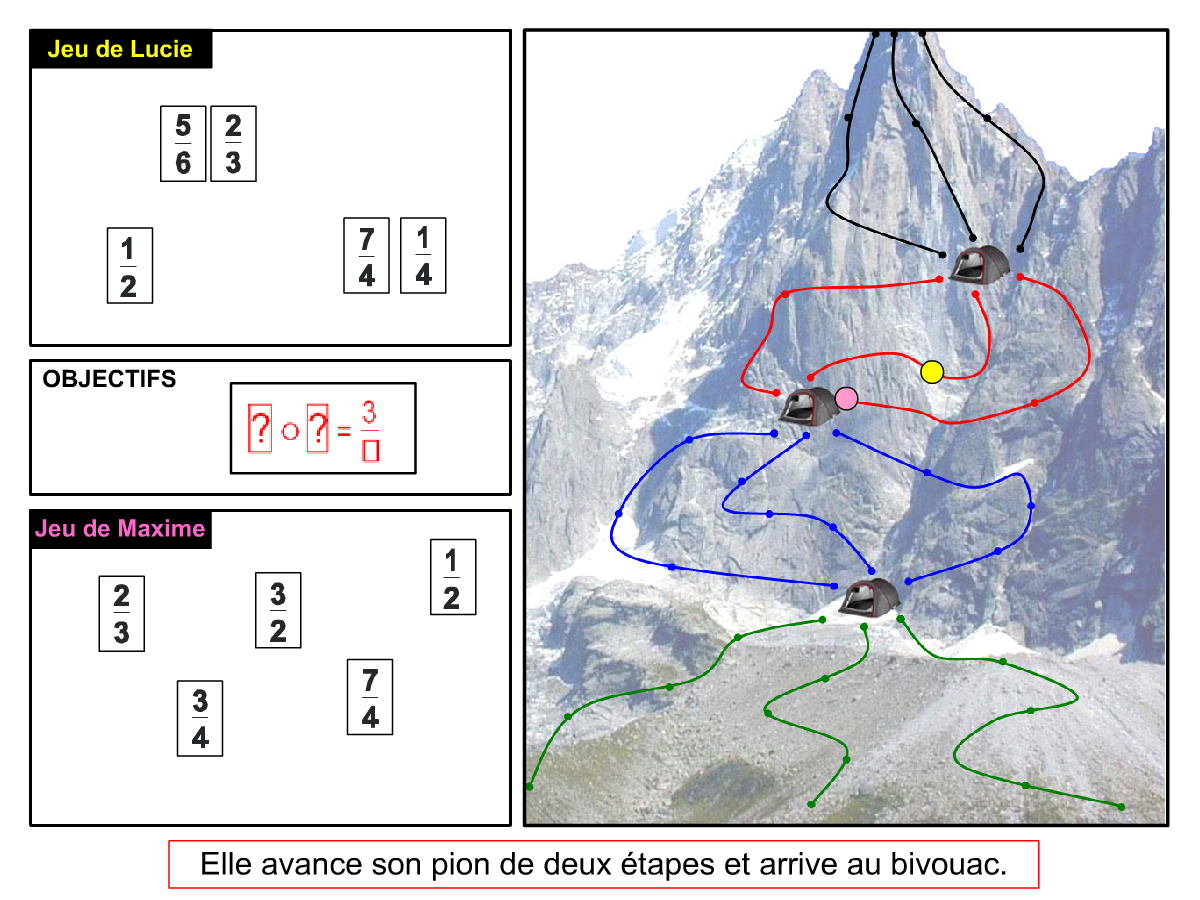
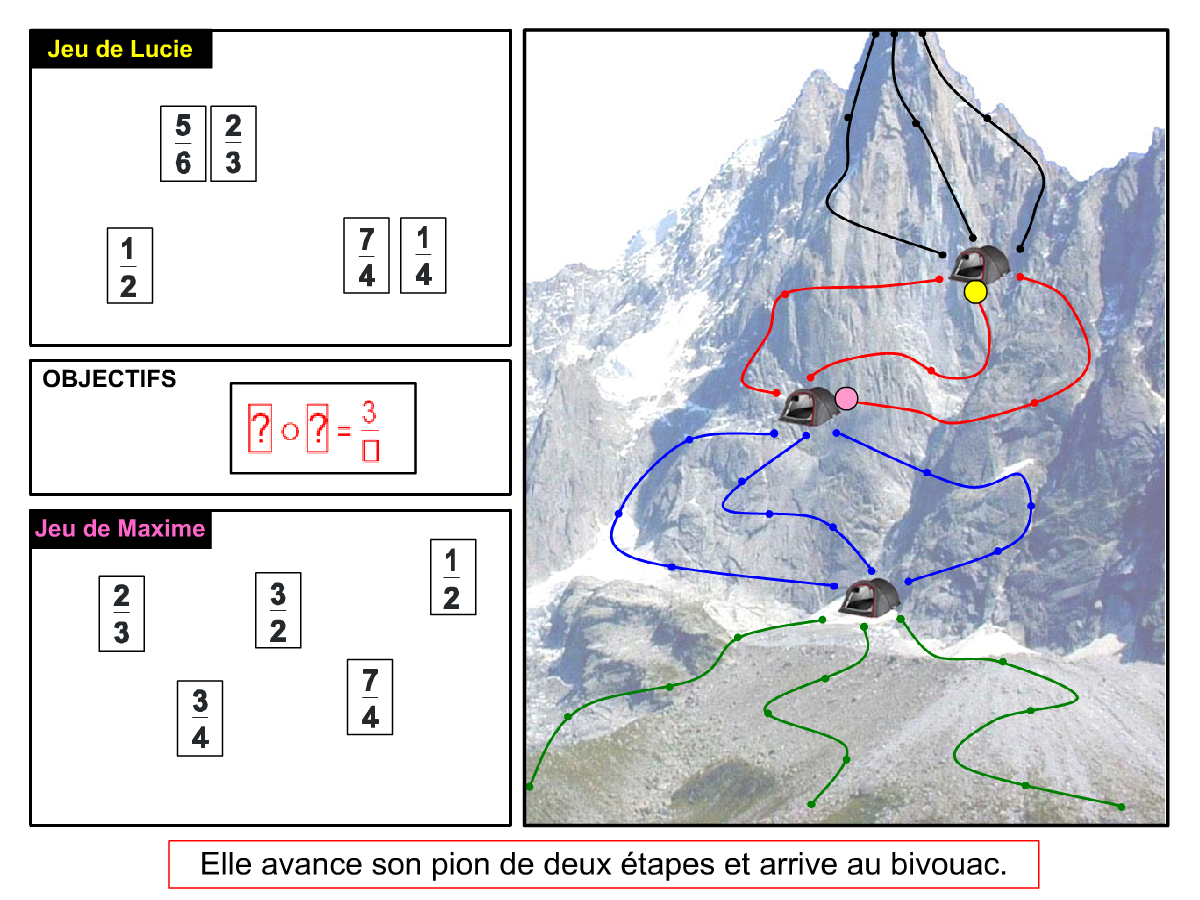
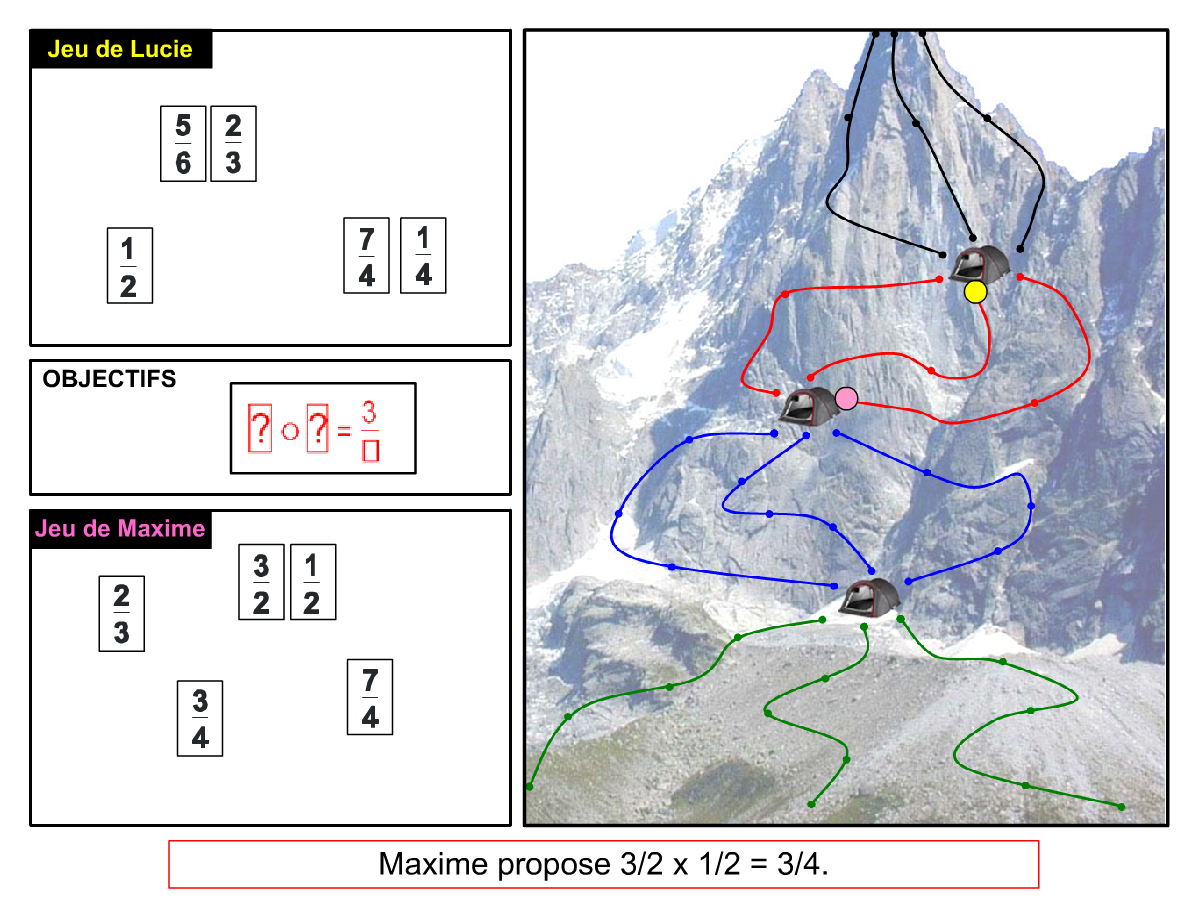
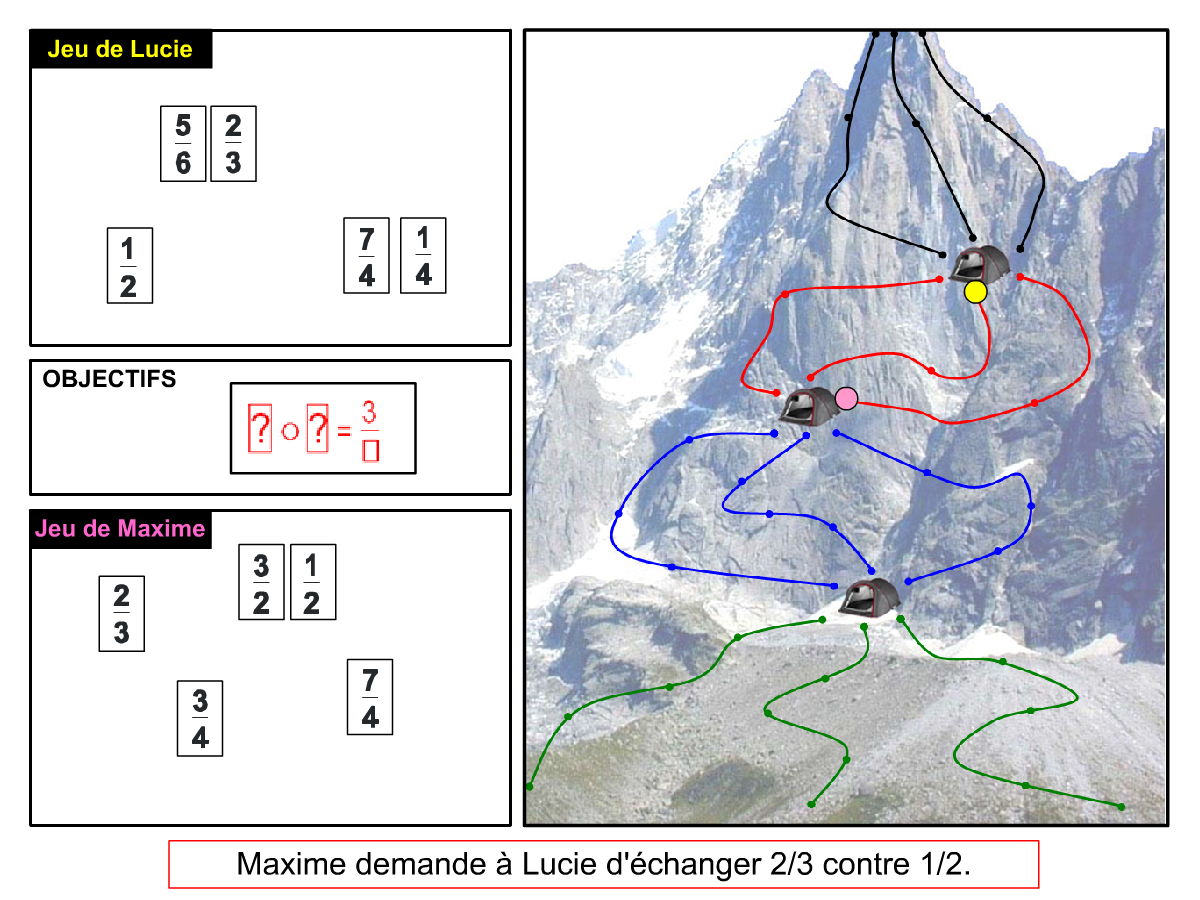
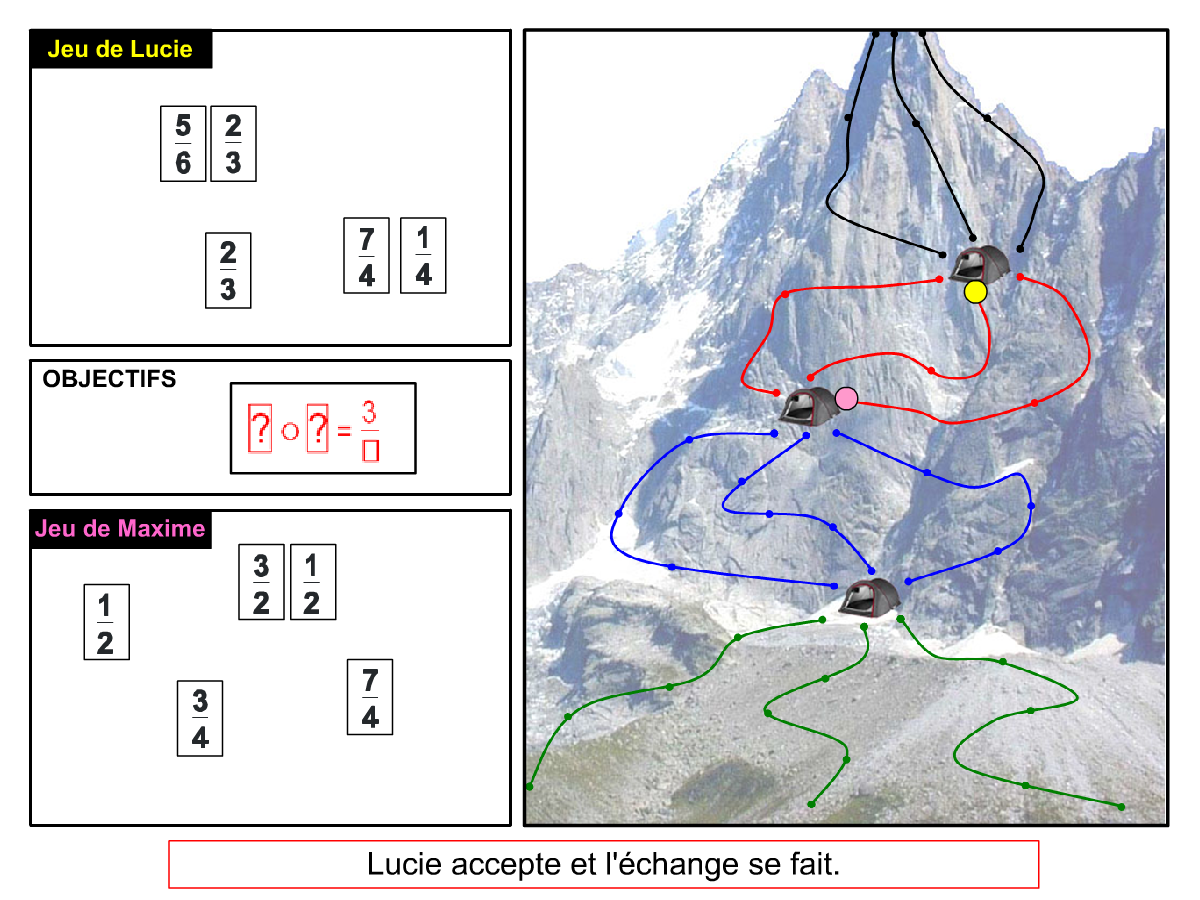
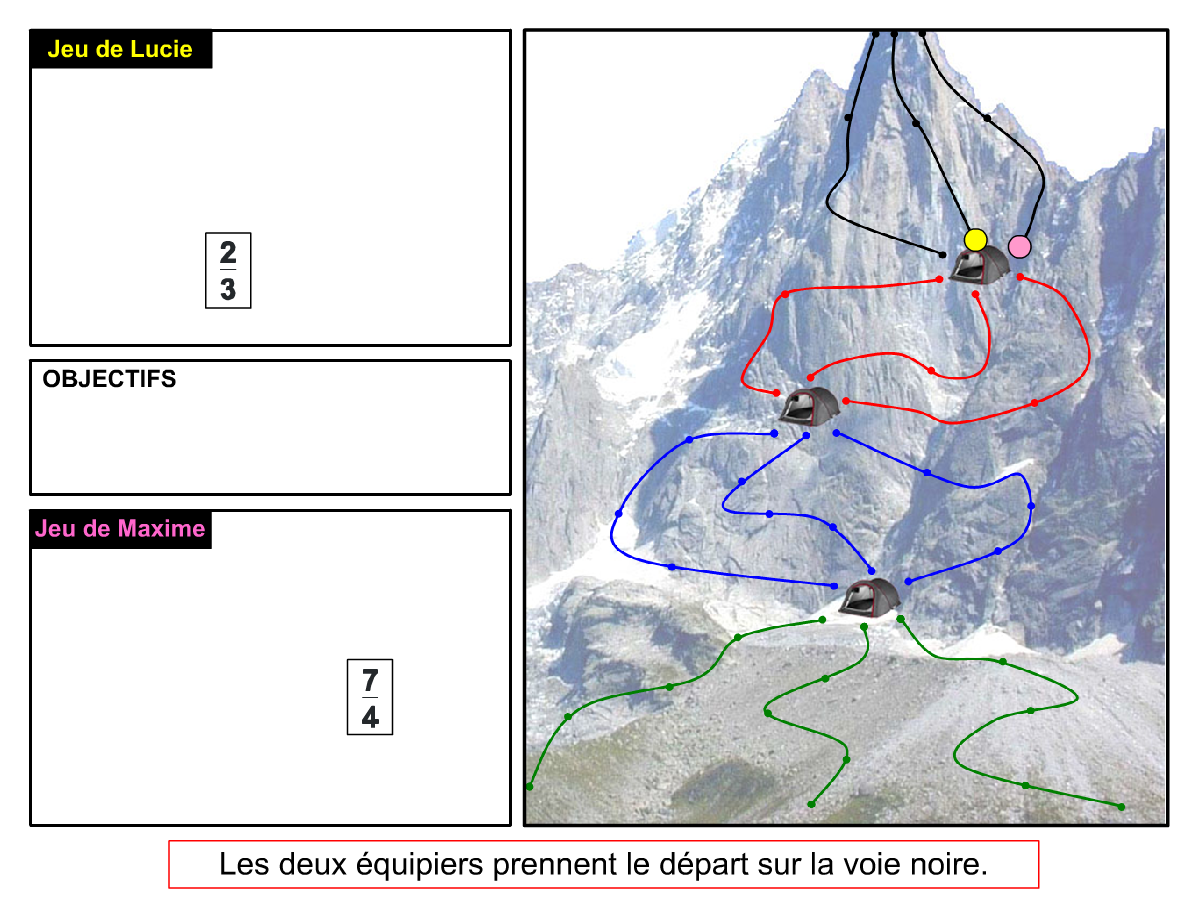
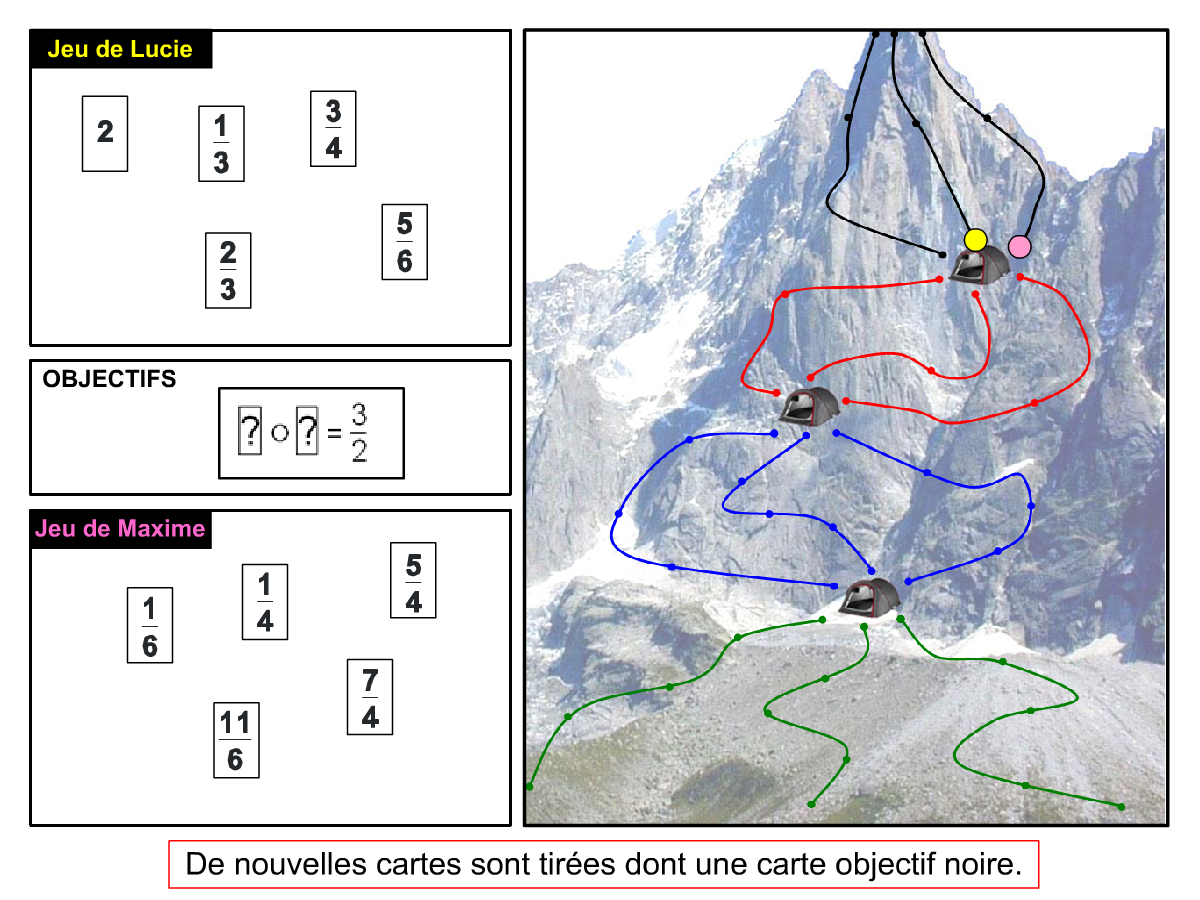
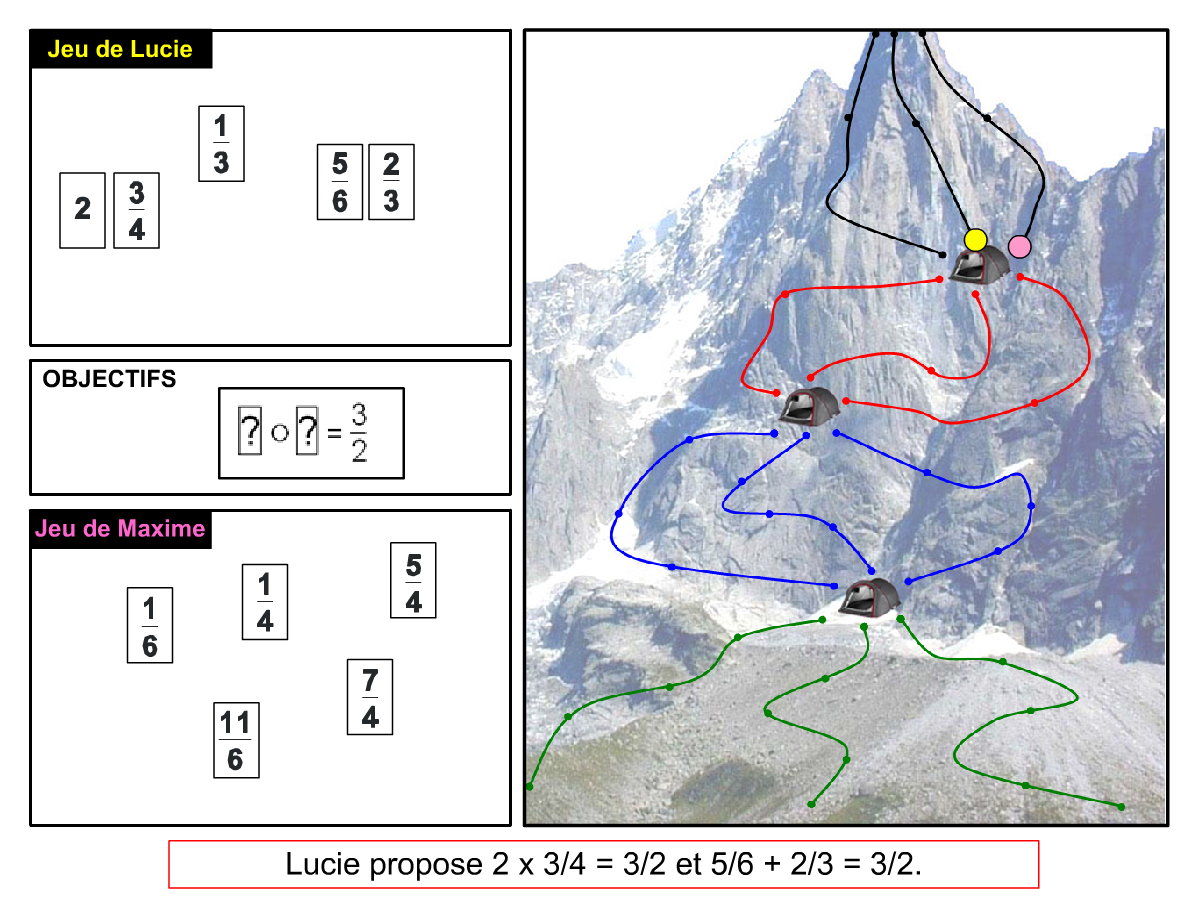
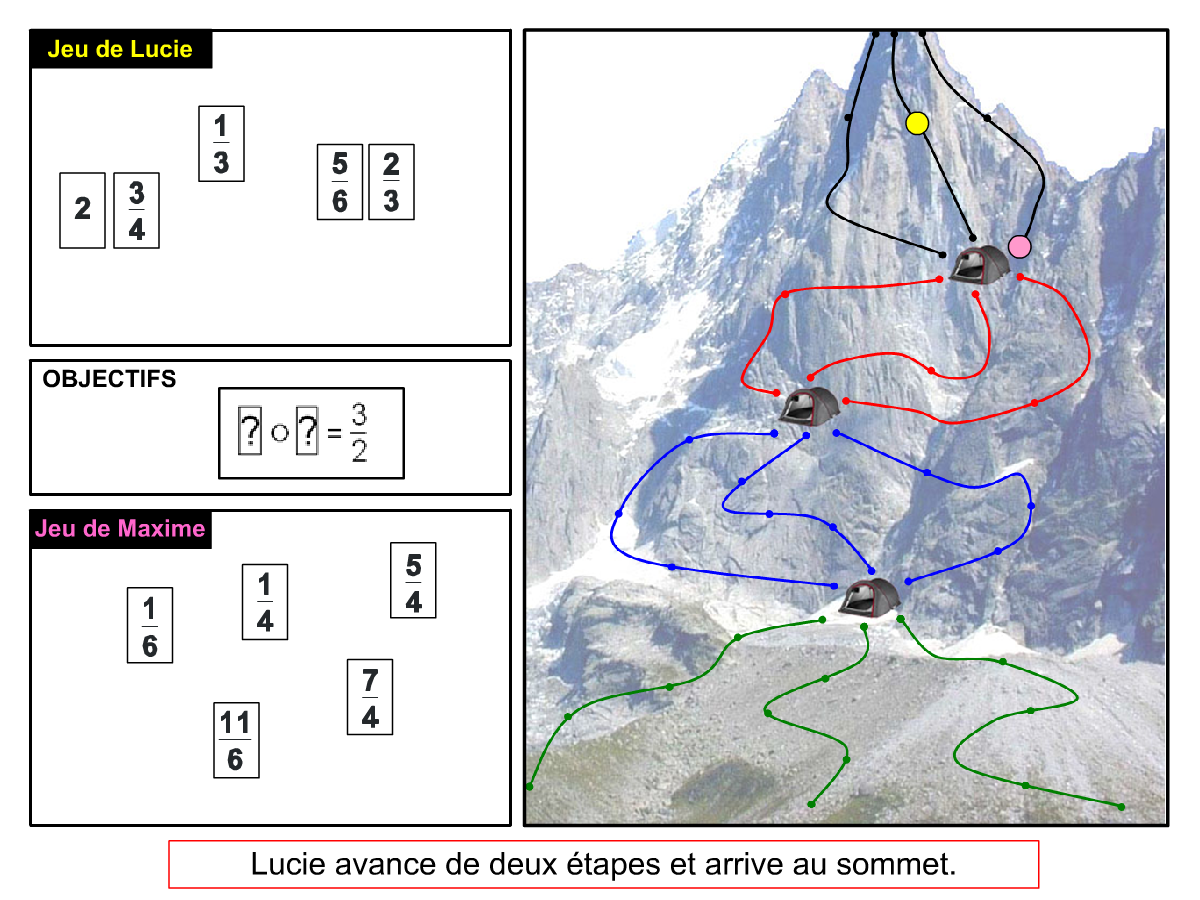
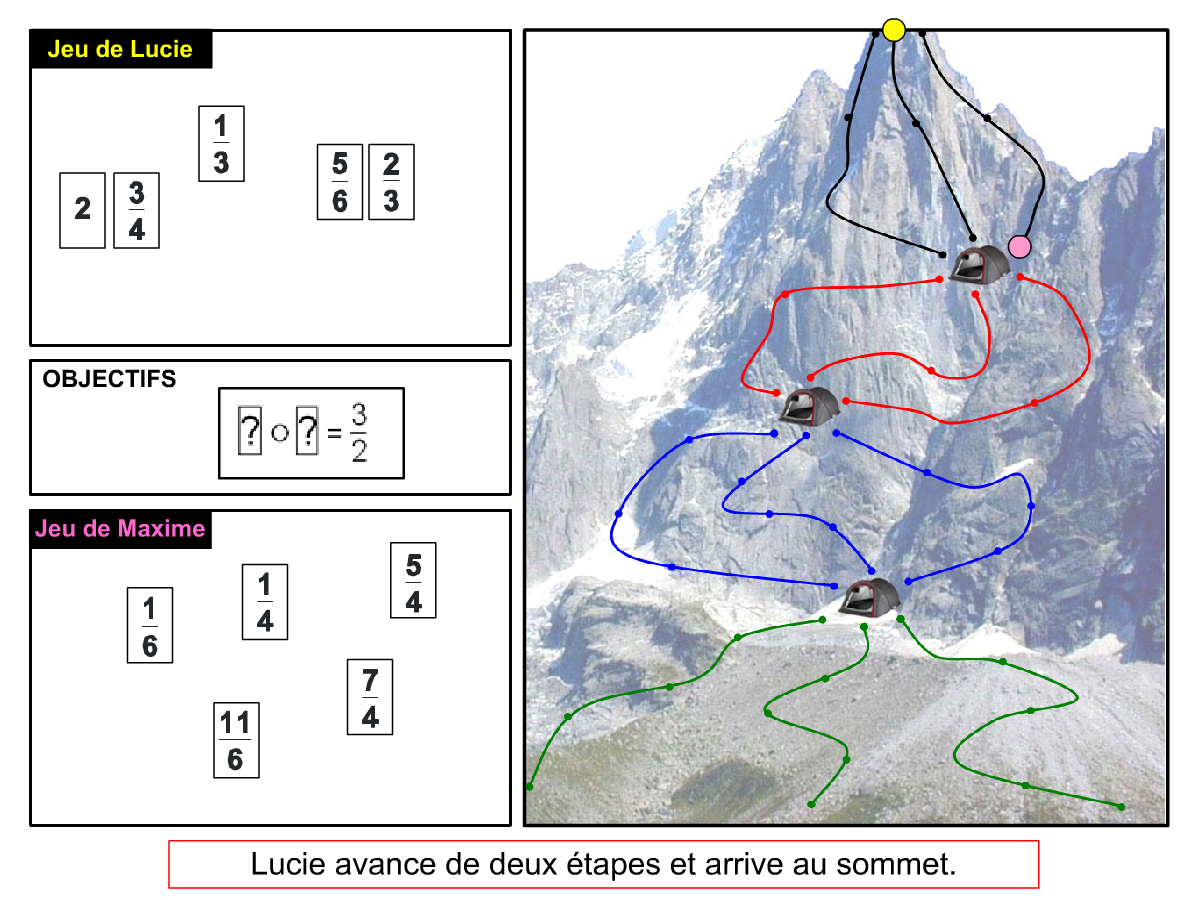
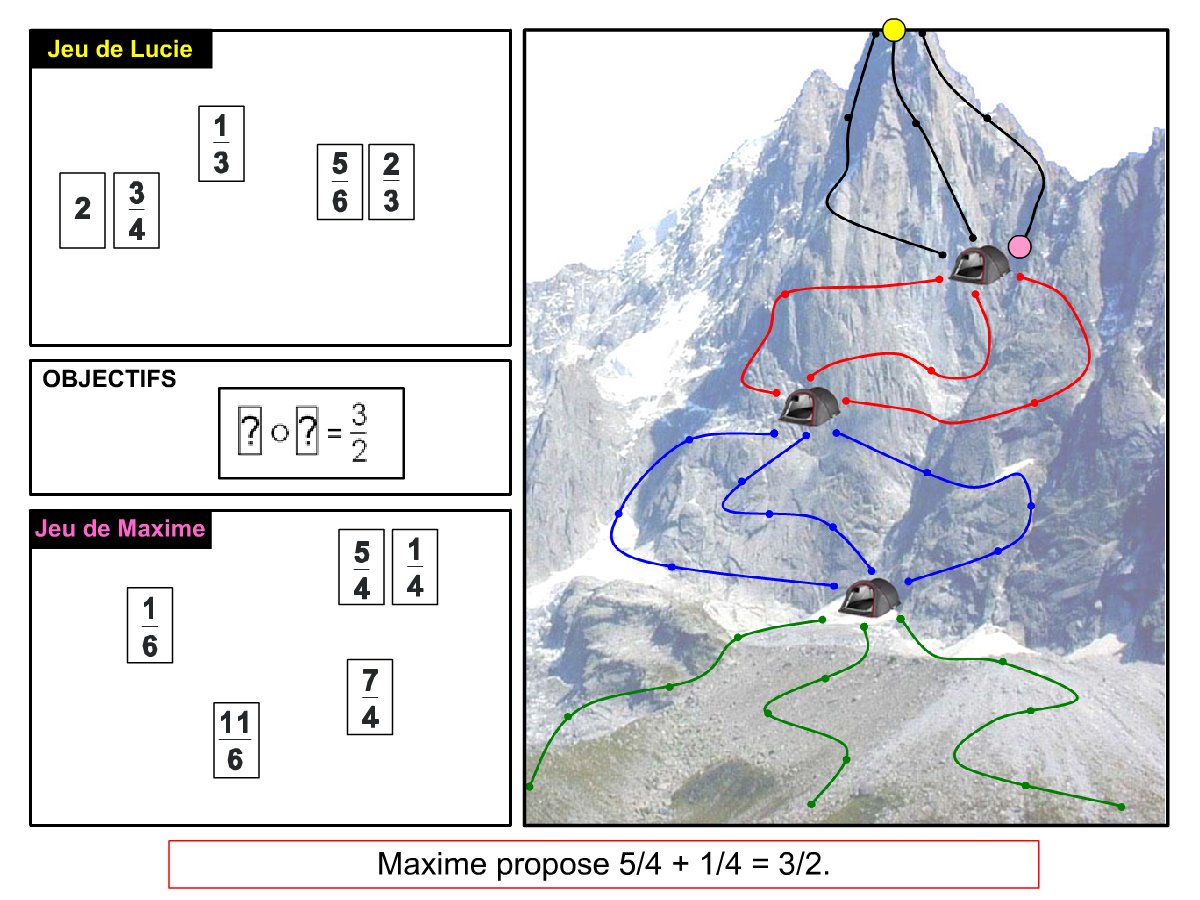
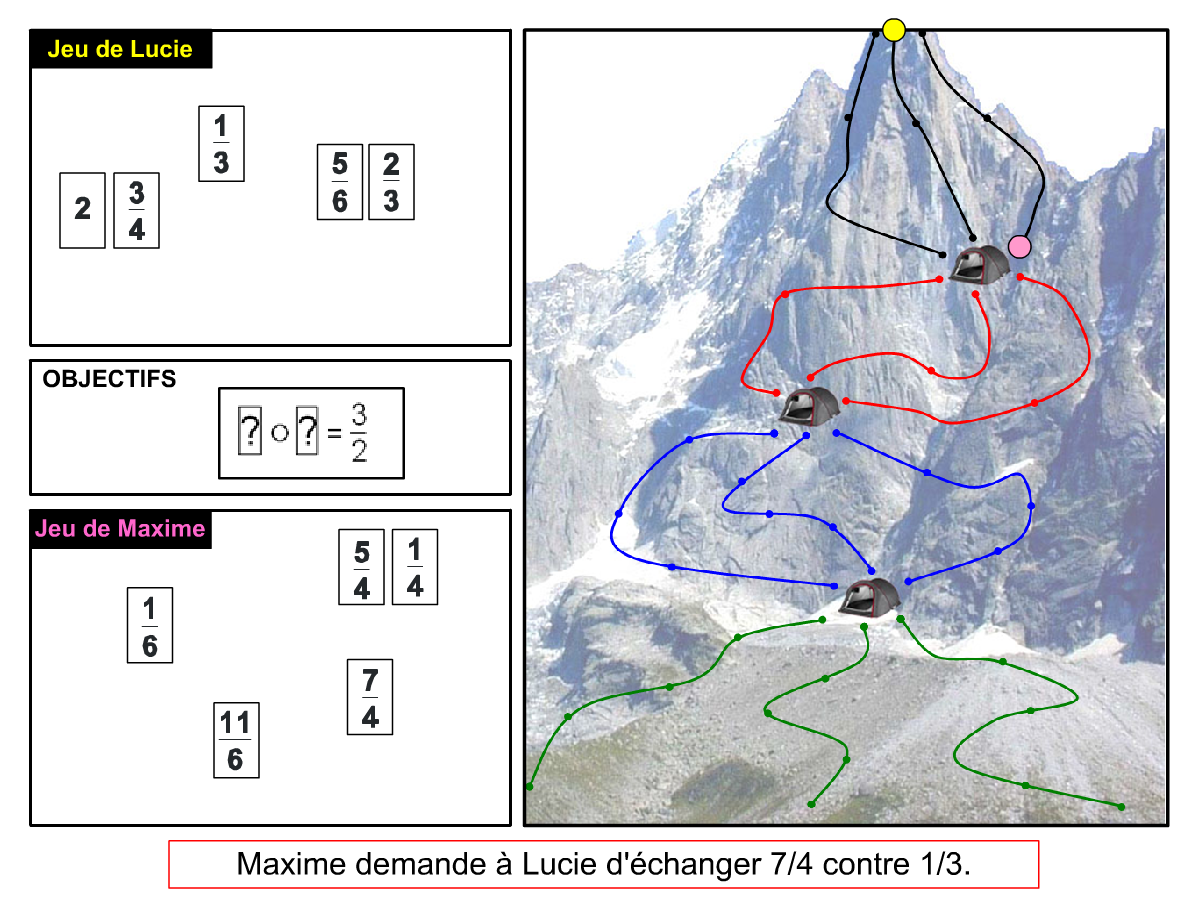
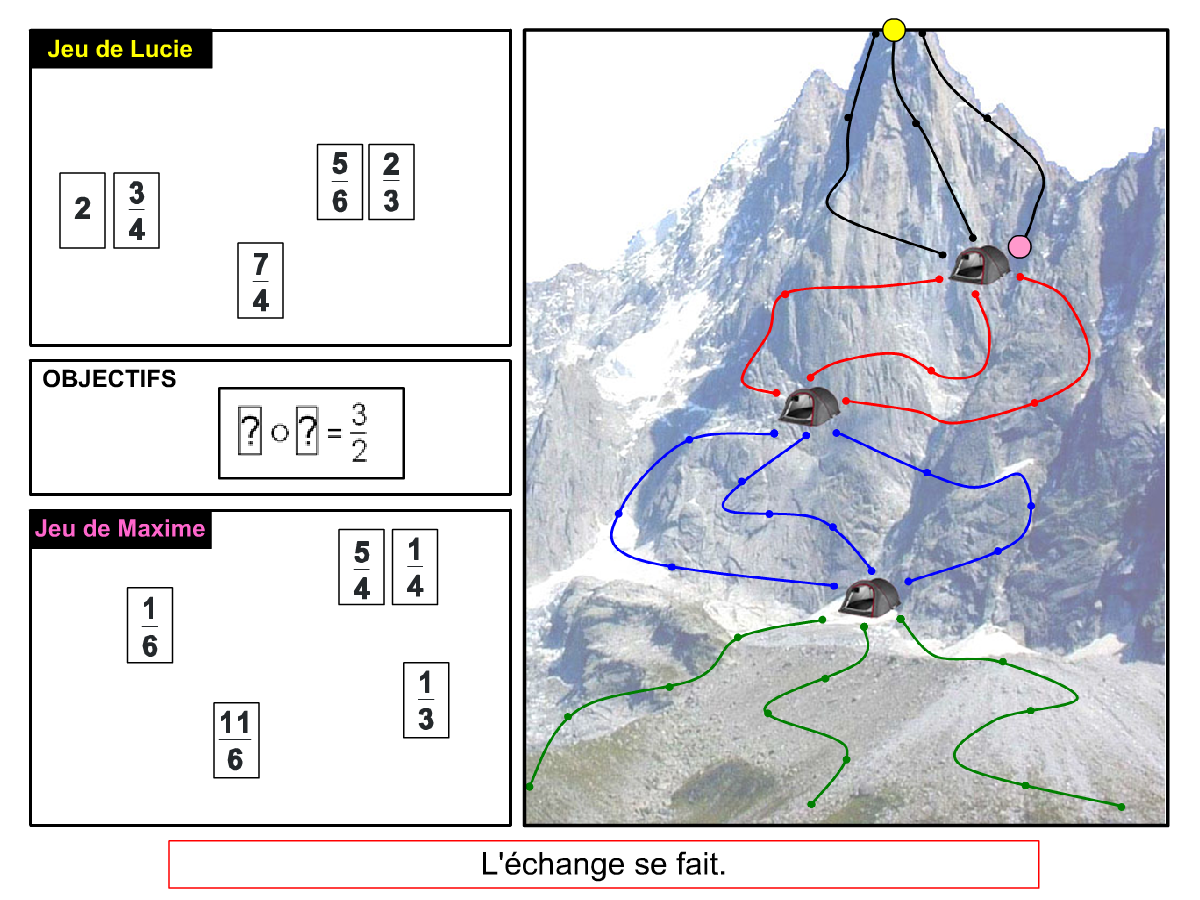
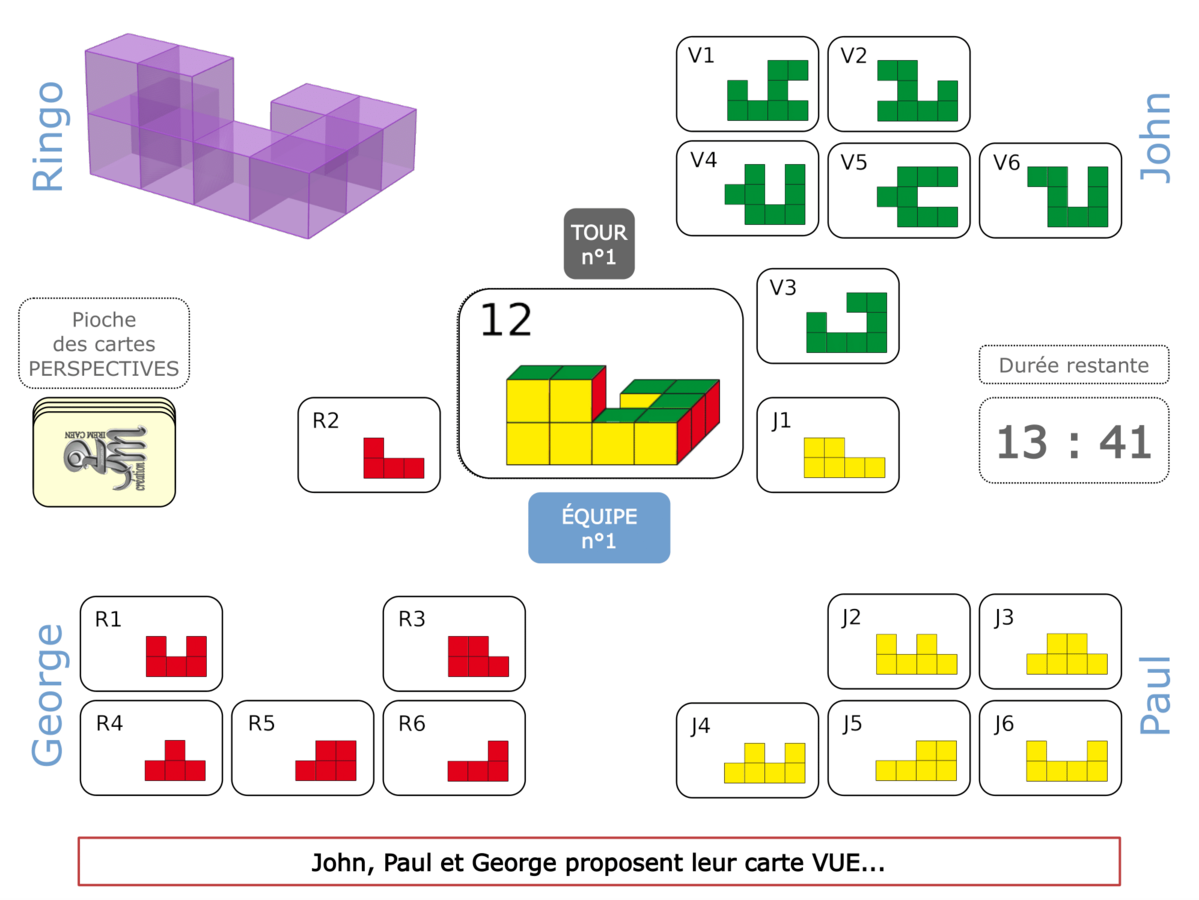
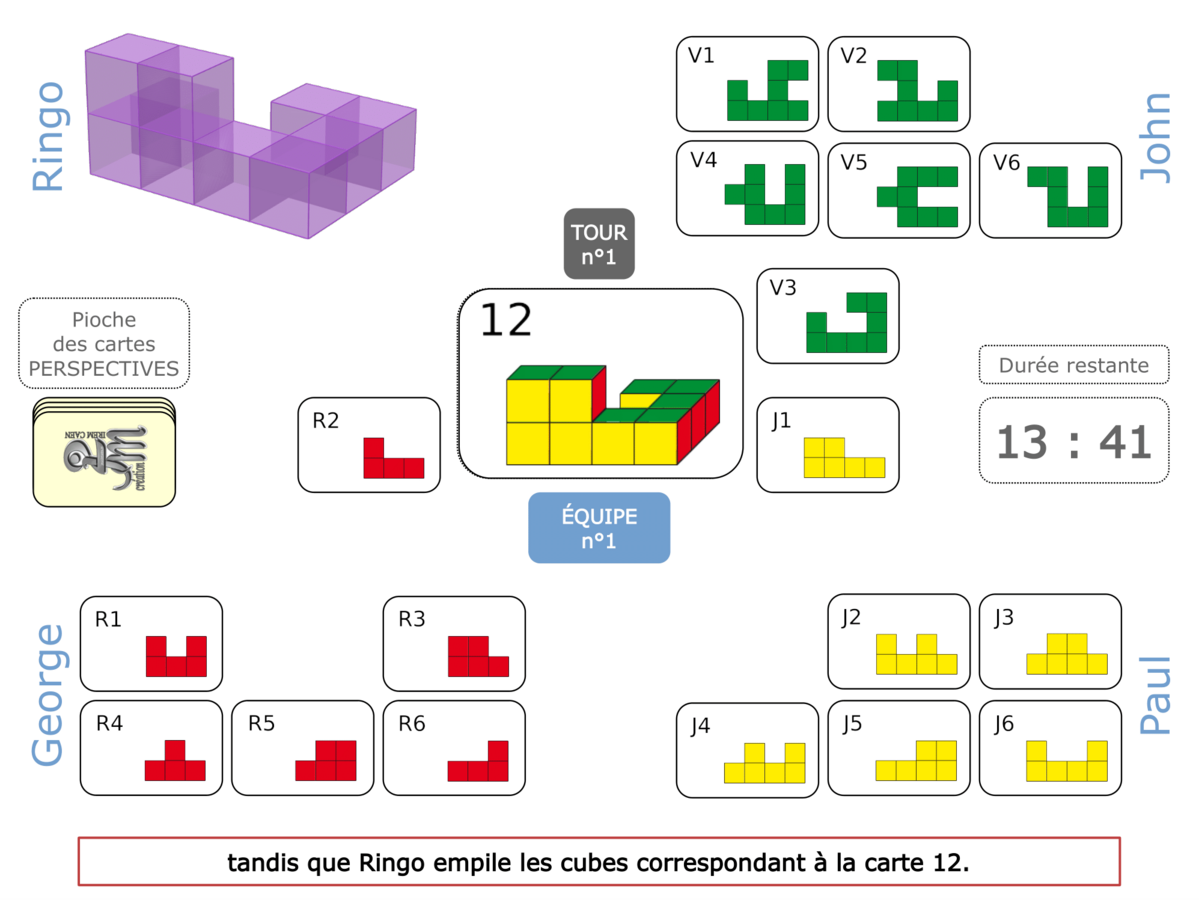
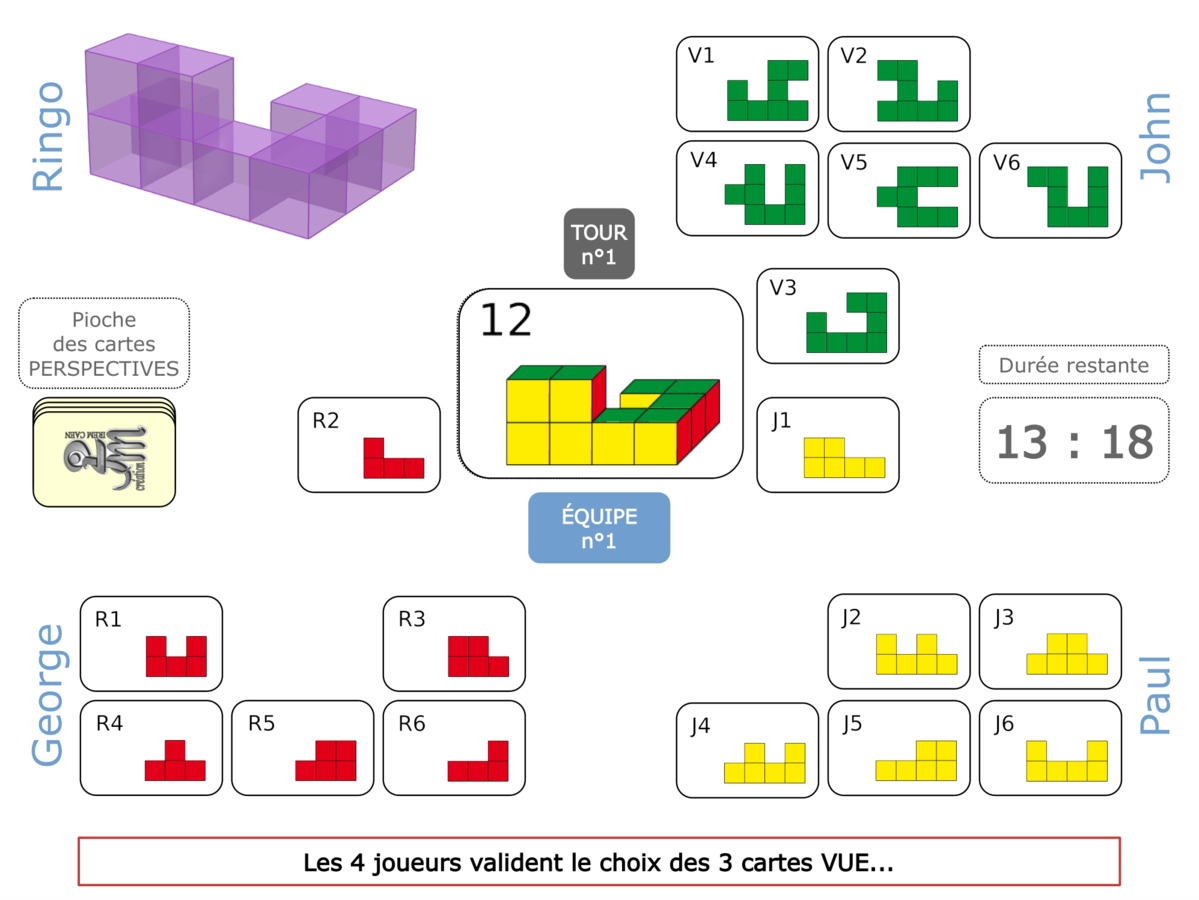
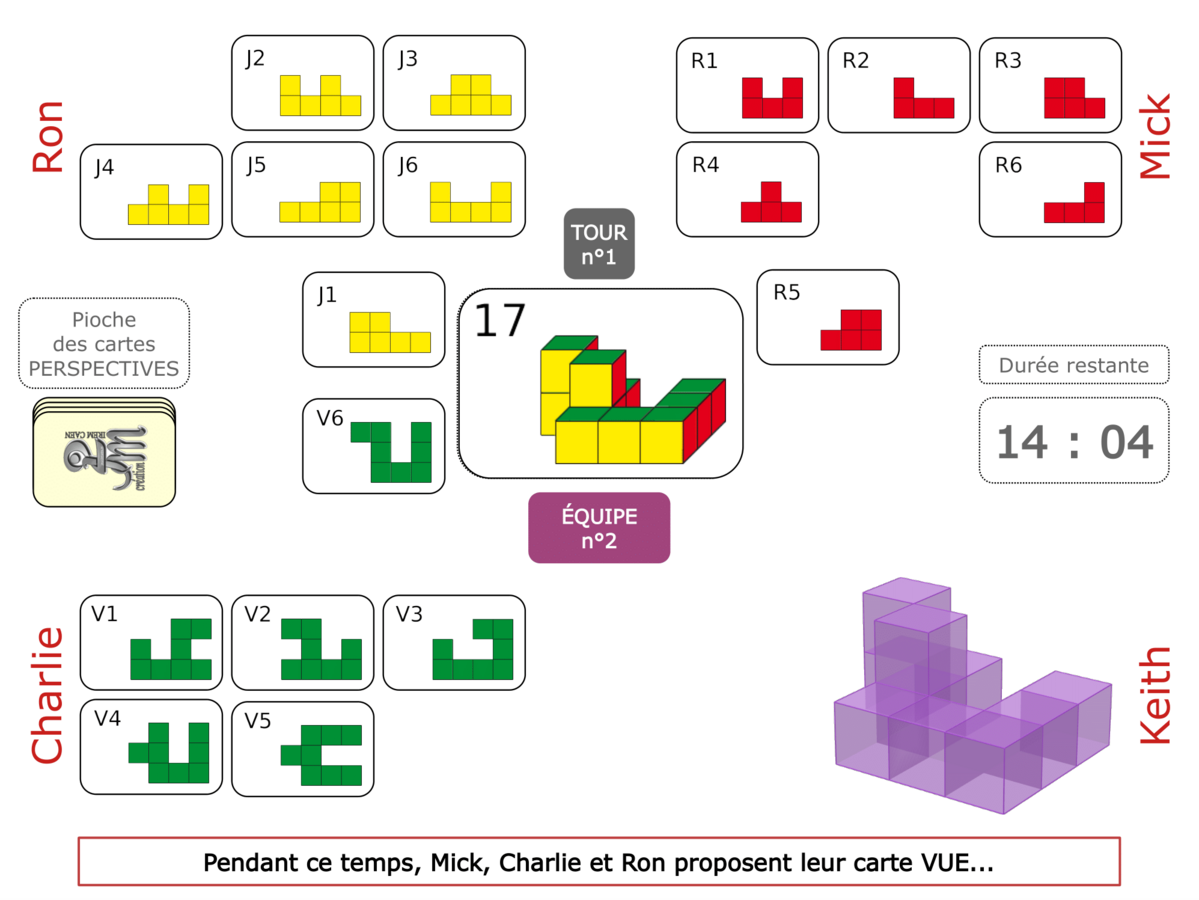
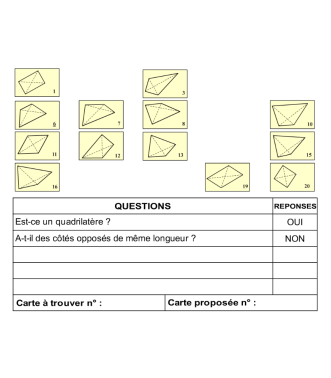
Nous distinguons deux types de jeu : les jeux qui permettent de découvrir de nouvelles notions (les Vectominos), les jeux qui font manipuler des notions en cours d’acquisition (parcours relatif). Il est important que l’enseignant puisse porter un regard critique sur le déroulement des jeux. Nous prévoyons donc une phase écrite qui nous permet de visualiser le déroulement des parties et d’en corriger les éventuelles erreurs. Les élèves sont ainsi en mesure de valider leur niveau de performance.
Intérêt pédagogique du jeu
Il est évident que l’intérêt premier du jeu est de placer l’élève dans une situation motivante du fait de son aspect ludique. Le but poursuivi n’est pas de résoudre un problème, répondre à une question ou faire une démonstration, il est d’atteindre un but fixé par le jeu lui-même qui n’est pas d’ordre mathématique, et les moyens d’y parvenir, même s’ils mettent en jeu des notions mathématiques ne sont pas de type scolaire. Si la motivation a de l’importance pour que les élèves ne s’ennuient pas à l’école, elle ne mérite pas à elle seule que l’on accorde au jeu autant d’intérêt. D’autres aspects, propres à développer des capacités chez les élèves peuvent nous induire à leur donner une plus grande part dans notre enseignement.
Socialisation
Les programmes font un large écho à la socialisation des élèves, au développement du citoyen. Pratiquer un jeu en groupe met en situation de confrontation différentes personnalités qui doivent communiquer, échanger, s’entendre et se respecter, qui doivent être capables d’admettre leurs erreurs ou de convaincre l’autre. Le respect de règles inhérentes au déroulement du jeu sont formatrices pour l’élève qui sera amené dans sa vie d’adulte à appliquer divers règlements dans le domaine social ou professionnel.
Développement de l’esprit
La pratique du jeu nécessite le plus souvent des qualités d’ordre et de méthode, elle impose une réflexion sur la stratégie à adopter, sur l’analyse de la situation, et demande concentration et attention pour progresser le plus efficacement possible. Nous avons tous pu constater que de nombreux enfants et adolescents sont capables d’attention et de concentration sur des jeux (vidéos par exemple !) alors qu’en classe le moindre événement peut détourner leur attention de la tâche sur laquelle ils devraient être fixés. Les jeux que nous avons testés en classe nous confortent dans l’idée que les élèves peuvent rester concentrés sur une tâche, bien au-delà de ce qu’ils sont capables de faire dans des activités plus conventionnelles.
Pratique des notions mathématiques
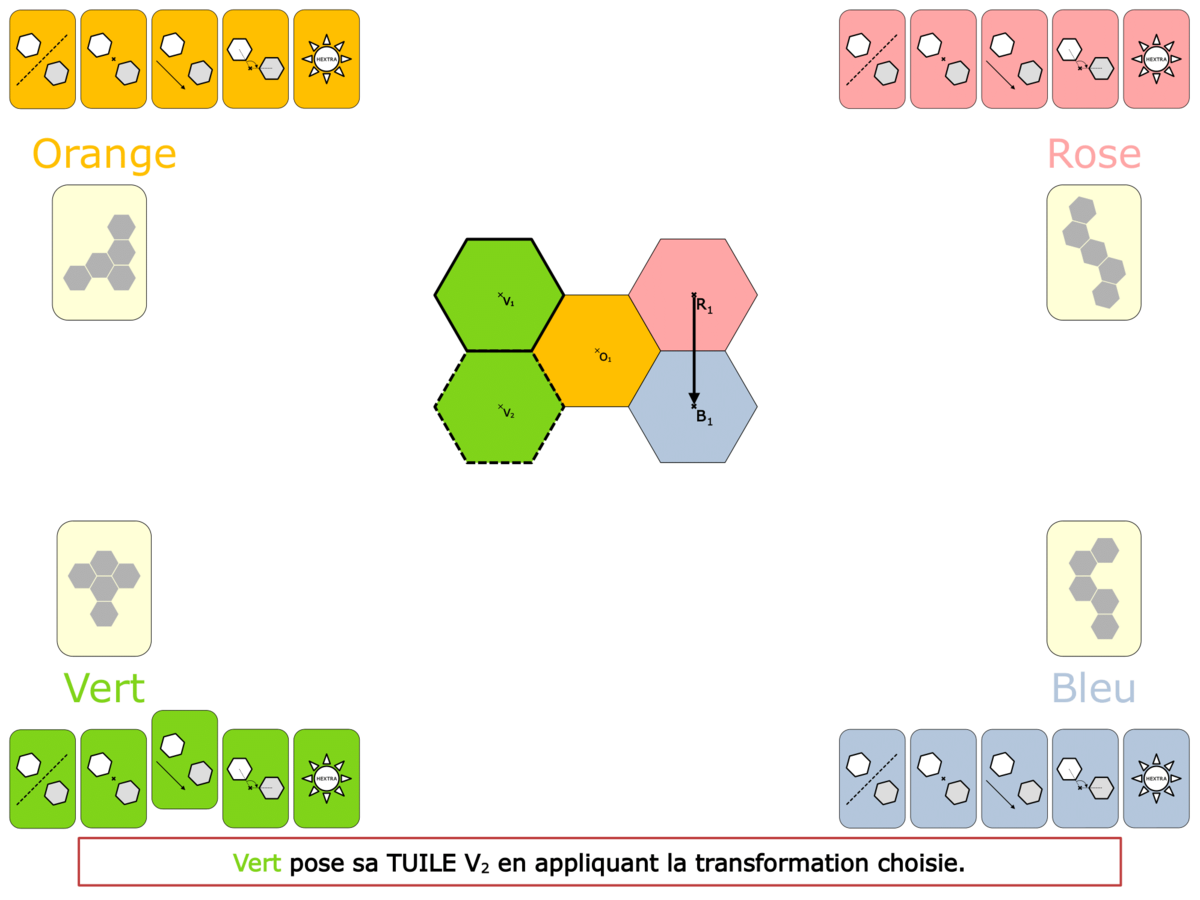
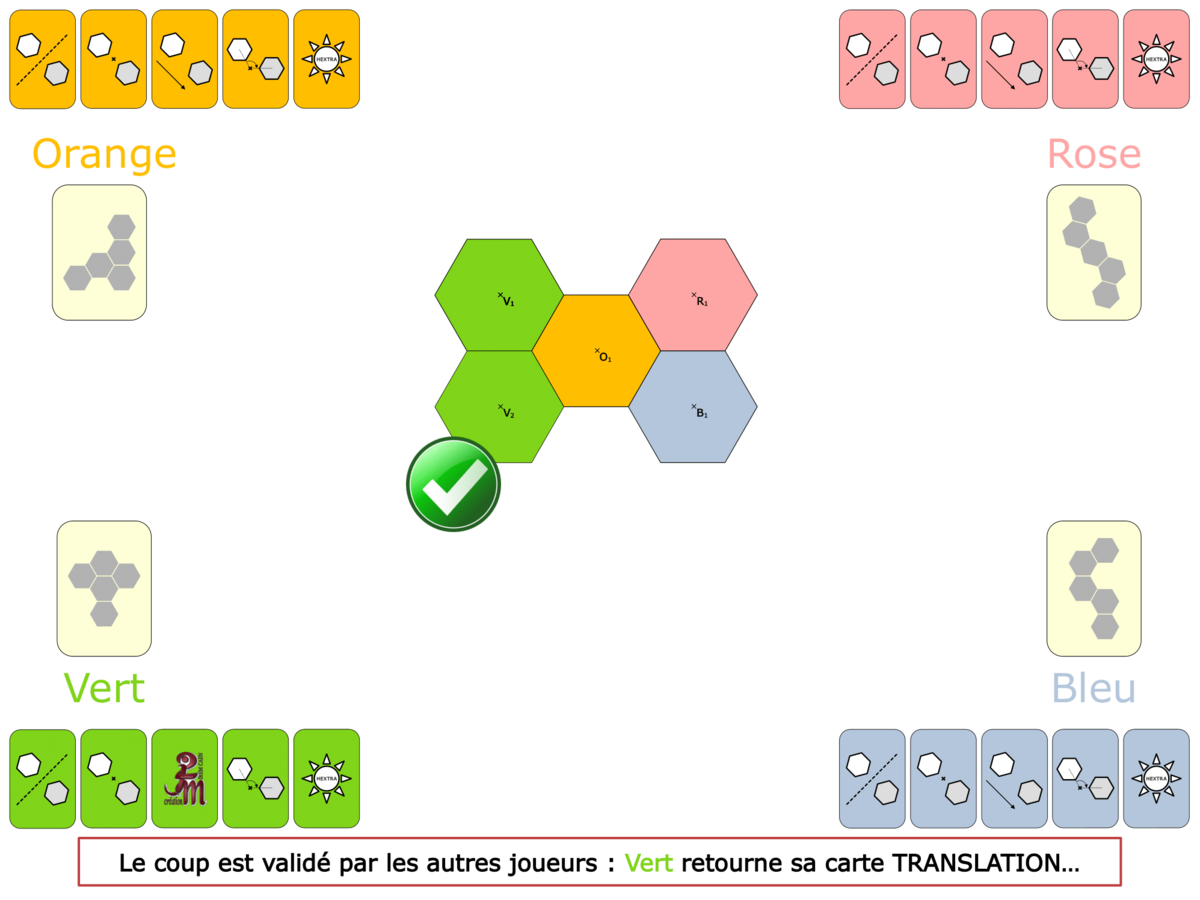
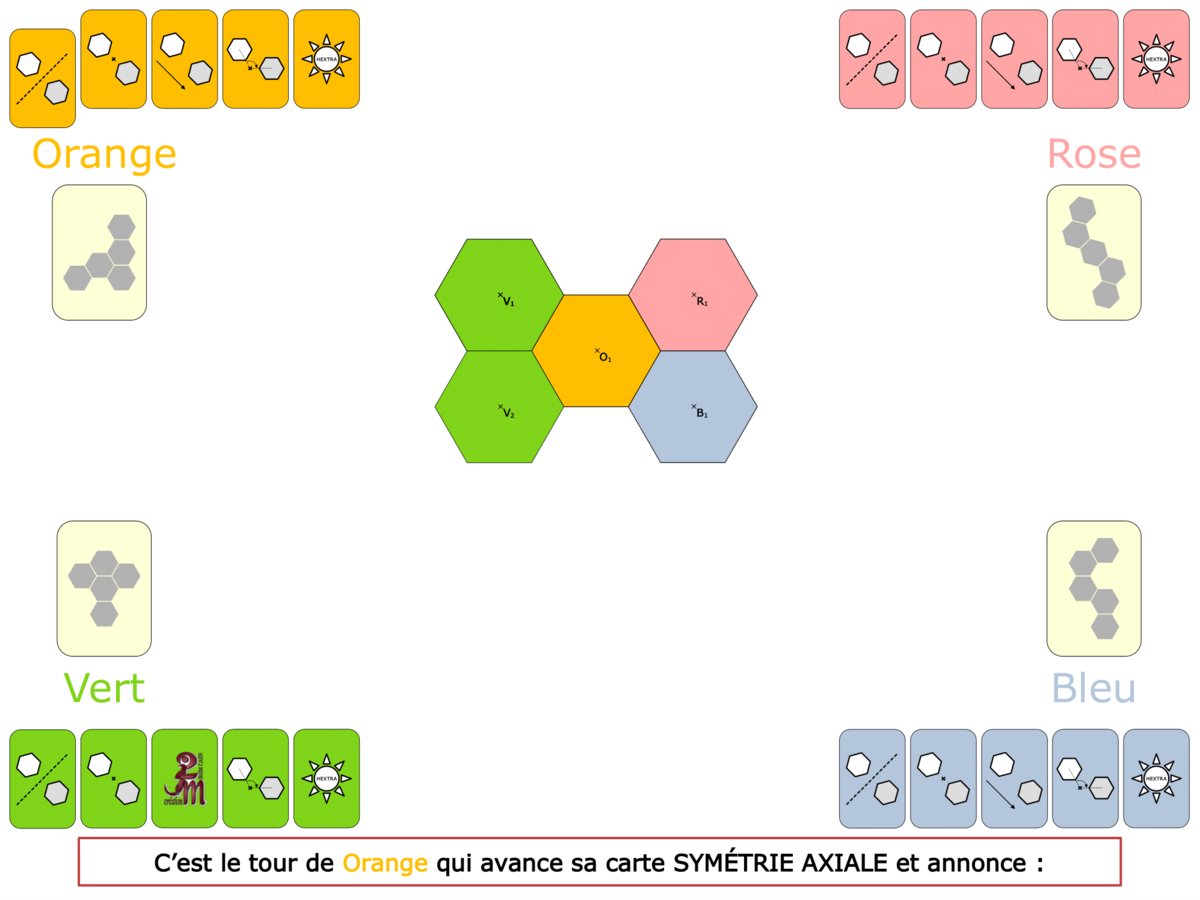
Dans les jeux tels que nous les concevons, il y a répétition de l’utilisation d’un outil mathématique. Chaque «coup» joué faisant fonctionner le savoir visé, le jeu a alors une fonction d’entraînement, d’exercice, sans phénomène d’usure (une heure de pratique des Vectominos fera effectuer à chacun une cinquantaine d’additions ou soustractions de vecteurs) et comme chaque partie est différente, l’intérêt des élèves reste intact. La même tâche, sur un exercice scolaire, serait bien rébarbative et découragerait les plus téméraires !
Nous ne disposons pas d’outils nous permettant d’évaluer de façon significative les progrès réalisés par nos élèves sur les notions abordées par les jeux que nous avons développés. Seule une évaluation réalisée sur les Vectominos nous avait amenés à constater une amélioration sensible de la capacité des élèves à additionner les vecteurs.
Cependant notre expérience riche d’une vingtaine d’années de pratique nous convainc, sans en avoir la preuve formelle, que l’effet jeu se fait sentir sur les autres notions. Par exemple, une allusion faite au jeu au cours de la séquence peut déclencher une correction de procédures erronés chez les élèves. Cela nous incite à penser que les jeux deviennent des activités de référence propres à modéliser ou mémoriser plus efficacement des processus mathématiques.
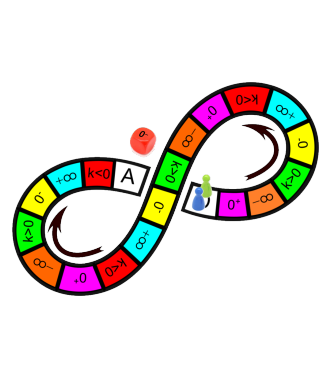
Que l’on soit bien d’accord, nous ne prônons pas «le jeu à tout prix», mais une utilisation parcimonieuse et ciblée sur des notions qui posent problème (par exemple la somme de vecteurs) ou pour lesquelles un entraînement important est nécessaire (comme pour les opérations sur les relatifs). L’apprentissage ne saurait être exclusivement ludique et nécessite des phases de travail strictement scolaire, mais le jeu est l’occasion de faire des maths sans s’en rendre compte et, en imposant une certaine répétitivité, a la faculté de faire fonctionner des outils mathématiques dans le but d’en améliorer la maîtrise. Si de surcroît, il offre une efficacité plus grande qu’une activité classique, nous aurions tort d’en priver nos élèves.
Bons JEUX2MATHS !

Recommandations
Voici quelques consignes de base qui vous permettront de gérer la séance de jeu de façon à ce qu’elle entre dans le cadre de votre expérimentation. Elles ne concernent que des aspects pratiques, et ne retirent en rien votre liberté pédagogique.
Avant la séance
Bien entendu, il vous faudra confectionner le matériel en quantité suffisante si vous souhaitez faire jouer tous les élèves de la classe en même temps, ce que nous recommandons. On pourra utiliser des feuilles de couleurs différentes pour les 7 ou 8 exemplaires nécessaires.
La salle de classe peut être préparée en configuration de jeu, en disposant les tables pour des groupes de 3 ou 4 joueurs.
Il est important de bien anticiper le tout début de la séance, dix minutes maximum au bout desquelles les élèves doivent être installés, le matériel distribué, les règles expliquées et les feuilles de marques données à chaque groupe.
Pendant la séance
Dans les premières minutes de la mise en route, il est également important d’expliciter le contrat didactique : la séance de jeu fait partie intégrante du cours de mathématiques, elle a une part importante dans l’apprentissage des notions. Elle n’est en aucun cas une récréation, et les notions abordées seront reprises et approfondies dans la suite de la séquence.
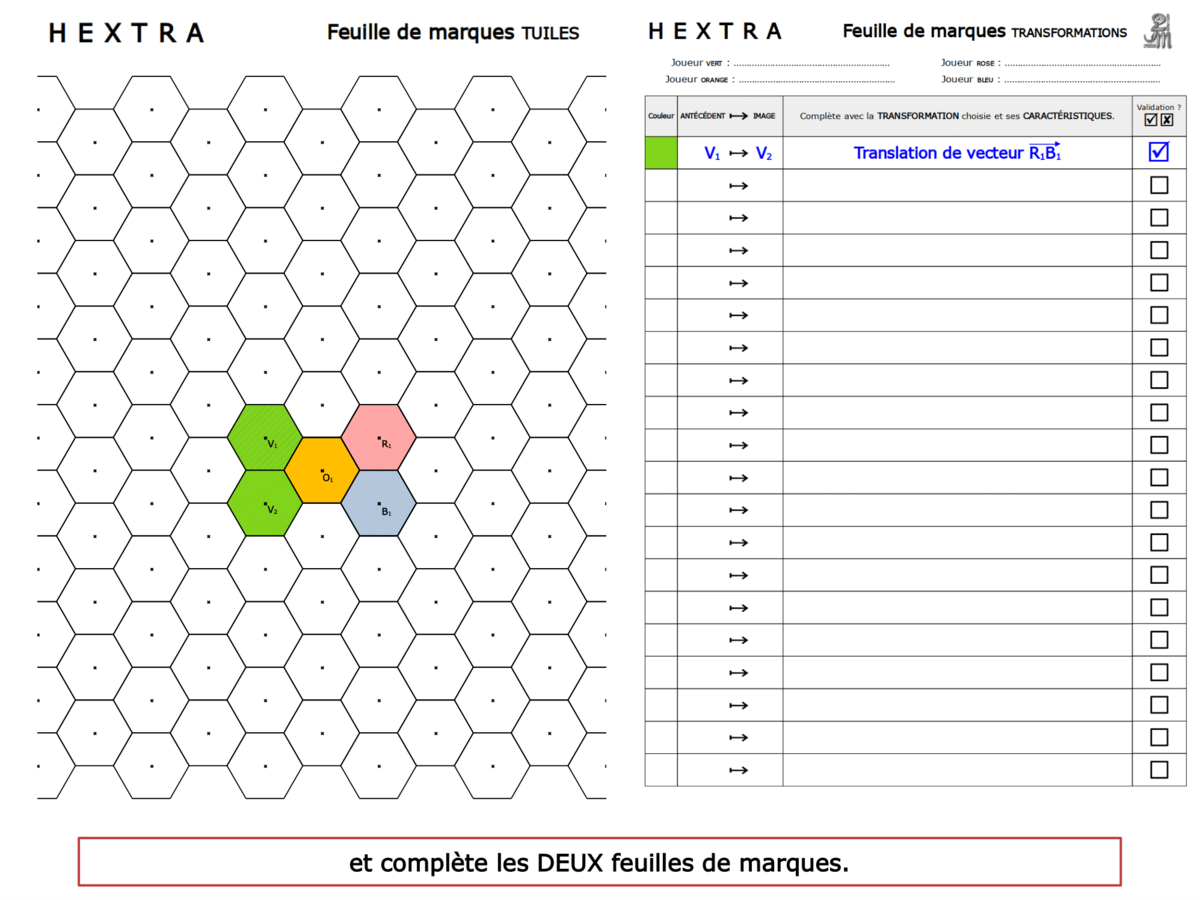
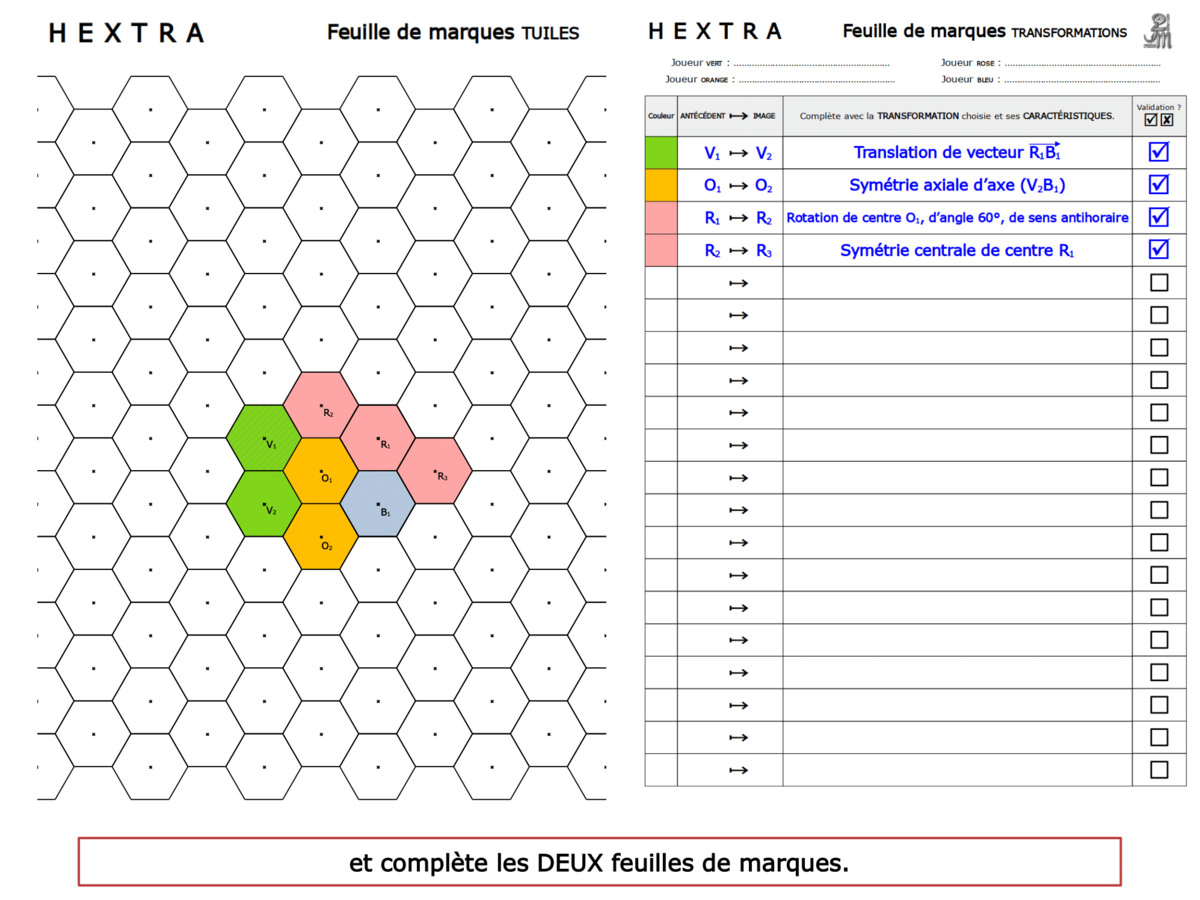
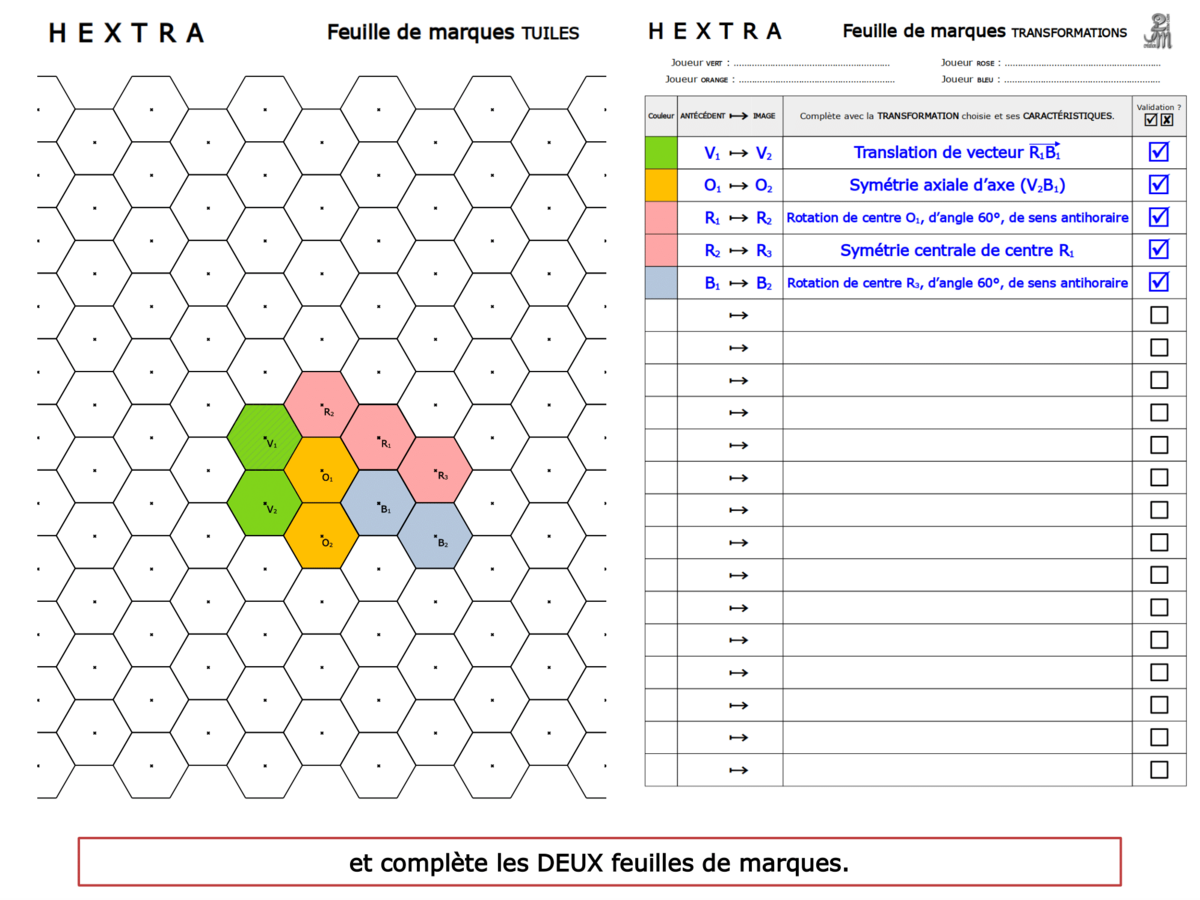
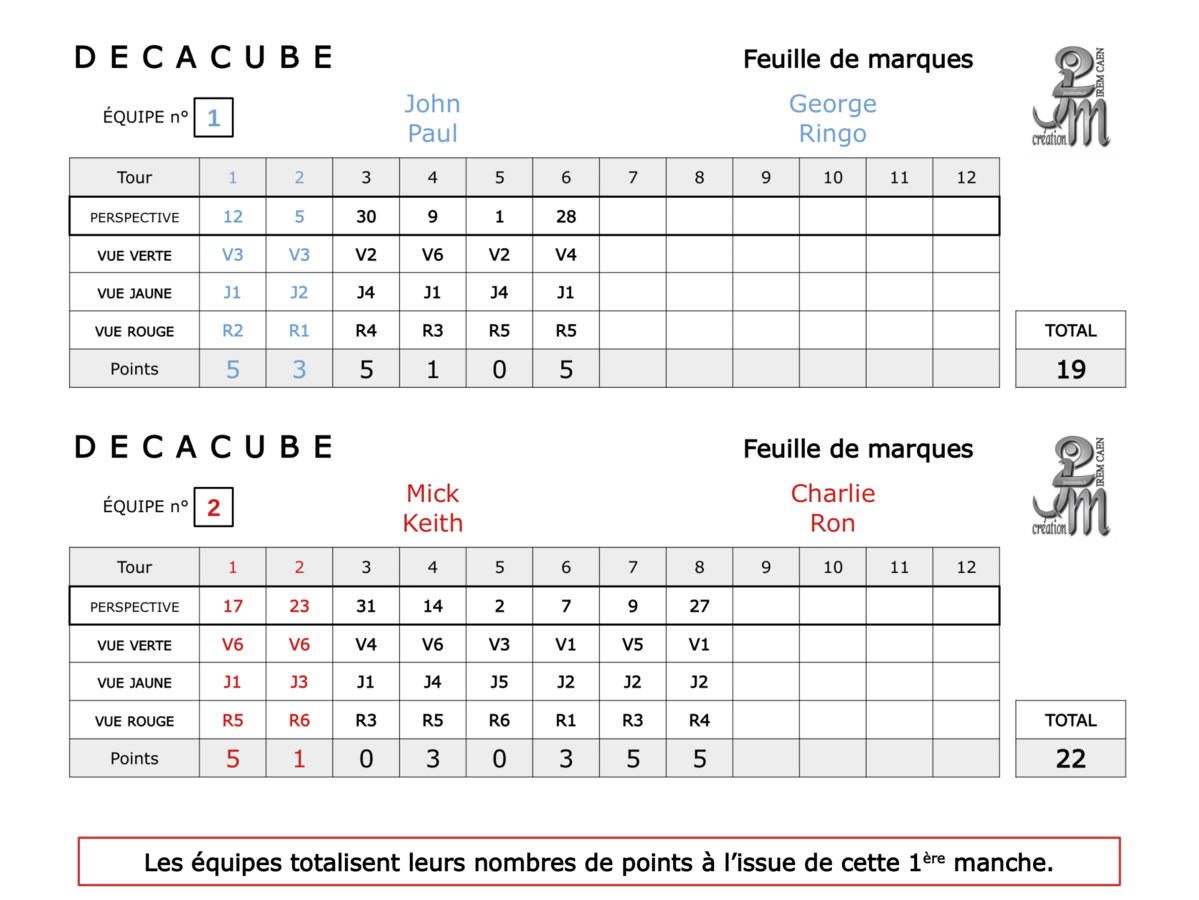
Le professeur donne à chaque groupe une feuille de marque sur laquelle les élèves notent chaque coup au fur et à mesure de la partie. Cette feuille, ramassée par le professeur, permet un contrôle sur l’activité mathématique des élèves, permet aux élèves de formuler leur coup mathématiquement, et servira à la séance suivante de retour sur les éventuelles erreurs.
Il est bon d’expliquer tout cela aux élèves afin qu’ils saisissent les enjeux de l’activité.
Activité du professeur pendant la séance
Il a un rôle d’animateur au début de la séance, puis d’arbitre pendant la phase de jeu. Les groupes d’élèves doivent s’auto-réguler, gérer seuls leurs décisions de jeu. Le professeur n’intervient que pour rappeler les règles du jeu et/ou seulement en cas de conflit important.
Fin de la séance
Pensez au temps qu’il faut pour ramasser et vérifier tout le matériel, ramasser les feuilles de marques et donner le travail à faire à la maison !
Bons JEUX2MATHS !

Enrichissements et Prolongements
Dans notre démarche d’utilisation des jeux en classe, notre objectif est de faire en sorte que le jeu fasse partie intégrante de la démarche pédagogique. Le jeu n’est pas une parenthèse ludique proposée aux élèves pour les divertir, mais doit s’intégrer comme activité à part entière dans la séquence d’apprentissage. Il doit donc s’inscrire naturellement dans l’enchaînement des activités de classe.
Nous considérons deux façons de faire en sorte que le jeu soit une activité à part entière, selon que l’on reste dans le jeu (ce sont les enrichissements) ou que l’on dépasse le cadre du jeu (ce sont les prolongements).
Les Enrichissements
Comme leur nom l’indique, les enrichissements donnent une richesse supplémentaire au jeu ; c’est donc dans le cadre même du jeu qu’on les développera. Ils permettent :
* de donner une meilleure efficacité au joueur,
* de donner une nouvelle dynamique au jeu,
* d’aller plus loin dans les domaines méthodologique ou notionnel.
Les enrichissements ne sont pas forcément destinés à tous les élèves de la classe. Ils peuvent être un moyen de différenciation. Les meilleurs joueurs trouveront une nouvelle dynamique de jeu par l’apport de techniques plus efficaces qu’elles soient mathématiques ou méthodologiques.
Les Prolongements
Ils ne sont plus du domaine du jeu, mais utilisent les pièces du jeu ou le mécanisme du jeu pour développer la notion mathématique. Ils permettent :
* d’assurer le lien entre les savoir-faire du jeu et les savoir-faire institutionnels, et donner de ce fait un statut d’activité de référence au jeu,
* de donner vis à vis de l’élève une légitimité mathématique au jeu,
* d’utiliser le jeu comme un élément pédagogique à part entière,
* de profiter de l’aura positive du jeu pour proposer des activités mathématiques de type plus classique en conservant la motivation des élèves.
Les prolongements sont destinés à tous les élèves de la classe. Ils peuvent prendre plusieurs formes (devoirs à la maison, activités de classe…), mais sont destinés à ouvrir les perspectives offertes par le jeu qui, pour des raisons techniques, limite souvent le champ mathématique abordé.
Conception des prolongements
Le but du prolongement étant d’établir un lien entre le jeu et les activités qui vont suivre, il doit rester dans l’esprit du jeu, soit en utilisant les pièces (cartes, pions…) ou le mécanisme (la façon de jouer les coups).
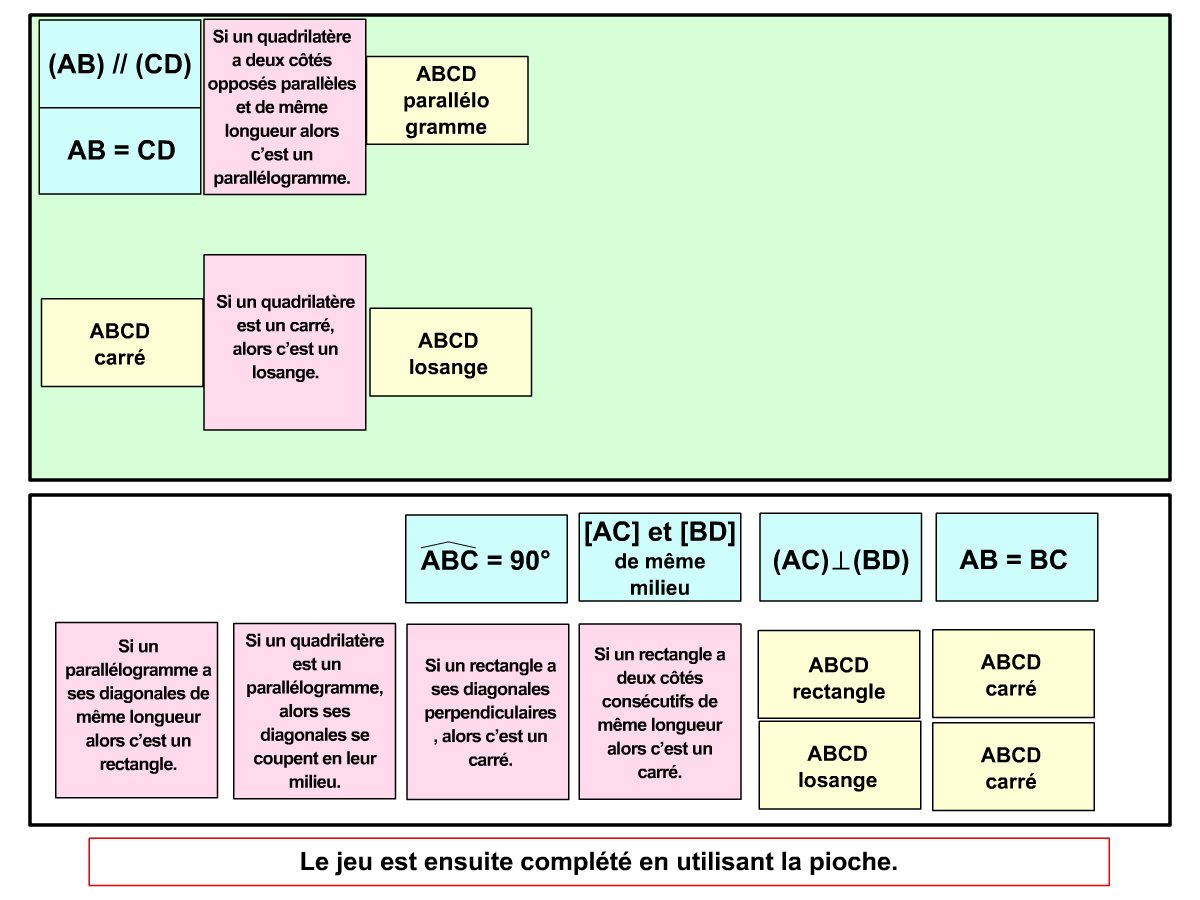
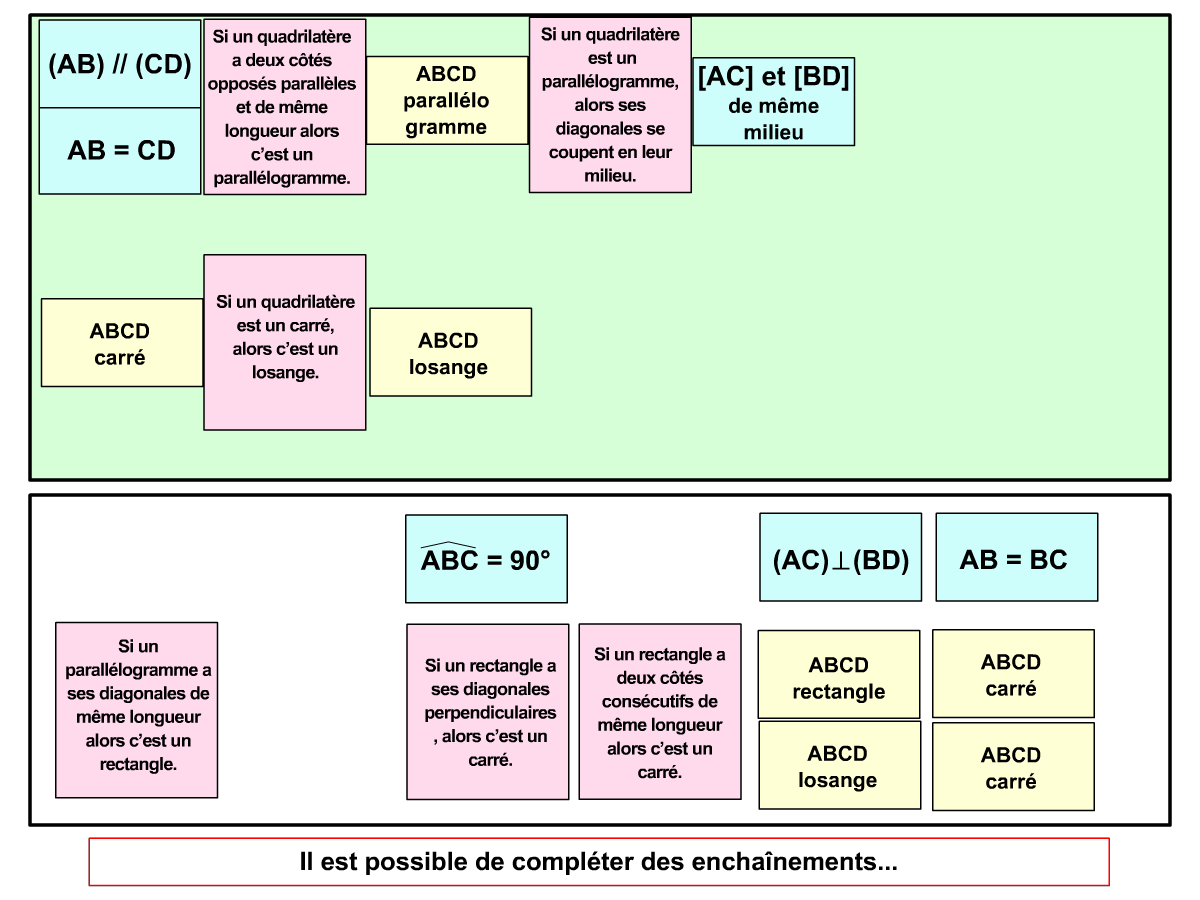
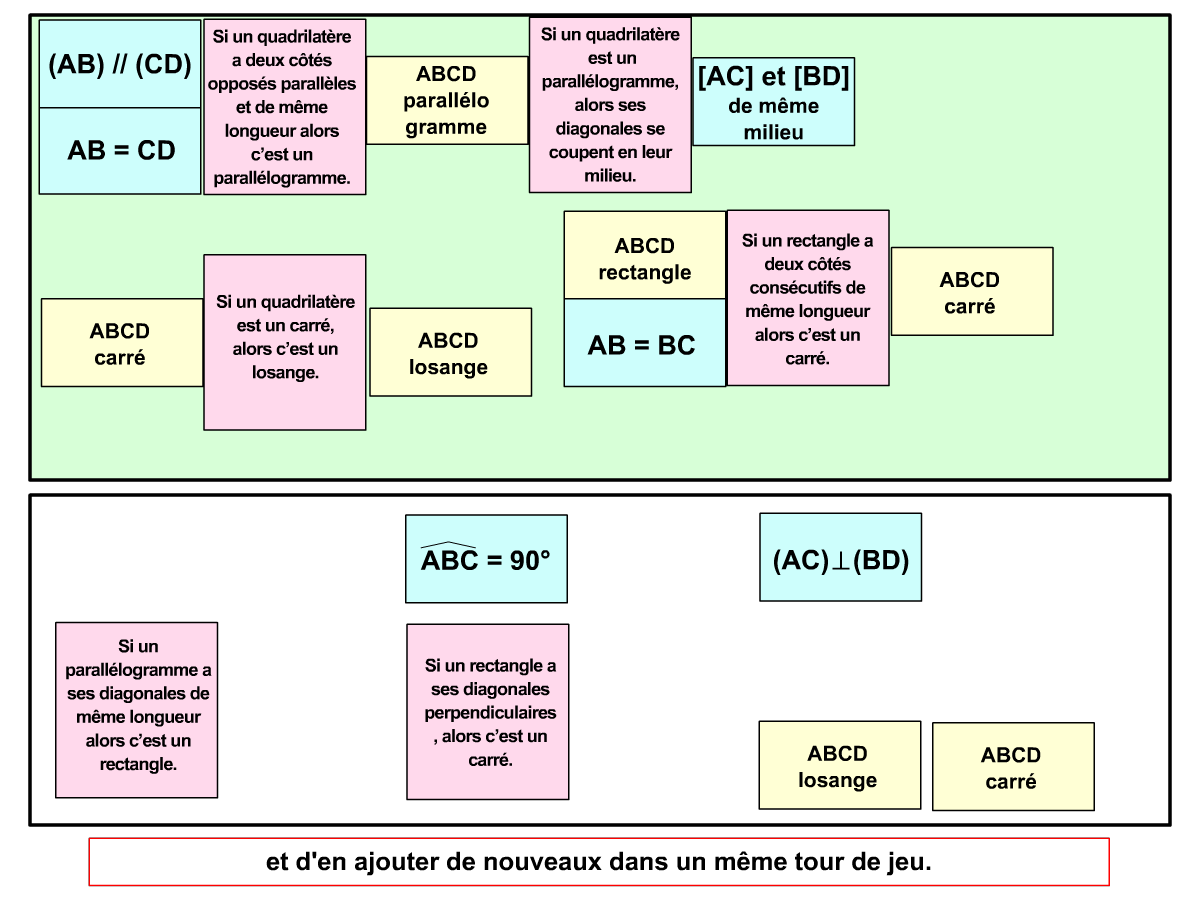
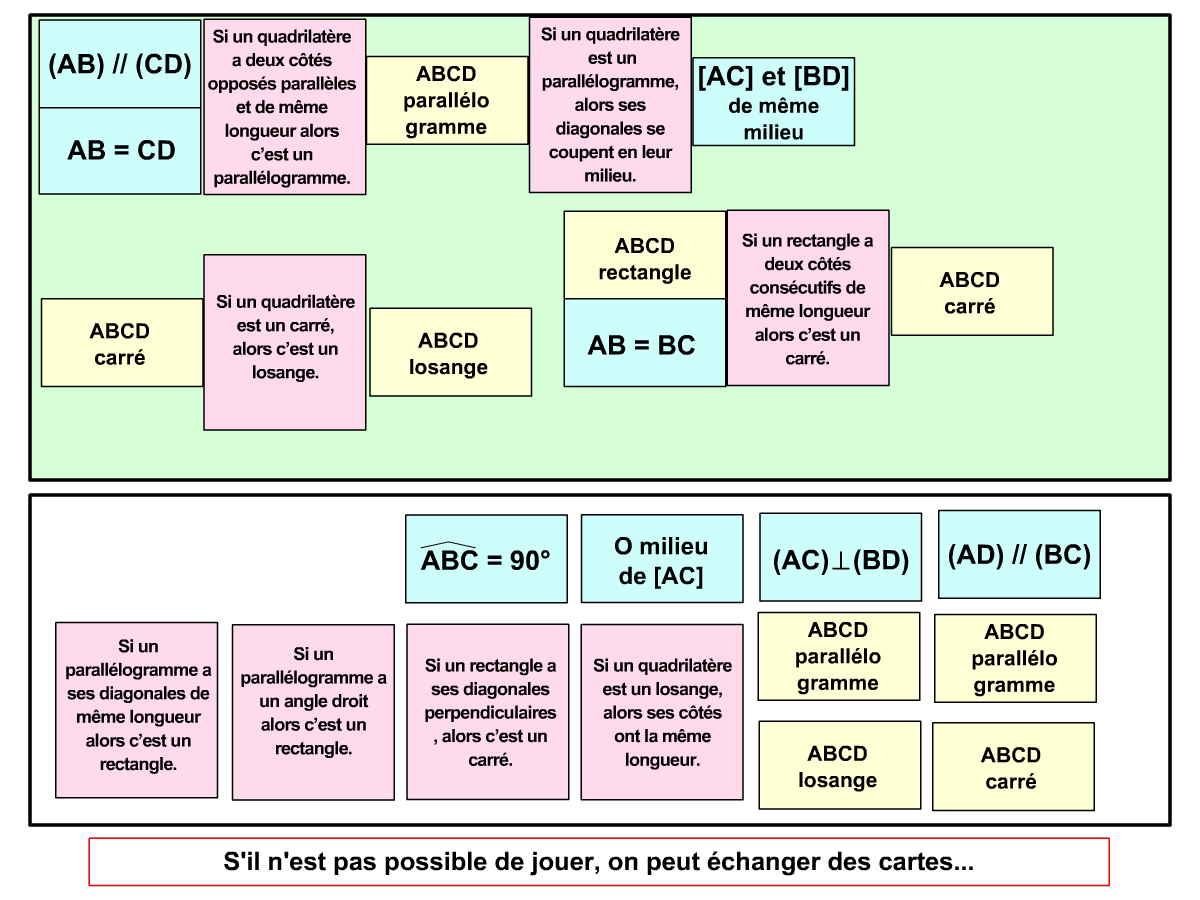
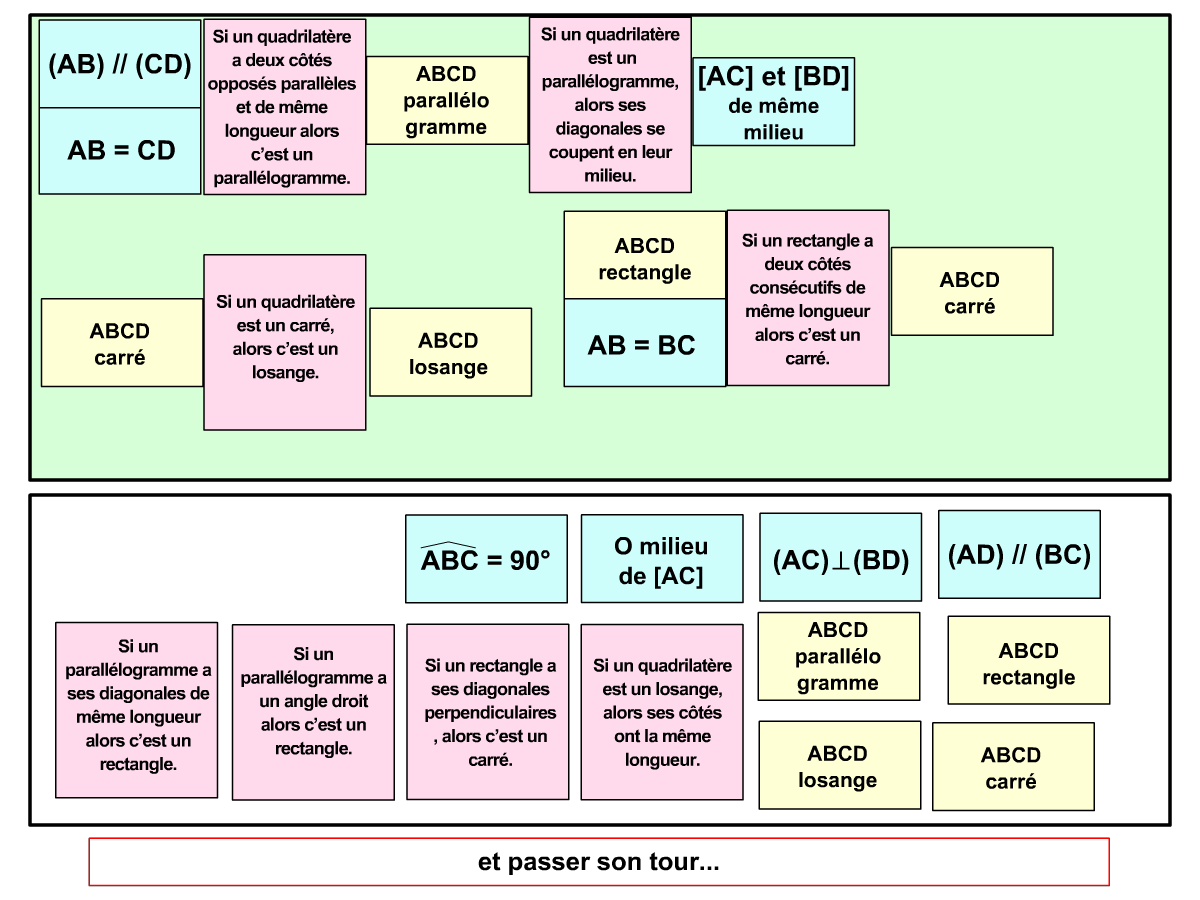
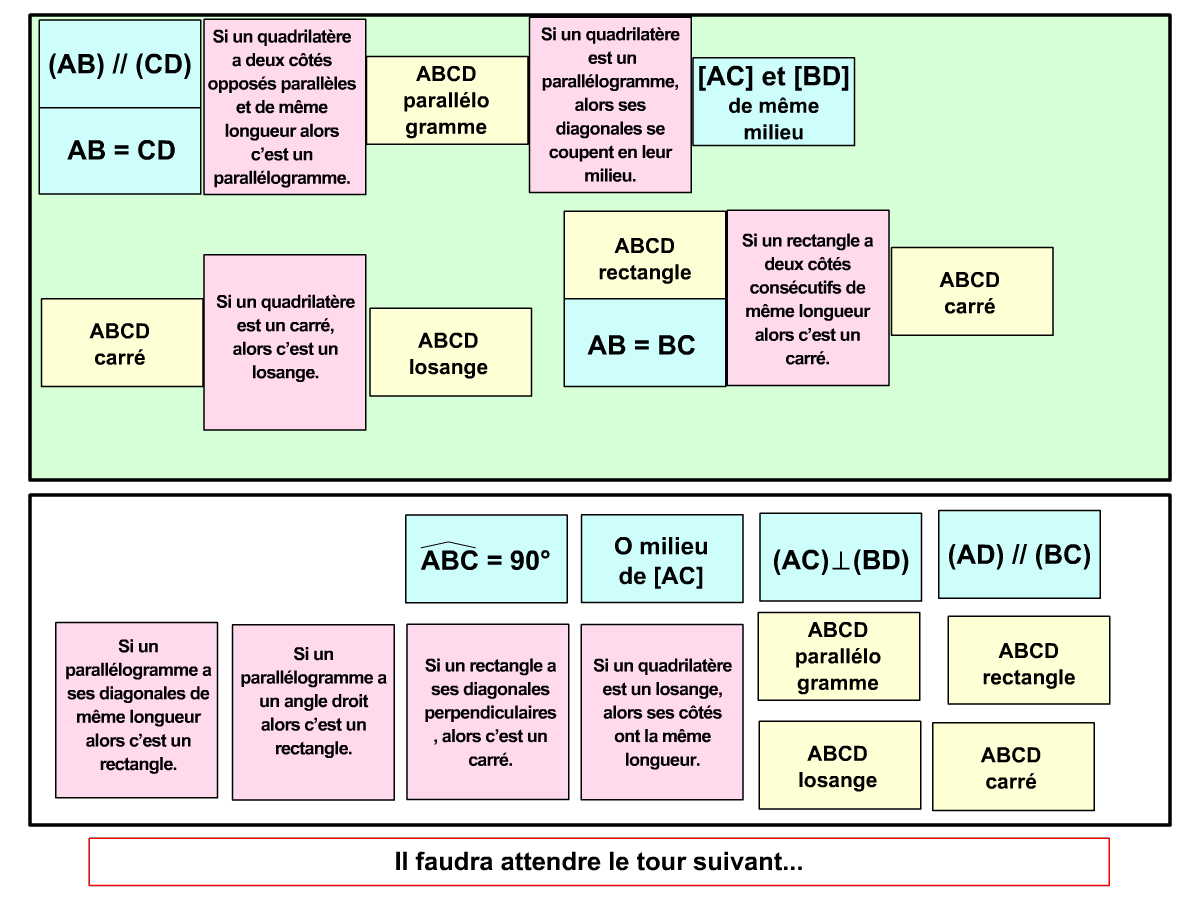
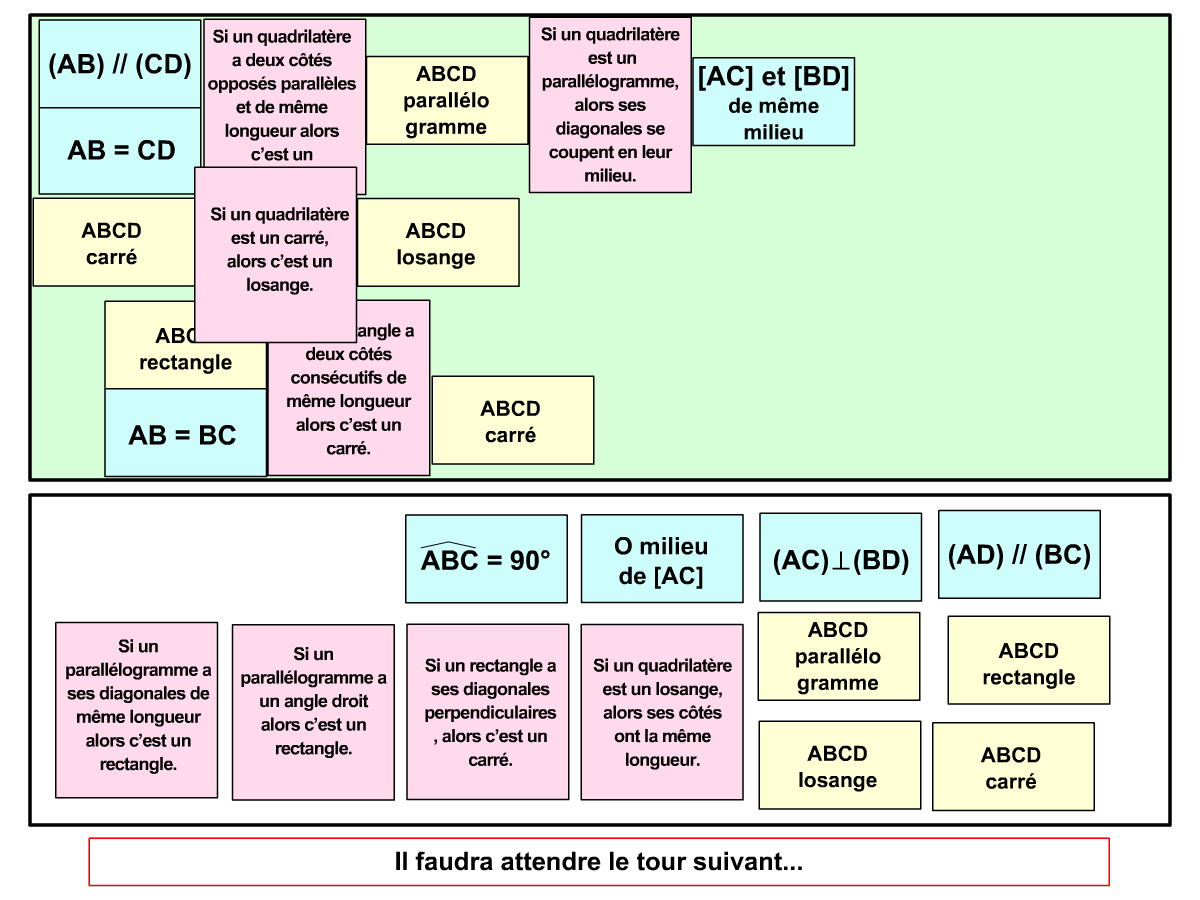
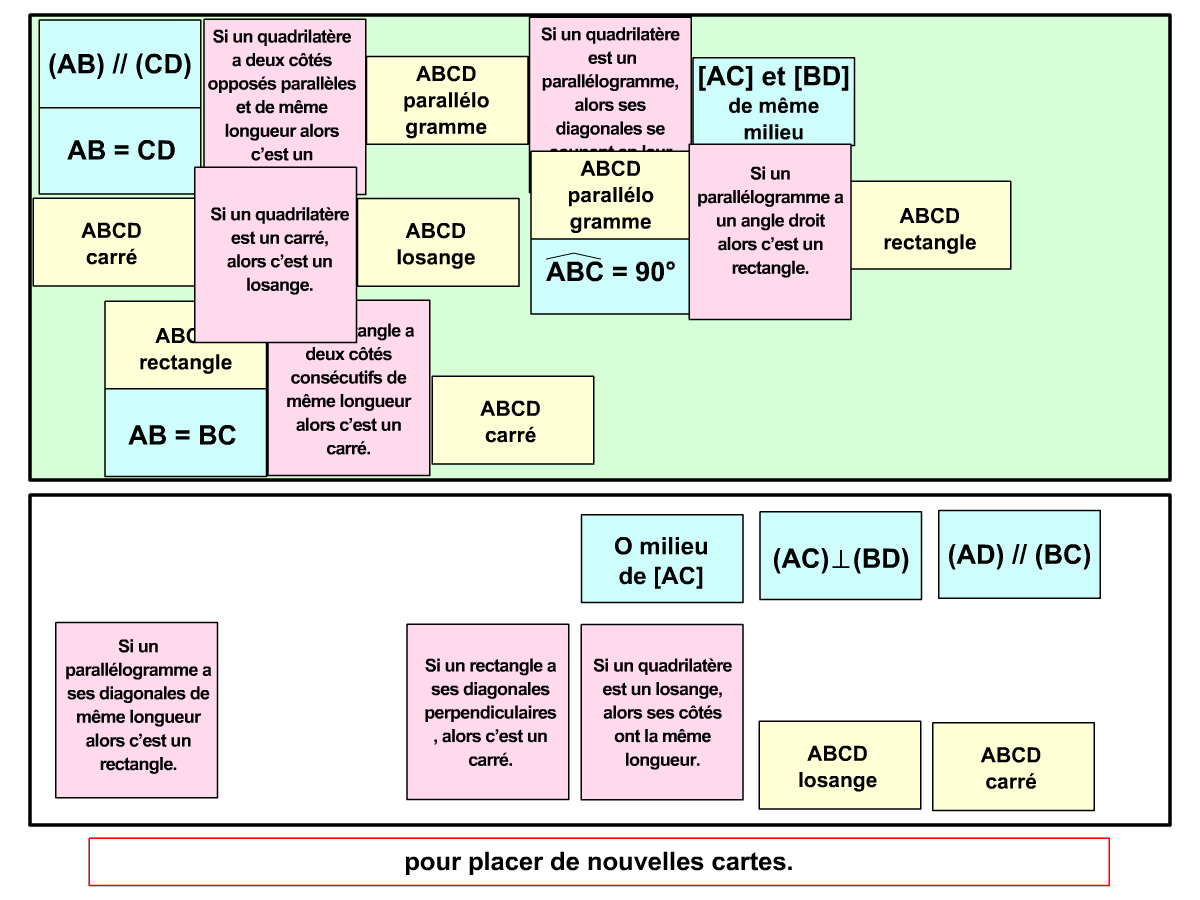
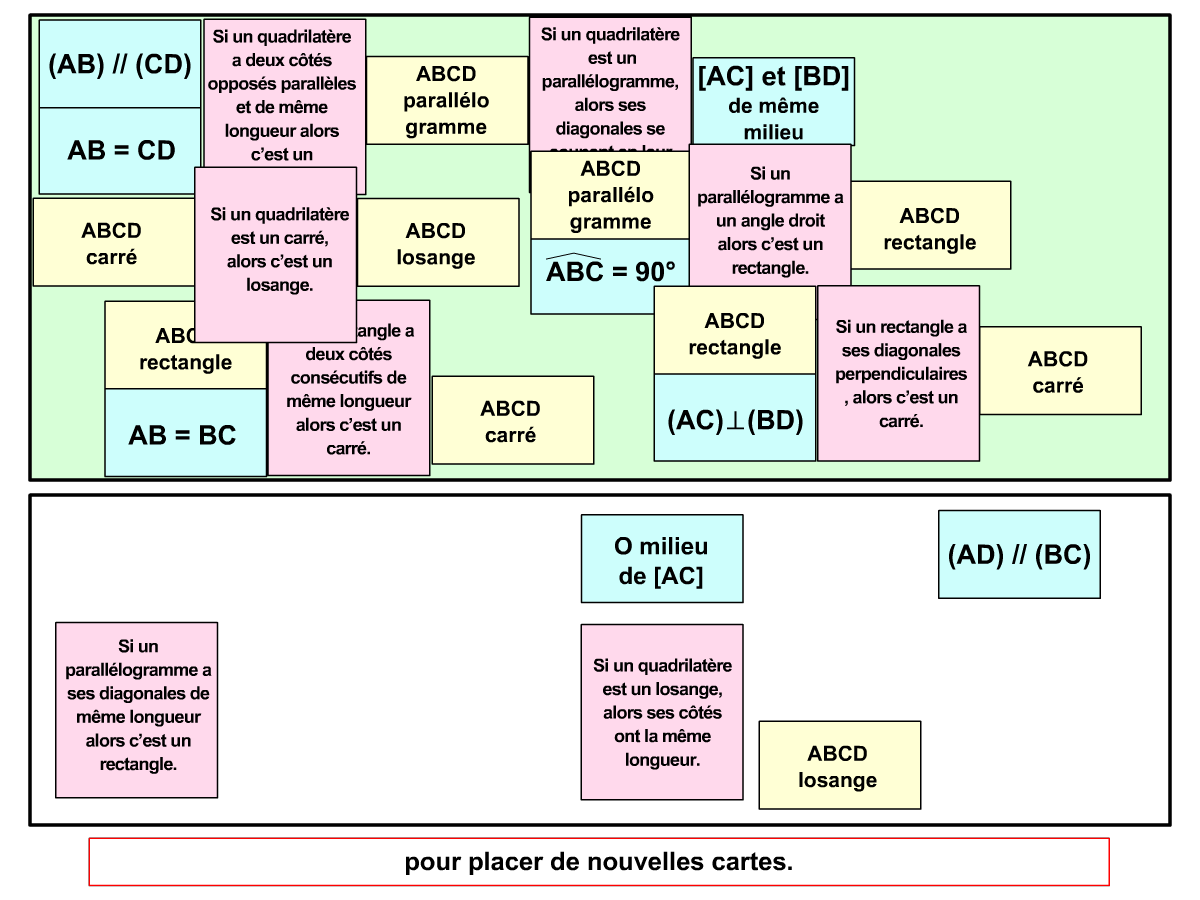
Utilisation des pièces : lorsque les pièces du jeu sont assez variées, on peut les étudier de façon plus approfondie (les propriétés d’une figure par exemple), mener des activités d’ordre méthodologique (organisation des éléments en tableaux) ou encore reproduire à l’aide des instruments pour les jeux à base géométrique. De cette façon les élèves renforcent leurs expérimentations faites pendant le jeu et valident les savoirs abordés.
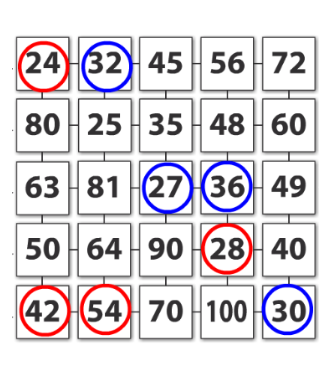
Utilisation du mécanisme : lorsque le jeu limite les savoirs visés en n’utilisant que des éléments simples (Relatron, Multipower, Vectominos), les prolongements permettent d’élargir le champ des valeurs abordées dans le jeu. Le prolongement reprend alors le mécanisme du jeu mais le niveau de difficulté assoit les techniques qui peuvent être acquises dans les cas simples mais dysfonctionner avec des valeurs plus complexes. Dans le cas où le jeu est utilisé pour découvrir une nouvelle notion (Dominato), le prolongement peut permettre de mathématiser le mécanisme du jeu ; l’activité permettra alors l’institutionnalisation d’un nouveau savoir.
Suggestions
Bien évidemment nous sommes ouverts à toutes suggestions que vous jugeriez utiles de nous transmettre. Elles sont les bienvenues quelle qu’en soit la forme : des critiques, des idées d’enrichissements, de prolongements ou même d’amélioration des jeux.
Vos expériences peuvent également nous ouvrir de nouvelles perspectives, n’hésitez pas à nous les raconter, elles pourraient trouver leur place sur le site. Pour ce faire, utilisez la page CONTACT du site.